Koordinat persegi panjang contoh dan latihan diselesaikan

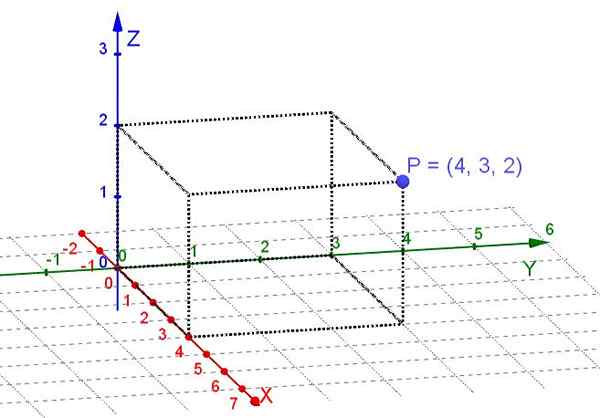
Itu Koordinat persegi panjang o Cartesian adalah yang diperoleh saat diproyeksikan secara ortogonal pada tiga sumbu cartesius x, y, z titik yang terletak di ruang tiga dimensi.

Sumbu cartesius saling berorientasi tegak lurus lurus. Dalam sistem koordinat Cartesian, tiga bilangan real yang merupakan koordinat persegi panjang ditugaskan ke setiap titik di ruang angkasa.

Gambar 1. Koordinat persegi panjang titik P (elaborasi sendiri)

Pesawat adalah subruang dari tiga ruang -dimensi. Dalam hal mempertimbangkan titik pada pesawat, cukup untuk memilih sepasang sumbu tegak lurus x, dan sebagai sistem Cartesian. Kemudian pada setiap titik di pesawat, dua bilangan real ditugaskan kepadanya bahwa koordinat persegi panjangnya.

[TOC]

Asal koordinat persegi panjang

Koordinat persegi panjang pada awalnya diusulkan oleh matematikawan Prancis René Descartes (1596 dan 1650), itulah sebabnya mereka menerima denominasi Cartesian.

Dengan gagasan descartes ini, titik -titik bidang dan ruang diberi bilangan, sehingga angka geometris telah mengaitkan persamaan aljabar dan teorema geometris klasik dapat ditunjukkan secara aljabar secara aljabar. Dengan koordinat cartesian, geometri analitik lahir.

Pesawat Cartesian

Jika di pesawat dua garis tegak lurus dipilih yang berpotongan pada satu titik atau; dan jika juga setiap baris diberi arah dan skala numerik antara titik -titik yang berturut -turut, maka ada sistem atau rencana Cartesian di mana setiap titik pesawat dikaitkan dengan sepasang tertib dari dua bilangan real yang masing -masing proyeksi pada masing -masing pada tanggal tersebut sumbu x dan y.

Poin A = (3, 2); B = (-2, 3); C = (-2, -3) dan d = (3, -3) diwakili dalam bidang Cartesian seperti yang ditunjukkan di bawah ini:

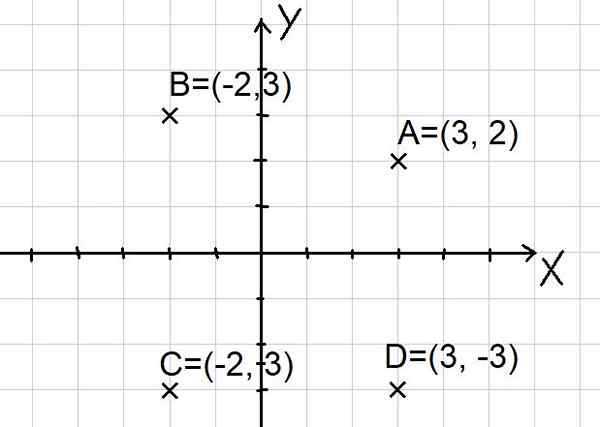Gambar 2. Poin di pesawat Cartesian. (Elaborasi sendiri)

Perhatikan bahwa dua sumbu X dan Y membagi bidang menjadi empat sektor yang disebut kuadran. Titik A ada di kuadran pertama, B di kuadran kedua, C di kuadran ketiga dan titik D di kuadran keempat.

Dapat melayani Anda: populasi dan sampel

Jarak antara dua titik

Jarak antara dua titik A dan B dari bidang Cartesian adalah panjang segmen yang menyatukan mereka. Jarak ini dapat dihitung secara analitis sebagai berikut:

D (a, b) = √ (bx - ax)^2 + (oleh - ay)^2)

Formula anterior diperoleh dengan menerapkan teorema Pythagoras.

Menerapkan formula tersebut ke poin A, B dari Gambar 2 adalah:

D (a, b) = √ (-2 - 3)^2 + (3 - 2)^2) = √ (-5)^2 + 1^2) = √ (26)

Yaitu, bahwa d (a, b) = 5.10 unit. Perhatikan bahwa jarak diperoleh tanpa perlu mengukur dengan aturan, prosedur aljabar yang sepenuhnya telah diikuti.

Ekspresi analitik dari suatu garis

Koordinat persegi panjang memungkinkan representasi analitik objek geometris mendasar seperti titik dan garis. Dua poin A dan B menentukan satu baris. Kemiringan garis didefinisikan sebagai hasil bagi antara perbedaan koordinat dan titik B lebih sedikit, dibagi dengan perbedaan koordinat x titik B kurang dari a:

tertunda = (oleh - ay)/(bx - ax)

Titik koordinat apa pun (x, y) yang termasuk dalam garis (AB) harus memiliki kemiringan yang sama:

tertunda = (y - ay)/(x - ax)

Persamaan yang diperoleh oleh kesetaraan lereng adalah representasi analitik atau aljabar dari garis yang melewati titik -titik A dan B:

(y - ay)/(x - ax) = (oleh - ay)/(bx - ax).

Jika Anda diambil untuk A dan B, koordinat persegi panjang dari Gambar 2 adalah:

(Y - 2)/(x - 3) = (3 - 2)/( - 2 - 3)

(y - 2)/(x - 3) = -⅕

Dalam kasus khusus ini ada garis dengan kemiringan negatif -⅕, yang berarti yang terletak di titik garis dan meningkatkan koordinat x dalam suatu unit, koordinat dan berkurang dalam 0,2 unit. 

Dapat melayani Anda: Toroid atau Toro Dona

Cara paling umum untuk menulis persamaan garis di pesawat adalah dengan koordinat dan jelas sebagai fungsi variabel x:

y = -(1/5) x + 13/5 

Contoh

Contoh 1

Diperoleh dengan metode analitik jarak antara titik c dan a, menjadi koordinat persegi panjang c = (-2, -3) dan yang dari a = (3.2).

Formula jarak Euclidean antara kedua titik ini ditulis seperti ini:

D (a, c) = √ ((cx - ax)^2 + (cy - ay)^2)

Mengganti koordinat persegi panjang yang sesuai yang Anda miliki:

D (a, c) = √ (-2-3)^2 + (-3-2)^2) = √ (-5)^2 + (-5)^2) = 5√2 = 7.07

Contoh 2

Dapatkan persamaan garis yang melewati titik C koordinat (-2, -3) dan titik p dari koordinat (2, 0).

Pertama, kemiringan garis CP diperoleh:

tertunda = (0 -(-3)) / (2 -( -2)) = ¾ 

Titik Q dari koordinat persegi panjang generik (x, y) milik garis CP harus memiliki kemiringan yang sama:

tertunda = (y -(-3)) / (x -( -2)) = (y +3) / (x +2)

Artinya persamaan garis CP adalah:

(Y +3) / (x +2) = ¾

Cara alternatif untuk menulis persamaan garis CP adalah kliring dan:

y = ¾ x - 3/2 

Latihan terpecahkan

Latihan 1

Dapatkan koordinat persegi panjang dari titik persimpangan antara garis y = - (1/5) x + 13/5 dan garis y = ¾ x - 3/2.

Solusi: Menurut definisi, titik persimpangan dari dua baris berbagi koordinat persegi panjang yang sama. Oleh karena itu, koordinat dan pada titik persimpangan identik untuk kedua baris:

-(1/5) x + 13/5 = ¾ x - 3/2

Apa yang mengarah pada ekspresi berikut:

Dapat melayani Anda: trapesium persegi panjang: sifat, hubungan dan formula, contoh

(¾ + ⅕) x = 13/5 +3/2

Memecahkan jumlah fraksi diperoleh:

19/20 x = 41/10

Kliring x:

x = 82/19 = 4.32

Untuk mendapatkan nilai dan persimpangan, nilai x yang diperoleh di salah satu baris diganti:

y = ¾ 4.32 - 3/2 = 1.74

Ini berarti bahwa garis yang diberikan dicegat pada titik I koordinat i = (4.32; 1,74).

Latihan 2

Dapatkan persamaan keliling yang melewati titik koordinat persegi panjang r (3, 4) dan yang memiliki pusat di asal koordinat.

Solusi: Radio R adalah jarak dari titik R ke asal atau koordinat (0, 0).

d (r, o) = √ ((rx - 0)^2 + (ry - 0)^2) = √ ((3 - 0)^2 + (4 - 0)^2) = √ (3^2 + 4^2) = √ (9 + 16) = √ (25) = 5

Artinya, ini adalah radius 5 lingkaran 5 yang berpusat pada (0,0).

Titik p (x, y) dari lingkar harus memiliki jarak 5 yang sama ke tengah (0, 0) untuk apa yang bisa ditulis:

D (p, o) = √ ((x - 0)^2 + (y - 0)^2) = √ (x^2 + y^2) = 5

Artinya:

√ (x^2 + y^2) = 5

Untuk menghilangkan akar kuadrat, kedua anggota kesetaraan dibiarkan diam -diam:

x^2 + y^2 = 25

Apa persamaan kelilingnya.

Dengan contoh ini kekuatan sistem koordinat persegi panjang diilustrasikan, yang memungkinkan untuk menentukan objek geometris, seperti keliling tanpa perlu menggunakan kertas, pensil dan kompas. Keliling yang diminta hanya dengan metode aljabar telah ditentukan.

Referensi

1. Arfken G dan Weber H. (2012). Metode Matematika untuk Fisikawan. Panduan komprehensif. Edisi ke -7. Pers Akademik. ISBN 978-0-12-384654-9
2. Perhitungan CC. Koordinat persegi panjang memecahkan masalah. Pulih dari: perhitungan.Dc
3. Weisstein, Eric W. “Koordinat Cartesian.”Dari MathWorld-A Wolfram Web. Dipulihkan dari: MathWorld.Wolfram.com
4. Wikipedia. Sistem koordinasi cartesian. Diperoleh dari: di.Wikipedia.com