Elemen Quadrilateral, Properti, Klasifikasi, Contoh

A berbentuk persegi Itu adalah poligon empat -sided dan empat simpul. Milik mereka sisi yang berlawanan Mereka adalah mereka yang tidak memiliki simpul yang sama, saat itu sisi berturut -turut Mereka yang memiliki titik umum.

Di segi empat sudut yang berdekatan Mereka yang berbagi sisi, sementara sudut yang berlawanan Mereka tidak memiliki sisi yang sama. Karakteristik penting lain dari segi empat adalah jumlah dari keempatnya Sudut internal Itu adalah dua kali sudut datar, yaitu 360º atau 2π RADIAN.

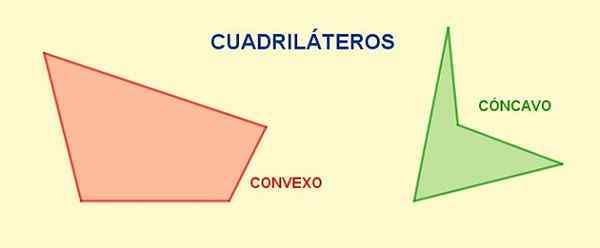
Gambar 1. Berbagai kuadrilateral. Sumber: f. Zapata.

Diagonal Mereka adalah segmen yang menyatukan simpul dengan kebalikannya dan di cincin yang diberikan, dari setiap simpul Anda dapat menggambar diagonal tunggal. Jumlah total diagonal dari segi empat adalah dua.

Quadrilateral adalah angka yang diketahui kemanusiaan sejak zaman kuno. Catatan arkeologis, serta konstruksi yang bertahan hari ini, membuktikannya.

Juga hari ini segi empat terus memiliki kehadiran penting dalam kehidupan sehari -hari semuanya. Pembaca dapat menemukan formulir ini di layar tempat teks dibaca pada saat yang tepat ini, di jendela, pintu, bagian otomotif dan banyak tempat lainnya.

[TOC]

Klasifikasi segi empat

Menurut paralelisme sisi yang berlawanan, segi empat diklasifikasikan sebagai berikut:

1. Trapesium, Saat tidak ada paralelisme dan segi empat adalah cembung.
2. Rekstok gantung, Saat ada paralelisme antara sepasang sisi yang berlawanan.
3. Genjang, Ketika sisi yang berlawanan mereka paralel dua banding.

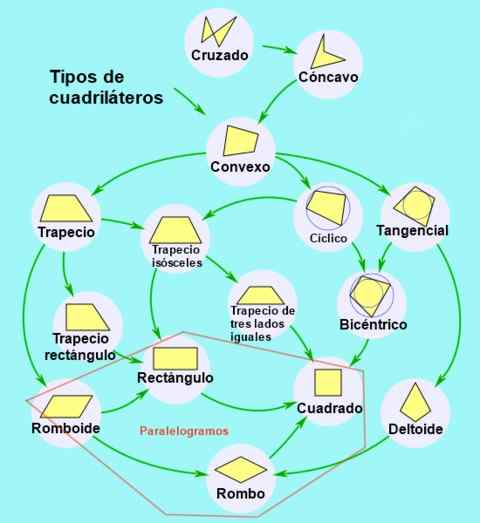Gambar 2. Klasifikasi dan subklasifikasi segi empat. Sumber: Wikimedia Commons.

Jenis jajaran genjang

Pada gilirannya, jajaran genjang dapat diklasifikasikan sesuai dengan sudut dan sisi mereka sebagai berikut:

1. Persegi panjang, Itu adalah jajaran genjang yang memiliki empat sudut internal dengan ukuran yang sama. Sudut internal persegi panjang membentuk sudut kanan (90º).
2. Persegi, Itu adalah persegi panjang dengan empat sisi dengan ukuran yang sama.
3. berlian, Itu adalah jajaran genjang dengan keempat sisinya, tetapi sudut yang berbeda yang berdekatan.
4. Genjang, jajaran genjang dengan sudut yang berdekatan yang berbeda.

Rekstok gantung

Trapeze adalah cembung segi empat dengan dua sisi paralel.

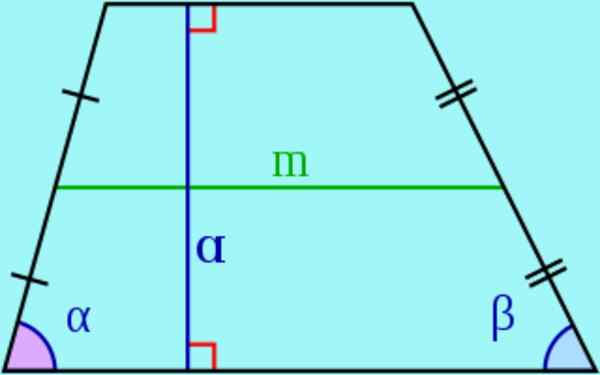Gambar 3. Pangkalan, lateral, tinggi dan median trapeze. Sumber: Wikimedia Commons.

- Dalam trapeze, sisi paralel disebut pangkalan Dan non -paralel disebut lateral.

- Itu tinggi dari trapeze adalah jarak antara dua pangkalan, yaitu, panjang segmen dengan ujung di pangkalan dan tegak lurus ke yang sama. Segmen ini juga disebut ketinggian trapeze.

- Itu median Itu adalah segmen yang bergabung dengan titik tengah sisi. Dapat ditunjukkan bahwa median sejajar dengan pangkalan trapeze dan panjangnya sama dengan semi -bodi pangkalan.

- Area trapeze adalah tinggi badannya dikalikan dengan semi -bodi pangkalan:

Area trapeze = tinggi * (basis 1 + basis 2) / 2

Jenis trapeze

-Trapeze persegi panjang: Ini adalah salah satu yang memiliki sisi tegak lurus terhadap pangkalan. Sisi ini juga ketinggian trapesium.

-Trapezium Isosceles: Yang dengan sisi panjang yang sama. Dalam trapesium Isosceles, sudut yang berdekatan dengan pangkalan adalah sama.

-Escaleno Trapezio: Orang yang memiliki sisi yang berbeda. Sudut yang berlawanan bisa akut dan tumpul lainnya, tetapi juga dapat terjadi bahwa keduanya tumpul atau keduanya akut.

Dapat melayani Anda: latihan faktorisasi terselesaikan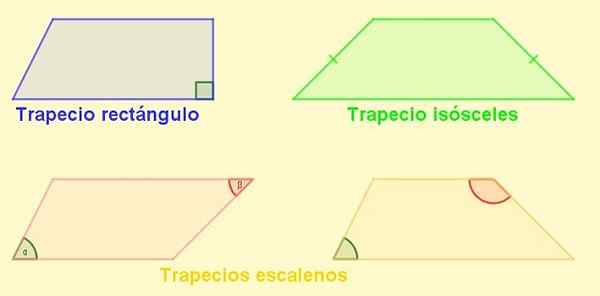 Gambar 4. Jenis trapeze. Sumber: f. Zapata.

Genjang

Guardelogram adalah segi empat yang sisi lawannya paralel dua banding. Dalam jajaran genjang, sudut yang berlawanan adalah sama dan sudut yang berdekatan bersifat tambahan, atau dengan kata lain, sudut yang berdekatan total 180º.

Jika jajaran genjang memiliki sudut yang tepat, maka semua sudut lainnya juga akan dan angka yang dihasilkan disebut persegi panjang. Tetapi jika persegi panjang juga memiliki sisi yang berdekatan dengan panjang yang sama, maka semua sisinya sama dan gambar yang dihasilkan adalah a persegi.

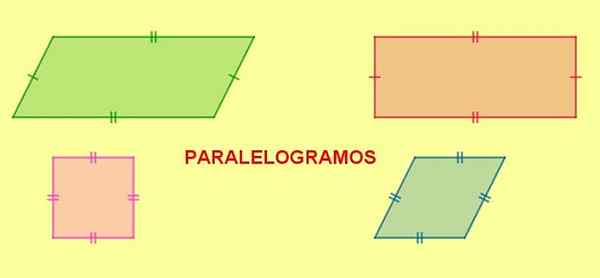Gambar 5. Jajaran genjang. Persegi panjang, persegi dan belah ketupat adalah jajaran genjang. Sumber: f. Zapata.

Ketika jajaran genjang memiliki dua sisi yang berdekatan dengan panjang yang sama, semua sisi akan memiliki panjang yang sama dan gambar yang dihasilkan adalah a berlian.

Ketinggian jajaran genjang adalah segmen dengan ujung pada sisi yang berlawanan dan tegak lurus bagi mereka.

Area jajaran genjang

Luas jajaran genjang adalah produk dari pangkalan dengan tinggi badannya, pangkalan menjadi sisi tegak lurus terhadap ketinggian (Gambar 6).

Area jajaran genjang = basis x tinggi = a . H

Diagonal sebuah jajaran genjang

Kuadrat diagonal yang dimulai dari titik sama dengan jumlah kotak dari kedua sisi yang berdekatan dengan simpul tersebut lebih banyak produk ganda dari sisi -sisi tersebut oleh cosinus sudut titik itu:

F² = a² +  D² + 2 a d cos (α)

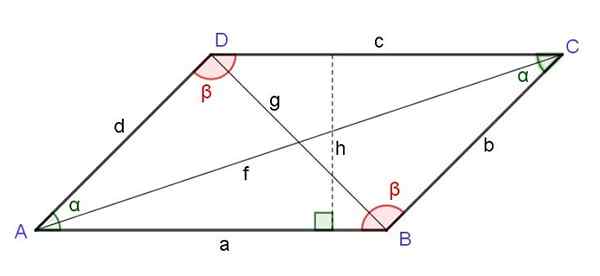Gambar 6. Genjang. Sudut yang berlawanan, tinggi, diagonal. Sumber: f. Zapata.

Kuadrat diagonal yang berlawanan dengan simpul jajaran genjang sama dengan jumlah kotak dari kedua sisi yang berdekatan dengan simpul tersebut dan mengurangi produk ganda dari sisi -sisi dengan cosinus dari sudut simpul itu:

G² = a² + D² - 2 a d cos (α)

Hukum jajaran genjang

Dalam jajaran genjang apa pun, jumlah kotak sisi mereka sama dengan jumlah kotak diagonal:

ke² + B² + C² + D² = f² + G²

Ulangctangle

Persegi panjang adalah segi empat dengan sisi yang berlawanan paralel dua banding dua dan yang juga memiliki sudut kanan. Artinya persegi panjang adalah jenis jajaran genjang dengan sudut kanan. Untuk menjadi jajaran genjang, Persegi panjang memiliki sisi berlawanan dengan panjang yang sama a = c dan b = d. 

Tetapi seperti pada sudut pandang jajaran genjang yang berdekatan adalah pelengkap dan sudut yang sama yang sama, dalam persegi panjang dengan memiliki sudut kanan, itu tentu akan membentuk sudut lurus di tiga sudut lainnya. Artinya Dalam persegi panjang semua sudut internal mengukur 90º atau π/2 radian.

Diagonal persegi panjang

Dalam persegi panjang diagonal panjangnya sama, Seperti yang akan ditunjukkan di bawah ini. Alasannya adalah sebagai berikut; Sebuah persegi panjang adalah jajaran genjang dengan semua sudut lurusnya dan itulah sebabnya ia mewarisi semua sifat jajaran genjang, termasuk rumus yang memberikan panjang diagonal:

F² = a²+  D² + 2 a d cos (α)

G² = a² + D² - 2 a d cos (α)

dengan α = 90º

Sebagai Cos (90º) = 0, Jadi itu terjadi itu:

F² = g² = a² +  D²

Itu adalah f = g, dan karena itu panjangnya F Dan G Dari dua diagonal persegi panjang mereka sama dan panjangnya diberikan oleh:

Panjang diagonal persegi panjang = √ (a² + B²)

Selain itu, jika dalam persegi panjang sisi yang berdekatan ke Dan B Satu sisi didasarkan pada sisi lain adalah tinggi dan akibatnya area persegi panjang adalah:

Ini dapat melayani Anda: Seri Fibonacci: Properti, Hubungan Alami, Aplikasi

Area persegi panjang = a x b.

Perimeter adalah jumlah dari semua sisi persegi panjang, tetapi karena lawannya sama, kemudian diperlukan untuk persegi panjang sisi ke Dan B Perimeter diberikan oleh formula berikut:

Perimeter persegi panjang = 2 (a + b)

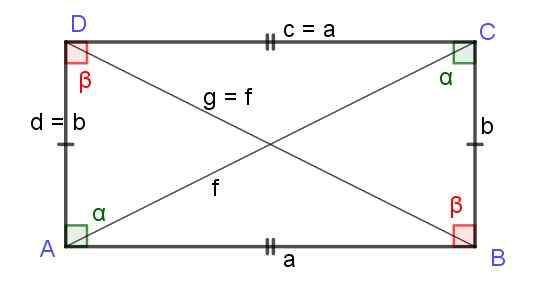Gambar 7. Persegi panjang sisi a dan b. Diagonal F dan G panjangnya sama. Sumber: f. Zapata.

Persegi

Kotak adalah persegi panjang dengan sisi yang berdekatan dengan panjang yang sama. Jika kotak memiliki sisi ke, Lalu diagonalnya F Dan G Mereka memiliki panjang yang sama, yaitu F = g = (√2) a.

Area persegi adalah sisi yang ditinggikan ke alun -alun:

Area persegi = a²

Perimeter persegi adalah dua kali sisi:

Perimeter persegi = 4 a

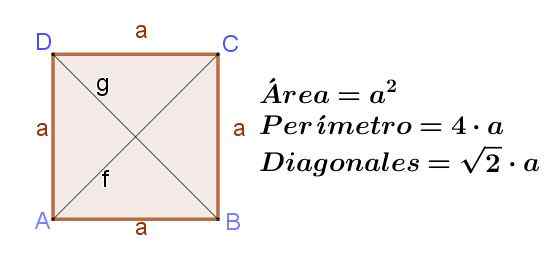Angka 8. Persegi ke sisi A, menunjukkan luasnya, perimeternya dan panjang diagonalnya. Sumber: f. Zapata ..

berlian

Belah ketupat adalah jajaran genjang dengan sisi yang berdekatan dengan panjang yang sama, tetapi seperti pada jajaran genjang, sisi yang berlawanan adalah sama, Semua sisi belah ketupat panjangnya sama.

Diagonal belah ketupat memiliki panjang yang berbeda, tetapi mereka dipotong pada sudut kanan.

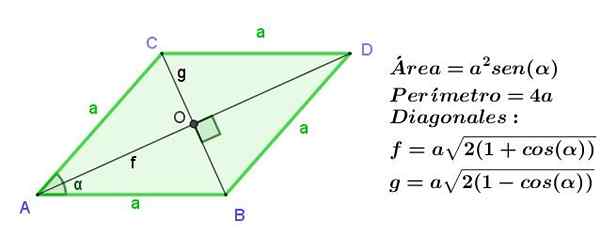Gambar 9. Belah ketupat dari sisi A, menunjukkan area, perimeter dan panjang diagonalnya. Sumber: f. Zapata.

Contoh

Contoh 1

Tunjukkan bahwa dalam segi empat (tidak disilangkan) sudut internal total 360º.

Gambar 10: Ini ditunjukkan sebagai jumlah sudut dari ADD quadrilateral 360º. Sumber: f. Zapata.

ABCD dianggap sebagai ABCD (lihat Gambar 10) dan BD diagonal ditarik. Dua segitiga ABD dan BCD terbentuk. Jumlah sudut internal segitiga ABD adalah:

α + β₁ + δ₁ = 180º

Dan jumlah sudut internal segitiga BCD adalah:

 β2 + γ + Δ₂ = 180º

Menambahkan dua persamaan diperoleh:

α + β₁ + δ₁ +  β₂ + γ + δ₂ = 180º + 180º

Pengelompokan:

α + (β₁ +  β₂) + (δ₁ + δ₂) + γ = 2* 180º

Mengelompokkan dan memperbarui, akhirnya ditunjukkan bahwa:

α + β + Δ + γ = 360º

Contoh 2

Tunjukkan bahwa median trapesium sejajar dengan pangkalannya dan panjangnya adalah semi -seismum dari pangkalan.

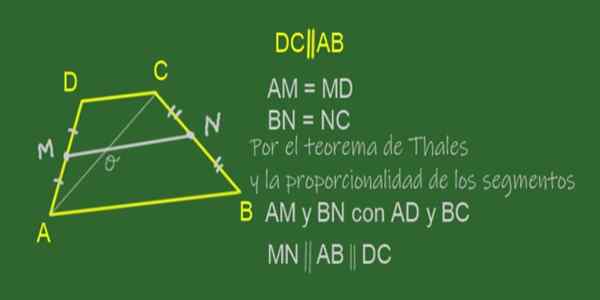Gambar 11. Median MN dari trapeze ABCD. Sumber: f. Zapata.

Median trapeze adalah segmen yang bergabung dengan titik tengah sisinya, yaitu, sisi non -paralel. Dalam trapeze ABCD yang ditunjukkan pada Gambar 11 mediannya adalah MN. 

Karena ini adalah titik tengah dari AD dan N Point BC Mid, dipenuhi bahwa quotients am / ad dan bn / bc sama.

Artinya, AM sebanding dengan BN dalam proporsi yang sama dengan AD adalah BC, sehingga kondisi untuk penerapan teorema (timbal balik) dari Thales yang menegaskan hal -hal berikut:

"Jika dalam tiga atau lebih lurus dipotong oleh dua secant".

Dalam kasus kami, disimpulkan bahwa garis MN, AB dan DC sejajar satu sama lain, oleh karena itu:

“LDi median salah satu trapeze sejajar dengan pangkalannya".

Dapat melayani Anda: Operasi gabungan

Sekarang Teorema Thales akan berlaku:

"Satu set paralel dipotong oleh dua atau lebih pengeringan menentukan segmen proporsional".

Dalam kasus kami AD = 2 pagi, AC = 2 AO, jadi segitiga DAC mirip dengan segitiga MAO, dan akibatnya DC = 2 bulan.

Argumen serupa memungkinkan untuk menegaskan bahwa Cu mirip dengan con, di mana ca = 2 co dan cb = 2 cn. Ini mengikuti ab = 2 on.

Singkatnya, ab = 2 pada y 2 mo. Jadi ketika kita telah pergi:

Ab + dc = 2 on + 2 mo = 2 (mo + on) = 2 mn

Akhirnya membersihkan MN:

Mn = (ab + dc) /2

Dan disimpulkan bahwa median trapesium mengukur semi -bodi pangkalan, atau dengan kata lain: median mengukur jumlah pangkalan, dibagi dengan dua.

Contoh 3

Menunjukkan bahwa dalam belah ketupat diagonal dipotong pada sudut kanan.

Gambar 12. Belah ketupat dan demonstrasi bahwa diagonal mereka dipotong pada sudut kanan. Sumber: f. Zapata.

Dewan Gambar 12 menunjukkan konstruksi yang diperlukan. Pertama, ABCD Guardelogram digambar dengan AB = BC, itu adalah belah ketupat. Diagonal AC dan DB menentukan delapan sudut yang ditunjukkan pada gambar.

Menggunakan teorema (a.yo.P.) yang menyatakan bahwa sudut alternatif internal antara paralel dipotong dengan penentuan sudut yang sama, kita dapat menetapkan yang berikut:

α₁ = γ₁, α2 = γ2, δ₁ = Β₁ dan Δ2 = β2. (*)

Di sisi lain, karena sisi yang berdekatan dari belah ketupat memiliki panjang yang sama, empat segitiga isosceles ditentukan:

DAB, BCD, CDA dan ABC

Sekarang Teorema Segitiga (Isosceles) dipanggil bahwa menyatakan bahwa sudut yang berdekatan dengan pangkalan memiliki ukuran yang sama, di mana disimpulkan bahwa:

δ₁ = β2, Δ2 = β₁, α2 = γ₁ dan α₁ = γ2 (**)

Jika hubungan (*) dan (**) digabungkan, kesetaraan sudut berikutnya tercapai:

α₁ = α2 = γ₁ = γ₁ Di satu sisi dan β₁ = Β2 = δ₁ = Δ2 untuk yang lain. 

Mengingat teorema segitiga yang sama yang menegaskan bahwa dua segitiga dengan sisi yang sama antara dua sudut yang sama adalah:

Aod = aob dan akibatnya juga sudut ∡aod = ∡aob.

Kemudian ∡AOD + ∡AOB = 180º, tetapi karena kedua sudutnya sama, 2 ∡AOD = 180º yang menyiratkan bahwa ∡AOD = 90º.

Yaitu, ditunjukkan secara geometris bahwa diagonal belah ketupat dipotong pada sudut kanan.

Latihan diselesaikan

- Latihan 1

Tunjukkan bahwa dalam trapesium persegi panjang, sudut non-EG adalah tambahan.

Larutan

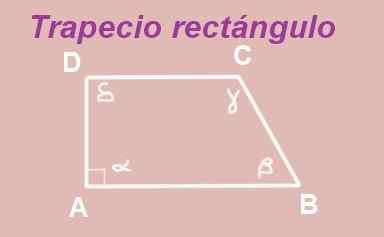Gambar 13. Trapeze persegi panjang. Sumber: f. Zapata.

ABCD Trapezoid dibangun dengan pangkalan AB dan DC paralel. Sudut bagian dalam vertex A lurus (mengukur 90º), jadi Anda memiliki trapesium persegi panjang.

Sudut α dan δ adalah sudut internal antara dua paralel paralel AB dan DC, oleh karena itu mereka sama, yaitu δ = α = 90º. 

Di sisi lain, telah ditunjukkan bahwa jumlah sudut internal segi empat menambahkan 360º, yaitu:

α + β + γ + δ = 90º + β + 90º + δ = 360º.

Hal di atas mengarah ke:

 β + Δ = 180º

Mengkonfirmasi apa yang ingin ditunjukkan bahwa sudut β dan Δ adalah tambahan.

- Latihan 2

ABCD Guardelogram memiliki AB = 2 cm dan AD = 1 cm, Selain itu sudutnya buruk adalah 30º. Tentukan area jajaran genjang tersebut dan panjang dua diagonalnya.

Larutan

Area jajaran genjang adalah produk dari panjang dasarnya dengan tinggi. Dalam hal ini, panjang segmen B = AB = 2 cm akan diambil sebagai alas, sisi lain memiliki panjang A = AD = 1 cm dan tinggi H akan dihitung sebagai berikut:

H = iklan * sin (30º) = 1 cm * (1/2) = ½ cm.

Kemudian: Area = B * H = 2 cm * ½ cm = 1 cm².

Referensi

1. C. DAN. KE. (2003). Elemen Geometri: Dengan Latihan dan Geometri Kompas. Universitas Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Grup Editorial Patria.
3. Freed, k. (2007). Temukan poligon. Perusahaan Pendidikan Benchmark.
4. Hendrik, v. (2013). Poligon umum. Birkhäuser.
5. Iger. (S.F.). Matematika semester pertama Tacaná. Iger.
6. Jr. Geometri. (2014). Poligon. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Matematika: Penalaran dan Aplikasi (Edisi Kesepuluh). Pendidikan Pearson.
8. Patiño, m. (2006). Matematika 5. Progreso editorial.
9. Wikipedia. Segi empat. Pulih dari: is.Wikipedia.com