Formula dan persamaan kuasivitas, contoh, olahraga

Itu penilaian semu, Varians kuasi atau varian yang tidak sehat adalah ukuran statistik dari dispersi data a Sampel Tentang rata -rata. Sampel pada gilirannya terdiri dari serangkaian data yang diambil dari alam semesta utama, yang disebut populasi.

Itu dilambangkan dalam beberapa hal, di sini telah dipilih S_C² Dan untuk menghitungnya, formula berikut mengikuti:

Gambar 1. Definisi kuasif. Sumber: f. Zapata.

Di mana:

-S_C ² = quatiriance atau varian sampel (varian sampel)

-X_yo = Masing -masing data sampel

-N = jumlah pengamatan

-X = Rata -rata sampel

Karena kesatuan quasivitas sampel adalah kuadrat dari unit di mana sampel datang, pada saat menafsirkan hasil yang lebih disukai untuk bekerja dengan Standar Deviasi Kuasi atau standar deviasi sampel.

Ini dilambangkan sebagai S_C Dan diperoleh dengan mengekstraksi akar kuadrat dari quasivariance:

S_C = √ s_C ²

Kuasirice mirip dengan varians S², dengan satu -satunya perbedaan yang ada dalam penyebutnya N-1, sementara dalam varian itu hanya dibagi oleh N. Jelas bahwa ketika n sangat besar, nilai -nilai keduanya cenderung sama.

Ketika nilai quatiriance diketahui, Anda dapat segera mengetahui bahwa varians.

[TOC]

Contoh kuasivitas

Anda ingin mengetahui karakteristik populasi apa pun: manusia, hewan, tumbuhan dan secara umum jenis objek apa pun. Tetapi menganalisis seluruh populasi mungkin bukan tugas yang mudah, terutama jika jumlah elemen sangat besar.

Kemudian sampel diambil, dengan harapan bahwa perilaku mereka mencerminkan bahwa dari populasi dan dengan demikian dapat membuat kesimpulan tentang hal itu, berkat sumber daya mana yang dioptimalkan. Ini dikenal sebagai Inferensi Statistik.

Berikut adalah beberapa contoh di mana kuasirice dan standar deviasi yang terkait dengan kuasi berfungsi sebagai indikator statistik dengan menunjukkan bahwa hasil yang diperoleh sehubungan dengan rata -rata.

Itu dapat melayani Anda: perimeter lingkaran: cara mengeluarkannya dan formula, latihan terpecahkan

1.- Direktur pemasaran perusahaan yang memproduksi baterai mobil perlu memperkirakan, dalam beberapa bulan, durasi baterai rata -rata.

Untuk melakukan ini, pilih secara acak sampel 100 baterai yang dibeli merek itu. Perusahaan menyimpan catatan data pembeli dan dapat mewawancarai mereka untuk mengetahui durasi baterai.

Gambar 2. Penilaian cuasive berguna untuk membuat kesimpulan dan kontrol kualitas. Sumber: Pixabay.

2.- Manajemen akademik lembaga universitas perlu memperkirakan pendaftaran tahun berikutnya, menganalisis jumlah siswa yang diharapkan untuk menyetujui mata pelajaran yang saat ini berada di.

Misalnya, dari masing -masing bagian yang saat ini mempelajari subjek fisik I, alamat tersebut dapat memilih sampel siswa dan menganalisis kinerjanya di kursi tersebut. Dengan cara ini Anda dapat menyimpulkan berapa banyak siswa yang akan belajar Fisika II di periode berikutnya.

3.- Sekelompok astronom memusatkan perhatian mereka pada bagian langit, di mana sejumlah bintang dengan karakteristik tertentu diamati: ukuran, massa dan suhu misalnya contoh.

Patut bertanya apakah bintang -bintang di wilayah serupa lainnya akan memiliki karakteristik yang sama, termasuk bintang di galaksi lain, seperti awan tetangga Magallanes atau Andromeda.

Mengapa Membagi Antara N-1?

Dalam quatirians dibagi antara N-1 alih-alih N Dan itu karena quatiriance adalah a Penaksir bersikeras, seperti yang dinyatakan di awal.

Kebetulan dari populasi yang sama dimungkinkan untuk mengekstrak banyak sampel. Varians dari masing -masing sampel ini juga dapat dirata -rata, tetapi rata -rata varian ini tidak menjadi sama dengan varian populasi.

Dapat melayani Anda: nilai relatif

Faktanya, rata -rata varian sampel cenderung meremehkan varian populasi, kecuali jika digunakan N-1 Di Denominator. Dapat diverifikasi bahwa nilai yang diharapkan dari kuasif E (s_C²) justru s².

Itulah sebabnya dikatakan bahwa quatiriance diinstal dan merupakan penduga yang lebih baik dari varians populasi².

Cara alternatif menghitung penilaian semu

Mudah ditunjukkan bahwa quatiriance juga dapat dihitung sebagai berikut:

S_C² = [∑x² / (N -1)] - [∑nx² / (N-1)]

Skor standar

Dengan memiliki penyimpangan dari sampel, kita dapat mengetahui berapa banyak standar deviasi yang memiliki nilai x tertentu, baik di atas atau di bawah rata -rata.

Untuk ini, ekspresi tanpa dimensi berikut digunakan:

Skor standar = (x - x) / s_C

Olahraga diselesaikan

Hitung quatiriance dan deviasi kuasi -tipikal dari data berikut, yang terdiri dari pembayaran bulanan dalam $ dilakukan oleh perusahaan asuransi ke klinik swasta.

863 903 957 1041 1138 1204 1354 1624 1698 1745 1802 1883

a) Gunakan definisi quasivitas yang diberikan di awal dan juga memverifikasi hasilnya dengan bentuk alternatif yang diberikan di bagian sebelumnya.

b) Hitung skor standar data kedua, membaca dari atas ke bawah.

Solusi untuk

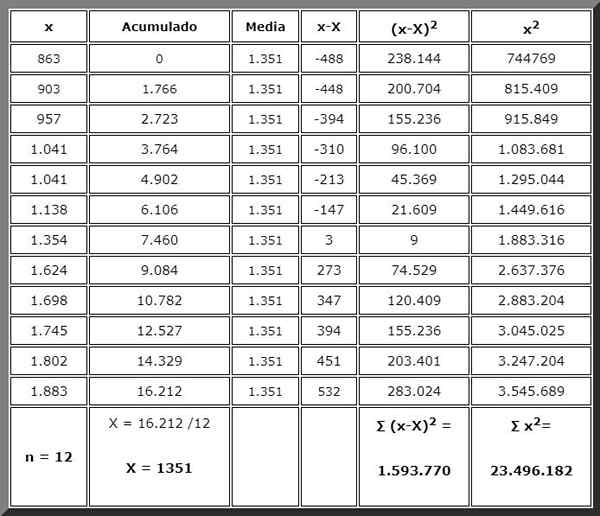
Masalahnya dapat diselesaikan dengan tangan dengan bantuan kalkulator sederhana atau ilmiah, yang harus kita lanjutkan secara berurutan. Dan untuk ini tidak ada yang lebih baik daripada mengatur data dalam tabel seperti yang ditunjukkan di bawah ini:

Berkat tabel Anda telah mengatur informasi dan jumlah yang akan diperlukan dalam rumus berada di akhir kolom masing -masing, siap digunakan segera. Summasi ditunjukkan dalam huruf tebal.

Dapat melayani Anda: apa 7 elemen keliling?

Kolom rata -rata selalu diulang, tetapi itu sepadan karena lebih mudah untuk memiliki nilai dalam tampilan, untuk mengisi setiap baris tabel.

Akhirnya, persamaan untuk quatiriance yang diberikan pada awalnya diterapkan, hanya nilai yang diganti dan dalam hal jumlah, kita sudah menghitungnya:

S_C² = 1.593.770 / (12-1) = 1.593.770 /11 = 144.888.2

Ini adalah nilai dari quasirians dan unit -unitnya adalah "dolar kuadrat", yang tidak masuk akal secara praktis, sehingga quasid standar sampel dihitung, yang tidak lebih dari akar kuadrat dari quasivariance:

S_C = (√144.888.2) $ = 380.64 $

Segera dikuatkan bahwa nilai ini juga diperoleh dengan bentuk alternatif dari quasivariance. Jumlah yang diperlukan adalah di akhir kolom terakhir di sebelah kiri:

S_C² = [∑x² / (N-) - [∑nx² / (N-1)] = [23.496.182/11] - [12 x 1351²/ sebelas]

= 2.136.016.55 - 1.991.128,36 = 144.$ 888 kuadrat

Itu adalah nilai yang sama yang diperoleh dengan formula yang diberikan di awal.

Solusi b

Nilai kedua dari atas ke bawah adalah 903, skor standarnya adalah

Skor standar 903 = (x - x) / s_C = (903 - 1351)/380.64 = -1.177

Referensi

1. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
4. Ukuran dispersi. Pulih dari: thales.Cica.adalah.
5. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.