Ukuran kecenderungan sentral untuk rumus data yang dikelompokkan, latihan

Itu Langkah -langkah tren pusat Mereka menunjukkan nilai di mana data distribusi berada. Yang paling terkenal adalah rata -rata rata -rata atau aritmatika, yang terdiri dari menambahkan semua nilai dan membagi hasilnya dengan jumlah total data.

Namun, jika distribusi terdiri dari sejumlah besar nilai dan tidak disajikan secara tertib, tidak mudah untuk melakukan perhitungan yang diperlukan untuk mengekstraksi informasi berharga yang dikandungnya.

Gambar 1. Langkah -langkah kecenderungan pusat untuk data yang dikelompokkan adalah indikatif yang baik dari perilaku data umum

Itulah sebabnya mereka dikelompokkan ke dalam kelas atau kategori, untuk menguraikan a distribusi Frekuensi. Melaksanakan urutan data sebelumnya ini, maka lebih mudah untuk menghitung langkah -langkah kecenderungan pusat, di antaranya adalah:

-Setengah

-Median

-Mode

-Rata -rata geometris

-Rata -rata harmonik

Rumus

Di bawah ini kami memiliki formula langkah -langkah kecenderungan pusat untuk data yang dikelompokkan:

Rata -rata aritmatika

Rata -rata adalah yang paling sering digunakan untuk mengkarakterisasi data kuantitatif (nilai numerik), meskipun cukup sensitif terhadap nilai distribusi ekstrem. Itu dihitung oleh:

Dengan:

-X: aritmatika rata -rata atau rata -rata

-F_yo: frekuensi kelas

-M_yo: Merek kelas

-G: Nomor kelas

-N: Total Data

Median

Untuk menghitungnya, perlu untuk menemukan interval yang berisi pengamatan n/2 dan interpolar untuk menentukan nilai numerik dari pengamatan tersebut, dengan cara rumus berikut:

Di mana:

-C: Lebar interval di mana median berada

-B_M: Perbatasan bawah interval tersebut

-F_M: Jumlah pengamatan yang terkandung dalam interval

-N/2: Total data dibagi dengan 2.

-F_Bm: Jumlah pengamatan sebelum interval yang mengandung median.

Oleh karena itu, median adalah ukuran posisi, yaitu, membagi data yang ditetapkan menjadi dua bagian. Mereka juga dapat didefinisikan kuartil, Desil Dan persentil, Itu membagi distribusi menjadi empat, sepuluh dan seratus bagian masing -masing.

Dapat melayani Anda: Fourier Transform: Properti, Aplikasi, Contoh

Mode

Dalam data yang dikelompokkan, kelas atau kategori yang berisi sebagian besar pengamatan dicari. Ini adalah Kelas Modal. Distribusi mungkin memiliki dua atau lebih mode, dalam hal ini disebut bimodal Dan Multimodal, masing -masing.

Anda juga dapat menghitung mode dalam data yang dikelompokkan mengikuti persamaan:

Dengan:

-L₁: Batas bawah kelas tempat mode berada

-Δ₁: Tetap antara frekuensi kelas modal dan frekuensi kelas yang mendahului itu.

-Δ₂: Kurangi antara frekuensi kelas modal dan frekuensi kelas yang mengikutinya.

-C: Lebar interval yang mengandung mode

Rata -rata harmonik

Rata -rata harmonik dilambangkan dengan h. Saat Anda memiliki satu set N Nilai x₁, X₂, X₃…, Rata -rata yang harmonis adalah terbalik atau timbal balik dari rata -rata aritmatika dari kebalikan dari nilai -nilai.

Lebih mudah melihatnya melalui formula:

Dan ketika memiliki data yang dikelompokkan, ekspresi diubah menjadi:

Di mana:

-H: Rata -rata harmonik

-F_yo: frekuensi kelas

-M_yo: Merek kelas

-G: Nomor kelas

-N = f₁ + F₂ + F₃ +..

Rata -rata geometris

kalau sudah N Bilangan positif x₁, X₂, X₃…, Rata-rata geometrisnya dihitung oleh N-EME dari produk dari semua angka:

Dalam kasus data yang dikelompokkan, dapat ditunjukkan bahwa logaritma desimal dari log rata -rata geometris, diberikan oleh:

Di mana:

-G: Rata -rata geometris

-F_yo: frekuensi kelas

-M_yo: Merek kelas

-G: Nomor kelas

-N = f₁ + F₂ + F₃ +..

Hubungan antara h, g dan x

Selalu benar bahwa:

H ≤ g ≤ x

Definisi yang paling digunakan

Definisi berikut diperlukan untuk menemukan nilai yang dijelaskan dalam rumus sebelumnya:

Frekuensi

Frekuensi didefinisikan sebagai berapa kali fakta diulangi.

Jangkauan

Itu adalah perbedaan antara nilai utama dan minor, hadir dalam distribusi.

Jumlah kelas

Untuk mengetahui berapa banyak kelas kami mengelompokkan data, kami menggunakan beberapa kriteria, misalnya yang berikut:

Dapat melayani Anda: 17 masalah yang beralasan

Batasan

Nilai ekstrem dari setiap kelas atau interval disebut batasan dan setiap kelas dapat memiliki kedua batas yang ditentukan dengan baik, dalam hal ini memiliki batas bawah dan satu lebih besar. Atau dapat memiliki batas terbuka, ketika rentang diberikan, misalnya nilai yang lebih besar atau lebih rendah dari angka tertentu.

Merek kelas

Ini hanya terdiri dari titik tengah interval dan dihitung rata -rata batas atas dan batas bawah.

Lebar interval

Data dapat dikelompokkan ke dalam kelas dengan ukuran yang sama atau berbeda, ini adalah lebar atau amplitudo. Pilihan pertama adalah yang paling banyak digunakan, karena memfasilitasi perhitungan, meskipun dalam beberapa kasus sangat penting bahwa kelas memiliki lebar yang berbeda.

Lebar C Dari interval itu dapat ditentukan dengan rumus berikut:

C = rentang / n_C

Di mana_C Itu adalah jumlah kelas.

Olahraga diselesaikan

Di bawah ini kami memiliki serangkaian pengukuran kecepatan dalam km/jam, diambil dengan radar, yang sesuai dengan 50 mobil yang melewati jalan di kota tertentu:

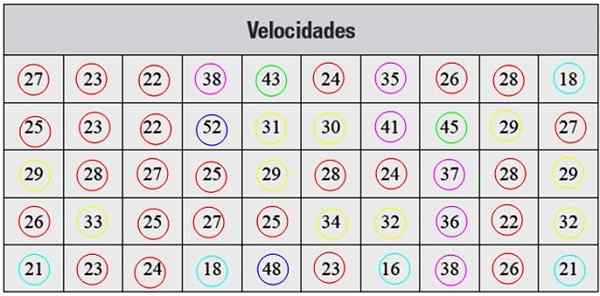Gambar 2. Tabel untuk latihan diselesaikan. Sumber: f. Zapata.

Larutan

Data yang disajikan tidak terorganisir, jadi langkah pertama adalah mengelompokkannya ke dalam kelas.

Langkah -langkah untuk mengelompokkan data dan membangun tabel

Langkah 1

Temukan rentang r:

R = (52 - 16) km/jam = 36 km/jam

Langkah 2

Pilih Jumlah Kelas N_C, Menurut kriteria yang diberikan. Karena ada 50 data, kami dapat memilih n_C = 6.

Langkah 3

Hitung lebarnya C dari interval:

C = rentang /n_C = 36/6 = 6

Langkah 4

Kelas bentuk dan data grup sebagai berikut: Untuk kelas pertama batas bawah dipilih segera setelah nilai yang lebih rendah dalam tabel ditambahkan ke nilai C = 6 ini, yang sebelumnya dihitung, dan dengan demikian memperoleh batas atas dari kelas utama.

Ini berjalan dengan cara yang sama untuk membangun sisa kelas, seperti yang ditunjukkan pada tabel berikut:

Dapat melayani Anda: apa itu nomor capicúa? Properti dan contoh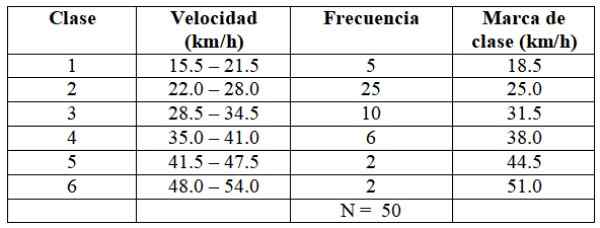

Setiap frekuensi sesuai dengan warna pada Gambar 2, dengan cara ini dipastikan bahwa tidak ada nilai keluar dari yang diperhitungkan.

Perhitungan rata -rata

X = (5 x 18.5 +25 x 25.0 + 10 x 31.5 + 6 x 38.0 + 2 x 44.5 + 2 x 51.0) ÷ 50 = 29.03 km/jam

Perhitungan median

Median ada di kelas 2 tabel, karena ada 30 data distribusi pertama.

-Lebar interval yang dimiliki median: C = 6

-Batas bawah interval di mana median berada: b_M = 22.0 km/jam

-Jumlah pengamatan yang terkandung dalam interval f_M = 25

-Total data dibagi dengan 2: 50/2 = 25

-Jumlah pengamatan sebelum interval yang mengandung median: f_Bm = 5

Dan operasinya adalah:

Median = 22.0 + [(25-5) ÷ 25] × 6 = 26.80 km/jam

Mode

Fashion juga ditemukan di Kelas 2:

-Lebar interval: C = 6

-Batas bawah kelas di mana fashion ditemukan: l₁ = 22.0

-Kurangi antara frekuensi kelas modal dan frekuensi kelas yang mendahului: Δ₁ = 25-5 = 20

-Kurangi antara frekuensi kelas modal dan frekuensi kelas yang mengikuti: Δ₂ = 25 - 10 = 15

Dengan data ini operasinya adalah:

Fashion = 22.0 + [20 ÷ (20 + 15)] x6 = 25.4 km/jam

Perhitungan rata -rata geometris

N = f₁ + F₂ + F₃ +... = 50

log g = (5 x log 18.5 + 25 x log 25 + 10 x log 31.5 + 6 x Log 38 + 2 × Log 44.5 + 2 x log 51) /50 =

log g = 1.44916053

G = 28.13 km/jam

Perhitungan rata -rata harmonik

1/jam = (1/50) x [(5/18.5) + (25/25) + (10/31.5) + (6/38) + (2/44.5) + (2/51)] = 0.0366

H = 27.32 km/jam

Ringkasan tindakan kecenderungan pusat

Unit variabel adalah km/jam:

-Media: 29.03

-Median: 26.80

-Fashion: 25.40

-Media Geometris: 28.13

-Rata -rata harmonik: 27.32

Referensi

1. Berenson, m. 1985. Statistik untuk Administrasi dan Ekonomi. Inter -American s.KE.
2. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
3. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
4. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
5. Spiegel, m. 2009. Statistik. Seri Schaum. 4 ta. Edisi. Bukit McGraw.
6. Pengobatan data yang dikelompokkan. Pulih dari: itchihuahua.Edu.MX.
7. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.