Apa rentang statistik? (Dengan contoh)

Dia jangkauan, Tur atau amplitudo, dalam statistik, adalah perbedaan (pengurangan) antara nilai maksimum dan nilai minimum satu set data dari sampel atau populasi. Jika kisaran dengan huruf R dan data diwakili dengan cara X, Formula untuk rentang itu sederhana:

R = x_Max - X_Min

 Dimana x_Max Itu adalah nilai maksimum data dan x_Min Ini adalah minimum.

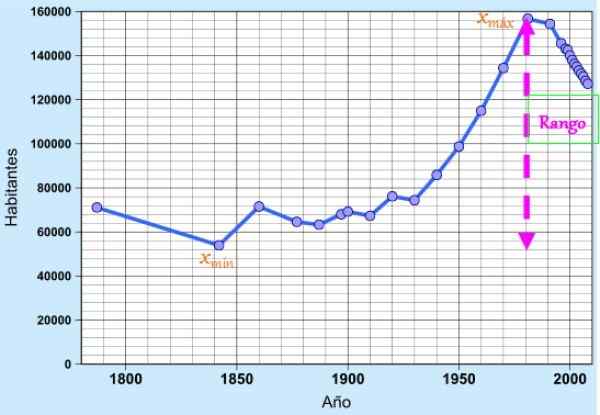
Gambar 1. Rentang data yang sesuai dengan populasi Cádiz dalam dua abad terakhir. Sumber: Wikimedia Commons.

Konsep ini sangat berguna sebagai ukuran dispersi sederhana untuk dengan cepat menghargai variabilitas data, karena menunjukkan ekstensi atau panjang interval di mana ini ditemukan.

Sebagai contoh, misalkan perawakan dari sekelompok 25 siswa laki -laki pada tahun pertama teknik di sebuah universitas. Siswa tertinggi dalam kelompok mengukur 1.93 m dan terendah 1.67 m. Ini adalah nilai ekstrem dari data sampel, oleh karena itu rute mereka adalah:

R = 1.93 - 1.67 m = 0.26 m atau 26 cm.

Perawakan siswa dari kelompok ini didistribusikan di seluruh kisaran ini.

[TOC]

Keuntungan dan kerugian

Kisarannya, seperti yang kami katakan sebelumnya, merupakan ukuran seberapa tersebar datanya. Kisaran kecil menunjukkan bahwa data kurang lebih dekat dan dispersi sedikit. Di sisi lain, kisaran yang lebih besar menunjukkan bahwa data lebih tersebar.

Keuntungan menghitung kisaran jelas: sangat sederhana dan cepat ditemukan, karena itu adalah perbedaan sederhana.

Ini juga memiliki unit yang sama dengan data yang bekerja dan konsepnya sangat mudah untuk ditafsirkan untuk pengamat mana pun.

Dalam contoh perawakan mahasiswa teknik, jika jangkauannya 5 cm, kami akan mengatakan bahwa siswa semuanya memiliki ukuran yang sama. Tetapi dengan kisaran 26 cm, kami segera berasumsi bahwa dalam sampel ada siswa dari semua statur menengah. Apakah asumsi ini selalu benar?

Itu dapat melayani Anda: perbedaan antara lingkaran dan keliling (dengan contoh)

Kekurangan kisaran sebagai ukuran dispersi

Jika kita melihat dengan cermat, dalam sampel 25 mahasiswa teknik, hanya satu dari mereka yang berukuran 1.93 dan 24 sisanya memiliki statur yang mendekati 1.67 m.

Namun kisarannya tetap sama, meskipun sangat mungkin terjadi bahwa kebalikannya terjadi: bahwa status mayoritas berosilasi sekitar 1.90 m dan hanya satu ukuran 1.67 m.

Bagaimanapun, distribusi data sangat berbeda.

Kerugian kisaran sebagai ukuran dispersi disebabkan oleh fakta bahwa ia hanya menggunakan nilai -nilai ekstrem dan mengabaikan semua yang lain. Karena sebagian besar informasi hilang, tidak ada tahu bagaimana data sampel didistribusikan.

Fitur penting lainnya adalah kisaran sampel tidak pernah berkurang. Jika kami menambahkan lebih banyak informasi, yaitu, kami mempertimbangkan lebih banyak data, rentangnya meningkat atau tetap sama.

Dan dalam hal apa pun, ini hanya berguna saat bekerja dengan sampel kecil, penggunaannya yang unik tidak direkomendasikan sebagai ukuran dispersi dalam sampel besar.

Apa yang perlu dilakukan adalah melengkapi dengan perhitungan langkah -langkah dispersi lain yang memperhitungkan informasi yang diberikan oleh total data: rute Interquartilic, Varians, standar deviasi dan koefisien variasi.

Rute interquirile, kuartil dan contoh terpecahkan

Kami telah menyadari bahwa kelemahan kisaran sebagai ukuran dispersi adalah bahwa ia hanya menggunakan nilai ekstrem dari distribusi data, menghilangkan yang lain.

Untuk menghindari ketidaknyamanan ini, kuartil: tiga nilai yang dikenal sebagai Langkah -langkah posisi.

Mereka mendistribusikan data yang tidak dikelompokkan ke dalam empat bagian (ukuran posisi lain yang banyak digunakan adalah Desil dan persentil). Ini adalah karakteristiknya:

-Q kuartil pertama₁ Itu adalah nilai data sehingga 25 % dari semuanya kurang dari q₁.

Dapat melayani Anda: Proporsionalitas Konstanta: Apa itu, Perhitungan, Latihan

-Q kuartil kedua₂ Ini adalah median distribusi, yang berarti bahwa setengah (50 %) dari data kurang dari nilai itu.

-Akhirnya q kuartil ketiga₃ menunjukkan bahwa 75 % dari data kurang dari q₃.

Kemudian, rentang interquotile atau rute interkuartil didefinisikan sebagai perbedaan antara q kuartil ketiga₃ dan q kuartil pertama₁ dari data:

Journey Intrisquotile = R_Q = Q₃ - Q₁

Dengan cara ini, nilai peringkat r_Q Itu tidak begitu terpengaruh oleh nilai -nilai ekstrem. Oleh karena itu disarankan untuk menggunakannya ketika datang ke distribusi yang bias, seperti siswa yang sangat tinggi atau sangat rendah yang dijelaskan di atas.

- Perhitungan Cuartyles

Ada beberapa cara untuk menghitungnya, di sini kami akan mengusulkan satu, tetapi dalam hal apa pun perlu untuk mengetahui jumlah pesanan "N_{salah satu}”, Yang merupakan tempat yang menempati kuartil masing -masing dalam distribusi.

Yaitu, jika misalnya istilah yang sesuai dengan q₁ adalah yang kedua, ketiga atau keempat dan sebagainya.

Kuartil pertama

N_{salah satu} (Q₁) = (N+1) / 4

Kuartil atau median kedua

N_{salah satu} (Q₂) = (N+1) / 2

Kuartil ketiga

N_{salah satu} (Q₃) = 3 (n+1) / 4

Dimana n adalah nomor data.

Median adalah nilai yang tepat di tengah distribusi. Jika nomor data ganjil tidak ada masalah dalam menemukannya, tetapi jika itu bahkan, maka dua nilai pusat dirata -rata untuk mengubahnya menjadi satu.

Setelah nomor pesanan dihitung, salah satu dari tiga aturan ini diikuti:

-Jika Anda tidak memiliki desimal, data yang ditunjukkan dalam distribusi dicari dan ini akan menjadi yang keempat dicari.

-Ketika nomor pesanan setengah jalan antara dua, maka data yang ditunjukkan oleh seluruh bagian dengan fakta berikut dirata -rata, dan hasilnya adalah kuartil yang sesuai.

-Dalam kasus lain, bilangan bulat terdekat dibulatkan dan itu akan menjadi tempat keempat.

Dapat melayani Anda: prinsip aditif

Contoh terpecahkan

Pada skala dari 0 hingga 20, sekelompok 16 siswa matematika saya memperoleh nilai (poin) berikut dalam ujian parsial:

16, 10, 12, 8, 9, 15, 18, 20, 9, 11, 1, 13, 17, 9, 10, 14

Menemukan:

a) rute data atau data.

b) Nilai kuartil q₁ dan q₃

c) rentang interquartil.

Gambar 2. Lakukan kualifikasi ujian matematika ini melakukan banyak variabilitas? Sumber: Pixabay.

Solusi untuk

Hal pertama yang harus dilakukan untuk menemukan rute adalah memesan data yang meningkat atau berkurang. Misalnya dalam meningkatkan urutan yang Anda miliki:

1, 8, 9, 9, 9, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18, 20

Melalui rumus yang diberikan di awal: r = x_Max - X_Min

R = 20 - 1 poin = 19 poin.

Menurut hasilnya, nilai -nilai ini memiliki dispersi yang bagus.

Solusi b

N = 16

N_{salah satu} (Q₁) = (N + 1) / 4 = (16 + 1) / 4 = 17/4 = 4.25

Itu adalah angka dengan desimal, yang seluruh bagiannya adalah 4. Kemudian kita pergi ke distribusi, data yang menempati tempat keempat dicari dan nilainya dirata -rata dengan posisi kelima. Karena keduanya 9, rata -rata juga 9 dan kemudian:

Q₁ = 9

Sekarang kami mengulangi prosedur untuk menemukan Q₃:

N_{salah satu} (Q₃) = 3 (n +1) / 4 = 3 (16 +1) / 4 = 12.75

Sekali lagi itu desimal, tetapi karena tidak setengahnya dibulatkan menjadi 13. Kuartil yang dicari menempati posisi tiga belas dan adalah:

Q₃ = 16

Solusi c

R_Q = Q₃ - Q₁ = 16 - 9 = 7 poin.

Yang seperti yang kita lihat jauh lebih sedikit dari rentang data yang dihitung di bagian A), karena peringkat minimum adalah 1 poin, nilai lebih jauh dari yang lain.

Referensi

1. Berenson, m. 1985. Statistik untuk Administrasi dan Ekonomi. Inter -American s.KE.
2. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
3. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
4. Contoh kuartil. Diperoleh dari: Mathematics10.bersih.
5. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.
6. Walpole, r. 2007. Probabilitas dan Statistik untuk Teknik dan Sains. Pearson.