U -test dari Mann - Whitney Apa dan ketika berlaku, eksekusi, contoh

Itu U -test of Mann - Whitney Ini diterapkan untuk membandingkan dua sampel independen ketika mereka memiliki sedikit data atau tidak mengikuti distribusi normal. Dengan cara ini, ini dianggap sebagai tes bukan parametrik, Tidak seperti rekan Anda Tes t Student, yang digunakan saat sampel cukup besar dan ikuti distribusi normal.

Frank Wilcoxon mengusulkannya untuk pertama kalinya pada tahun 1945, untuk sampel dengan ukuran yang identik, tetapi dua tahun kemudian diperpanjang dalam kasus sampel dengan ukuran berbeda oleh Henry Mann dan D. R. Whitney.

Gambar 1. Uji U -Mann - Whitney diterapkan untuk perbandingan sampel independen. Sumber: Pixabay.

Seringkali tes diterapkan untuk memverifikasi jika ada hubungan antara variabel kualitatif dan kuantitatif lainnya.

Contoh ilustrasi adalah mengambil satu set orang hipertensi dan mengekstrak dua kelompok, kepada siapa data tekanan darah harian dicatat selama sebulan.

Untuk satu kelompok perawatan A dan yang lain diterapkan pengobatan b. Di sini tekanan darah adalah variabel kuantitatif dan jenis pengobatannya adalah kualitatif.

Anda ingin tahu apakah median, dan bukan rata -rata, dari nilai yang diukur secara statistik sama atau berbeda, untuk menetapkan apakah ada perbedaan antara kedua perawatan. Untuk mendapatkan jawabannya, Wilcoxon atau U -test of Mann - Whitney diterapkan.

[TOC]

Pendekatan Masalah di U -Test of Mann - Whitney

Contoh lain di mana tes dapat diterapkan adalah sebagai berikut:

Misalkan Anda ingin tahu apakah konsumsi minuman ringan berbeda secara signifikan di dua daerah di negara ini.

Salah satunya disebut wilayah A dan wilayah lainnya b. Catatan liter yang dikonsumsi mingguan dalam dua sampel dilakukan: satu dari 10 orang untuk wilayah A dan satu lagi dari 5 orang untuk wilayah B.

Data adalah sebagai berikut:

-Wilayah a: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

-Wilayah b: 12,14, 11, 30, 10

Pertanyaan berikut diajukan:

Apakah konsumsi minuman ringan (Y) tergantung pada wilayah (x)?

Variabel kualitatif versus variabel kuantitatif

-Variabel kualitatif x: Wilayah

-Variabel kuantitatif dan: Konsumsi gas

Jika jumlah liter yang dikonsumsi adalah sama di kedua wilayah, kesimpulannya adalah bahwa tidak ada ketergantungan antara kedua variabel. Cara Mengetahui adalah dengan membandingkan tren rata -rata atau median untuk kedua daerah.

Kasus normal

Jika data mengikuti distribusi normal, dua hipotesis dinaikkan: null H0 dan alternatif H1 melalui perbandingan antara cara:

Dapat melayani Anda: produk terkenal

-H0: Tidak ada perbedaan antara rata -rata kedua daerah.

-H1: Sarana kedua daerah berbeda.

Kasing tanpa - kecenderungan normal

Sebaliknya, jika data tidak mengikuti distribusi normal atau hanya sampel sangat kecil untuk diketahui, alih -alih membandingkan rata -rata itu akan dibandingkan Mediannya dari dua wilayah.

-H0: Tidak ada perbedaan antara median dari dua daerah.

-H1: Median dari kedua daerah berbeda.

Jika median bertepatan, maka hipotesis nol terpenuhi: tidak ada hubungan antara konsumsi soda dan wilayah.

Dan jika sebaliknya terjadi, hipotesis alternatif adalah benar: ada hubungan antara konsumsi dan wilayah.

Ini untuk kasus -kasus di mana uji U Mann - Whitney diindikasikan.

Sampel atau sampel yang tidak diterjemas

Masalah penting berikut untuk memutuskan apakah uji U Mann Whitney diterapkan, adalah apakah jumlah data dalam kedua sampel identik, yang setara dengan mengatakan bahwa mereka pada saat yang sama.

Jika kedua sampel dipasangkan, versi Wilcoxon asli akan berlaku. Tetapi jika tidak, seperti halnya contohnya, maka uji Wilcoxon yang dimodifikasi diterapkan, yang justru uji U Mann Whitney.

Mann Whitney U Tes karakteristik

Uji u -u -Whitney Tes non -parametrik, berlaku untuk sampel yang tidak mengikuti distribusi normal atau dengan sedikit data. Ini memiliki karakteristik berikut:

1.- Bandingkan mediannya

2.- Bekerja pada rentang yang dipesan

3.- Ini kurang kuat, pemahaman dengan kekuatan probabilitas menolak hipotesis nol ketika pada kenyataannya itu salah.

Dengan mempertimbangkan karakteristik ini, uji -U Mann - Whitney diterapkan saat:

-Datanya independen

-Mereka tidak mengikuti distribusi normal

-Hipotesis NULL H0 diterima jika media dari dua sampel bertepatan: MA = MB

-Hipotesis alternatif H1 diterima jika media dari dua sampel berbeda: ma ≠ mb

Formula Mann - Whitney

Variabel U adalah statitas kontras yang digunakan dalam uji Mann - Whitney dan didefinisikan:

U = min (ua, ub)

Ini berarti bahwa U adalah nilai paling sedikit antara UA dan UB, diterapkan untuk masing -masing kelompok. Dalam contoh kami itu akan ke setiap wilayah: A o b.

Variabel UA dan UB didefinisikan dan dihitung sesuai dengan rumus berikut:

Ua = nb + na (na +1)/2 - ra

UB = NB + NB (NB +1)/2 - RB

Dapat melayani Anda: pengurangan istilah serupa

Di sini nilai Na dan NB adalah ukuran sampel yang sesuai dengan daerah A dan B masing -masing dan di sisi lain, RA dan RB adalah yang Jumlah rentang bahwa kami akan mendefinisikan di bawah ini.

Langkah -langkah untuk menerapkan tes

1.- Pesan nilai dari kedua sampel.

2.- Tetapkan rentang pesanan untuk setiap nilai.

3.- LIGATUR YANG TERBUKA DALAM DATA (Nilai berulang).

4.- Hitung RA = jumlah rentang sampel a.

5.- Temukan RB = jumlah rentang sampel b.

6.- Tentukan nilai UA dan UB, sesuai dengan rumus yang diberikan di bagian sebelumnya.

7.- Bandingkan UA dan UB, dan minor dari keduanya ditugaskan untuk statistik atau eksperimental (yaitu data) dibandingkan dengan statistik teoretis atau normal.

Aplikasi Praktis Aplikasi

Sekarang kami menerapkan yang disebutkan di atas untuk masalah soda yang sebelumnya diangkat:

Wilayah A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12

Wilayah B: 12,14, 11, 30, 10

Bergantung bahwa sarana kedua sampel secara statistik sama atau berbeda, kami melanjutkan untuk menerima atau menolak hipotesis nol: tidak ada hubungan antara variabel dan dan x, yaitu, konsumsi soda tidak bergantung pada wilayah tersebut:

H0: ma = mb

H1: ma ≠ mb

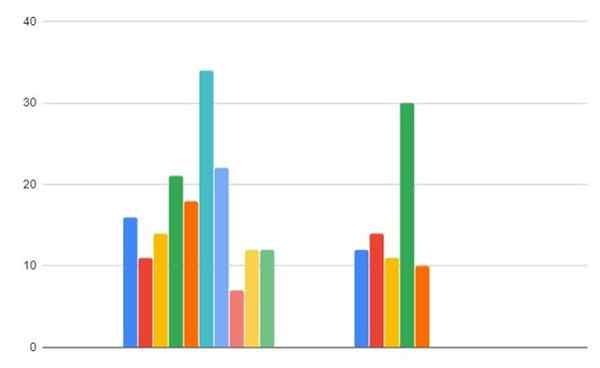Gambar 2. Data konsumsi gas di wilayah A dan B. Sumber: f. Zapata.

- Langkah 1

Kami melanjutkan untuk memesan data bersama untuk dua sampel, memesan nilai dari paling sedikit ke yang terbesar:

Perhatikan bahwa nilai 11 muncul 2 kali (sekali dalam setiap sampel). Awalnya ia memiliki posisi atau rentang 3 dan 4, tetapi tidak terlalu tinggi atau meremehkan satu atau yang lain nilai rata -rata dipilih sebagai kisaran, yaitu 3,5.

Demikian pula, nilai 12 dilanjutkan, yang diulang tiga kali dengan rentang 5, 6 dan 7.

Nah, nilai 12 ditetapkan kisaran rata -rata 6 = (5+6+7)/3. Dan sama untuk nilai 14, yang memiliki ligasi (muncul di kedua sampel) di posisi 8 dan 9, kisaran rata -rata 8 ditetapkan.5 = (8+9)/2.

- Langkah 2

Data untuk wilayah A dan B kemudian dipisahkan lagi tetapi sekarang rentang yang sesuai ditetapkan di baris lain:

Wilayah a

Wilayah b

Rentang RB diperoleh dari jumlah elemen baris kedua untuk setiap kasus atau wilayah.

Langkah 3

Nilai masing -masing UA dan UB dihitung:

Ua = 10 × 5 + 10 (10 + 1)/2 - 86 = 19

UB = 10 × 5 + 5 (5 + 1)/2 -34 = 31

Nilai eksperimental u = min (19, 31) = 19

Langkah 4

Ahli teori seharusnya mengikuti distribusi normal n dengan parameter yang diberikan secara eksklusif dengan ukuran sampel:

Dapat melayani Anda: bilangan irasional: sejarah, sifat, klasifikasi, contoh

N ((na⋅nb) /2, √ [nb (na + nb +1) /12])

Untuk membandingkan variabel atau diperoleh secara eksperimental, dengan teoritis, perlu membuat perubahan variabel. Itu beralih dari variabel atau eksperimental ke nilainya ditiru, yang akan disebut Z, Agar dapat membandingkan dengan distribusi normal yang ditandai.

Perubahan variabel adalah sebagai berikut:

Z = (u - na.Nb / 2) / √ [na. NB (Na + NB + 1) / 12] 

Perlu dicatat bahwa untuk perubahan variabel parameter distribusi teoritis untuk U digunakan. Maka variabel z baru, yang merupakan hibrida antara teoritis dan distribusi eksperimental atau normal yang ditiru n (0,1).

Kriteria perbandingan

Jika z ≤ zα ⇒ Hipotesis NULL H0 diterima

Ya z> zα ⇒ Hipotesis NULL H0 ditolak

Nilai kritis Zα yang ditandai tergantung pada tingkat kepercayaan yang diperlukan, misalnya untuk tingkat kepercayaan α = 0,95 = 95% yang paling umum memiliki nilai kritis Zα = 1,96.

Untuk data yang ditampilkan di sini:

Z = (u - nb / 2) / √ [nb (na + nb + 1) / 12] = -0.73

Yang di bawah nilai kritis 1.96.

Maka kesimpulan terakhir adalah bahwa hipotesis nol diterima:

Tidak ada perbedaan dalam konsumsi soda antar daerah A dan B.

Kalkulator Online untuk U -Test of Mann - Whitney

Ada program khusus untuk perhitungan statistik, termasuk SPSS dan Minitab, tetapi program ini dibayar dan penggunaannya tidak selalu sederhana. Ini karena mereka memberikan begitu banyak opsi, bahwa penggunaannya secara praktis disediakan untuk para ahli statistik.

Untungnya, ada beberapa program online yang sangat tepat, gratis dan sederhana yang memungkinkan antara lain untuk tes U -whitney U.

Program -program ini adalah:

-Statistik Ilmu Sosial (Socscistatistics.com), yang memiliki uji U-Whitney U dan Wilcoxon dalam kasus sampel seimbang atau berpasangan.

-Statistik terapi AI (AI-terapi.com), yang memiliki beberapa tes statistik deskriptif biasa.

-Statistik untuk digunakan (fisika.CSBSJU.Edu/statistik), salah satu yang tertua, sehingga antarmuka Anda dapat terlihat sudah usang, meskipun ini adalah program gratis yang sangat efisien.

Referensi

1. Dietrichson. Metode Kuantitatif: Tes Rentang. Pulih dari: bookdown.org
2. Marín J p. Panduan SPSS: Analisis dan Prosedur dalam Tes Non -Parametrik. Pulih dari: halweb.UC3M.adalah
3. USAL MOOC. Tes non -parametrik: U of Mann - Whitney. Dipulihkan dari: YouTube.com
4. Wikipedia. U -test of Mann - Whitney. Pulih dari: is.Wikipedia.com
5. Xlstat. Pusat Bantuan. Tutorial Tes Mann - Whitney di Excel. Pulih dari: bantuan.Xlsat.com