Derajat kebebasan bagaimana menghitungnya, jenis, contoh

Itu derajat kebebasan Dalam statistik adalah jumlah komponen independen dari vektor acak. Jika vektor memiliki N komponen dan ada P persamaan linier yang menghubungkan komponennya, lalu tingkat kebebasan Itu n-p.

Konsep derajat kebebasan Ini juga muncul dalam mekanika teoritis, di mana dalam mode kotor mereka setara dengan dimensi ruang di mana partikel bergerak, kecuali jumlah ligatur.

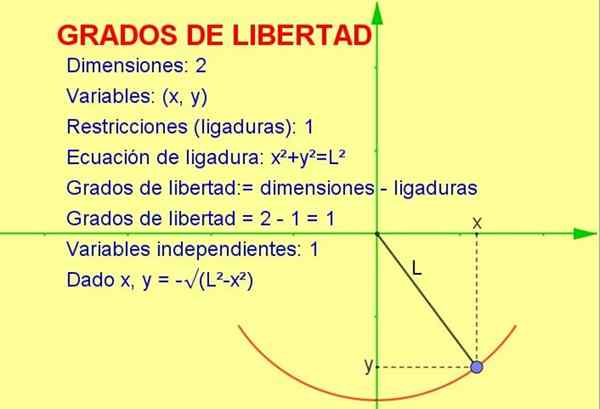
Gambar 1. Pendulum bergerak dalam dua dimensi, tetapi hanya memiliki tingkat kebebasan karena diwajibkan untuk bergerak dalam radius busur l. Sumber: f. Zapata.

Artikel ini akan membahas konsep derajat kebebasan yang diterapkan pada statistik, tetapi contoh mekanis lebih mudah divisualisasikan dengan cara geometris.

[TOC]

Jenis derajat kebebasan

Menurut konteks di mana ia diterapkan, cara menghitung jumlah derajat kebebasan dapat bervariasi, tetapi ide yang mendasarinya selalu sama: dimensi total lebih sedikit jumlah pembatasan.

Dalam kasus mekanis

Pertimbangkan partikel yang berosilasi yang diikat ke tali (pendulum) yang bergerak dalam bidang vertikal X-Y (2 dimensi). Namun, partikel tersebut berkewajiban untuk bergerak pada lingkar jari -jari yang sama dengan panjang tali.

Karena partikel hanya dapat bergerak pada kurva itu, jumlahnya derajat kebebasan Itu 1. Ini dapat divisualisasikan dalam Gambar 1.

Cara untuk menghitung jumlah derajat kebebasan adalah dengan membuat perbedaan dalam jumlah dimensi kecuali jumlah pembatasan:

Derajat kebebasan: = 2 (dimensi) - 1 (ligasi) = 1

Penjelasan lain yang memungkinkan kita mencapai hasilnya adalah sebagai berikut:

-Kita tahu bahwa posisi dua dimensi diwakili oleh titik koordinat (x, y).

-Tetapi karena intinya harus memenuhi persamaan keliling (x² + Dan² = L²) Untuk nilai variabel x yang diberikan, variabel dan ditentukan oleh persamaan atau pembatasan tersebut.

Dengan cara ini, hanya satu dari variabel yang independen dan sistem memiliki Satu (1) tingkat kebebasan.

Dapat melayani Anda: probabilitas klasik: perhitungan, contoh, latihan terpecahkan

Dalam satu set nilai acak

Untuk mengilustrasikan apa arti konsep tersebut, anggaplah vektor

X = (x₁, X₂,…, X_N)

Mewakili sampel N Nilai acak didistribusikan secara normal. Dalam hal ini vektor acak X memiliki N komponen independen dan karena itu dikatakan itu X memiliki n derajat kebebasan.

Mari Bangun Vektor Sekarang R dari limbah

R = (x₁ - , X₂ - ,.. ., X_N - )

Di mana itu mewakili rata -rata sampel, yang dihitung sebagai berikut:

= (x₁ + X₂ +.. .+ X_N) / N

Lalu jumlahnya

(X₁ - )+(x₂ - )+.. .+(X_N - ) = (x₁ + X₂ +.. .+ X_N) - n = 0

Ini adalah persamaan yang mewakili pembatasan (atau ligasi) dalam elemen vektor R dari limbah, karena jika N-1 diketahui, komponen vektor R, Persamaan pembatasan menentukan komponen yang tidak diketahui.

Oleh karena itu vektor R dimensi n dengan pembatasan:

∑ (x_yo - ) = 0

Memiliki (N - 1) derajat kebebasan.

Sekali lagi diterapkan bahwa perhitungan jumlah derajat kebebasan adalah:

derajat kebebasan: = n (dimensi) - 1 (pembatasan) = n -1

Contoh

Varians dan derajat kebebasan

Varians s² Ini didefinisikan sebagai rata -rata kuadrat penyimpangan (atau limbah) sampel data:

S² = (R•R) / (N-1)

Di mana R adalah vektor limbah R = (x1 -, x2 -, .. ., Xn -) dan titik tebal (•) adalah operator produk skalar. Atau, rumus varians dapat ditulis sebagai berikut:

S² = ∑ (x_yo - )² / (N-1)

Dalam kasus apa pun, perlu dicatat bahwa ketika menghitung rata-rata kuadrat limbah, itu dibagi dengan (n-1) dan bukan antara N, karena seperti yang dibahas pada bagian sebelumnya, jumlah derajat kebebasan dari vektor R adalah (n-1).

Jika untuk perhitungan varians itu dibagi antara N Alih-alih (N-1), hasilnya akan memiliki bias yang sangat signifikan untuk nilai-nilai N kurang dari 50.

Itu dapat melayani Anda: geometri analitik

Dalam literatur juga muncul rumus varian dengan pembagi n alih-alih (n-1), ketika datang ke varian populasi.

Tetapi himpunan variabel acak limbah, diwakili oleh vektor R, Meskipun memiliki dimensi n, ia hanya memiliki (N-1) derajat kebebasan. Namun, jika nomor data cukup besar (n> 500), kedua rumus itu menyatu dengan hasil yang sama.

Kalkulator dan spreadsheet menawarkan dua versi varian dan standar deviasi (yang merupakan akar kuadrat dari varian).

Rekomendasi kami, mengingat analisis yang disajikan di sini, adalah untuk selalu memilih versi dengan (N-1) setiap kali diperlukan untuk menghitung varians atau standar deviasi, untuk menghindari hasil dengan bias.

Dalam distribusi chi square

Beberapa distribusi probabilitas dalam variabel acak kontinu tergantung pada parameter yang disebut tingkat kebebasan, Ini adalah kasus distribusi chi square (χ²).

Nama parameter tersebut berasal dari tingkat kebebasan vektor acak yang mendasari distribusi ini diterapkan.

Asumsikan bahwa ada populasi G, di mana sampel ukuran N diambil:

X₁ = (x1₁, x1₂,... x1_N)

X2 = (x2₁, x2₂,... x2_N)

.. .

X_J = (xj₁, xj₂,… XJ_N)

.. .

Xg = (xg₁, Xg₂,… Xg_N)

Suatu populasi J yang memiliki rata -rata dan standar deviasi SJ, Ikuti distribusi normal n (, SJ ).

ZJ variabel yang ditiru atau dinormalisasi_yo didefinisikan sebagai:

ZJ_yo = (xj_yo - ) / SJ.

Dan vektor ZJ Itu didefinisikan seperti ini:

ZJ = (Zj₁, ZJ₂,…, ZJ_yo,…, ZJ_N) Dan ikuti distribusi normal yang ditiru n (0,1).

Lalu variabelnya:

Q = ((Z1₁ ^2 + z2₁^2+… . + Zg₁^2),… ., (Z1_N^2 + z2_N^2+… . + Zg_N^2))

Ikuti distribusi χ²(g) disebut Distribusi chi square dengan tingkat kebebasan G.

Dalam kontras hipotesis (dengan contoh terselesaikan)

Ketika Anda ingin membuat kontras hipotesis berdasarkan pada set data acak tertentu, perlu untuk mengetahui Jumlah derajat kebebasan g Untuk dapat menerapkan tes chi square.

Dapat melayani Anda: distribusi seragam kontinu: karakteristik, contoh, aplikasi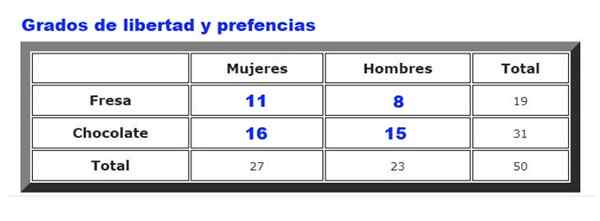 Gambar 2. Apakah ada hubungan antara rasa es krim dan jenis kelamin pelanggan? Sumber: f. Zapata.

Sebagai contoh, data yang dikumpulkan pada cokelat atau preferensi es krim stroberi antara pria dan wanita di beberapa toko es krim akan dianalisis. Frekuensi pria dan wanita memilih stroberi atau cokelat, dirangkum dalam Gambar 2.

Pertama, tabel frekuensi yang diharapkan dihitung, yang dibuat dengan mengalikan Total baris untuk dia Total kolom, dibagi dengan Total data. Hasilnya ditunjukkan pada gambar berikut:

Gambar 3. Perhitungan frekuensi yang diharapkan berdasarkan frekuensi yang diamati (nilai biru pada Gambar 2). Sumber: f. Zapata.

Kemudian kami melanjutkan untuk menghitung kuadrat CHI (dari data) dengan formula berikut:

χ² = ∑ (f_{salah satu} - F_Dan)² / F_Dan

Dimana f_{salah satu} adalah frekuensi yang diamati (Gambar 2) dan f_Dan adalah frekuensi yang diharapkan (Gambar 3). Jumlahnya lebih dari semua peringkat dan kolom, yang dalam contoh kami memberikan empat istilah.

Setelah melakukan operasi yang Anda dapatkan:

χ² = 0,2043.

Sekarang perlu dibandingkan dengan kuadrat teoretis, yang tergantung pada Jumlah derajat kebebasan g.

Dalam kasus kami, nomor ini ditentukan sebagai berikut:

G = (#filas - 1) (#Columnas - 1) = (2 - 1) (2 - 1) = 1 * 1 = 1.

Ternyata jumlah derajat kebebasan g dari contoh ini adalah 1.

Jika Anda ingin memverifikasi atau menolak hipotesis nol (H0: tidak ada korelasi antara rasa dan jenis kelamin) dengan tingkat signifikansi 1%, kuadrat CHI teoritis dihitung dengan tingkat kebebasan g = 1.

Nilai yang membuat frekuensi akumulasi dicari (1 - 0.01) = 0.99, itu 99%. Nilai ini (yang dapat diperoleh dari tabel) adalah 6.636.

Saat chi teoretis melampaui yang dihitung, maka hipotesis nol diverifikasi.

Yaitu, dengan data yang dikumpulkan, tidak ada hubungan antara rasa variabel dan jenis kelamin.

Referensi

1. Minitab. Berapa derajat kebebasan? Diperoleh dari: Dukungan.Minitab.com.
2. Moore, David. (2009) Statistik Terapan Dasar. Editor Antoni Bosch.
3. Leigh, Jennifer. Bagaimana Menghitung Tingkat Kebebasan dalam Model Statistik. Pulih dari: geniolandia.com
4. Wikipedia. Tingkat Kebebasan (Statistik). Pulih dari: is.Wikipedia.com
5. Wikipedia. Tingkat Kebebasan (Fisik). Pulih dari: is.Wikipedia.com