Turunan implisit bagaimana mereka diselesaikan dan diselesaikan latihan

Itu turunan implisit Mereka adalah alat yang digunakan dalam teknik diferensiasi yang diterapkan pada fungsi. Mereka berlaku ketika tidak mungkin, di bawah metode reguler, melakukan pembersihan variabel dependen yang diturunkan. Izin ini dilakukan berdasarkan variabel independen.

Misalnya, dalam ekspresi 3xy³ - 2y + xy² = xy, Anda tidak bisa mendapatkan ekspresi yang mendefinisikan "y" tergantung pada "x". Sehingga ketika ekspresi diferensial DY/DX dapat diperoleh.

[TOC]

Bagaimana turunan implisit diselesaikan?

Untuk memecahkan implikasi, itu didasarkan pada ekspresi implisit. Misalnya: 3xy³ - 2y + xy² - Xy = 0. Ini telah jelas dibersihkan, namun untuk melakukannya bukanlah kondisi yang diperlukan untuk mendapatkan turunan dari y mengenai x. Kemudian, masing -masing elemen diturunkan menghormati aturan rantai untuk fungsi campuran:

3xy³ Ini terdiri dari 2 variabel, oleh karena itu d (3xy³) Ini akan diperlakukan sebagai turunan dari produk fungsi.

D (3xy³)/dx = 3y³ + 3y².(3x) dan '= 3y³ + 9xy² Dan'

Di mana elemen dan 'dikenal sebagai "dan sepupu”Dan DY/DX mewakili

-2y berasal sesuai dengan hukum k.U = k.ATAU'

D (-2y) = -2 dan '

Xy² misalkan diferensial lain yang terdiri dari produk fungsi

D (xy²) = y² + 2xy dan '

-XY adalah cara yang homolog

d (-xy) = -y -x dan '

Mereka diganti dalam kesetaraan, mengetahui bahwa turunan nol adalah nol.

3y³ + 9xy² dan ' - 2 dan' + dan² + 2xy dan ' - y - x dan' = 0

Elemen -elemen yang memiliki istilah dan 'dikelompokkan bersama di satu sisi kesetaraan

Dapat melayani Anda: vektor kolineal

3y³ + Dan² - y = -9xy² dan ' + 2 dan' + x dan '

Faktor umum dan 'anggota yang tepat dari kesetaraan diekstraksi

3y³ + Dan² - y = y '(-9xy² + x + 2)

Akhirnya, istilah yang berlipat ganda dan '. Dengan demikian mendapatkan ekspresi yang sesuai dengan turunan implisit y mengenai x.

dan '= dy/dx = (3y³ + Dan² - y)/(-9xy² + x + 2)

Aturan rantai

Dalam derivasi implisit aturan rantai selalu dihormati. Semua ekspresi diferensial akan diberikan tergantung pada variabel independen x. Sehingga variabel apa pun θ berbeda dari x harus mencakup istilah dθ/dx setelah diturunkan.

Istilah ini hanya akan muncul di tingkat pertama atau dengan eksponen yang sama dengan 1. Kualitas ini membuatnya sepenuhnya jelas di bawah metode faktorisasi tradisional. Sehingga menjadi mungkin untuk mendapatkan ekspresi yang mendefinisikan diferensial dθ/dx.

Dalam aturan rantai, sifat progresif dari diferensiasi atau proses turunan ditampilkan. Dimana untuk fungsi komposit f [g (x)], ekspresi diferensial f harus menjadi

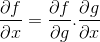
Pesanan operasional

Dalam setiap formula atau hukum derivasi yang diterapkan, urutan variabel harus diperhitungkan. Kriteria yang terkait dengan variabel independen dihormati, tanpa mengubah korelasinya dengan variabel dependen.

Rasio variabel dependen pada saat turunan diambil secara langsung.; Dengan pengecualian bahwa ini akan dianggap sebagai fungsi kedua, itulah sebabnya kriteria aturan rantai untuk fungsi campuran diterapkan.

Ini dapat dikembangkan dalam ekspresi dengan lebih dari 2 variabel. Di bawah prinsip yang sama, semua diferensial yang mengacu pada variabel dependen akan dilambangkan.

Dapat melayani Anda: apa pedomannya? (Geometri)

Secara grafis kriteria yang sama ditangani yang mendefinisikan turunannya. Sementara turunannya adalah kemiringan garis garis singgung ke kurva di bidang, sisa diferensial milik variabel dependen (dy/dx, dz/dx) mewakili bidang singgung ke badan vektor yang dijelaskan oleh fungsi beberapa variabel beberapa variabel.

Implisit dari suatu fungsi

Dikatakan bahwa fungsi secara implisit didefinisikan, jika ekspresi y = f (x) dapat direpresentasikan sebagai fungsi variabel ganda f (x, y) = 0 sedangkan f didefinisikan dalam bidang r².

3xy³ - 2y + xy² = x dan dapat ditulis dalam bentuk 3XY³ - 2y + xy² - Xy = 0

Mengingat ketidakmungkinan menjelaskan fungsi y = f (x).

Sejarah

Kalkulus diferensial mulai ditunjuk oleh berbagai peneliti matematika, sekitar abad ketujuh belas. Pertama kali disebutkan adalah melalui kontribusi Newton dan Leibniz. Keduanya memperlakukan kalkulus diferensial dari sudut pandang yang berbeda, tetapi menyatu dalam hasilnya.

Sementara Newton berfokus pada diferensiasi sebagai kecepatan atau laju variasi, pendekatan Leibniz lebih geometris. Dapat dikatakan bahwa Newton menyerang dugaan yang ditinggalkan oleh Apollonius dari Perge dan Leibniz Gagasan Geometris Fermat.

Derivasi implisit muncul segera ketika persamaan diferensial dan komprehensif dipertimbangkan. Mereka memperluas konsep geometris Leibniz ke R³ dan bahkan ruang multidimensi.

Aplikasi

Derivatif implisit digunakan dalam berbagai situasi. Mereka umum dalam masalah nilai tukar antara variabel terkait, di mana, tergantung pada rasa studi, variabel akan dianggap tergantung atau mandiri.

Mereka juga memiliki aplikasi geometris yang menarik, seperti dalam masalah refleksi atau bayangan, pada angka yang bentuknya dapat dimodelkan secara matematis.

Dapat melayani Anda: Kuota Pengambilan Sampel: Metode, Keuntungan, Kekurangan, Contoh

Mereka sering digunakan di bidang ekonomi dan teknik, serta dalam berbagai investigasi fenomena alam dan bangunan eksperimental.

Latihan terpecahkan

Latihan 1

Tentukan ekspresi implisit yang mendefinisikan dy/dx

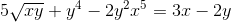
Setiap elemen berbeda dari ekspresi

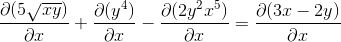
Menetapkan aturan rantai dalam setiap kasus yang kompeten

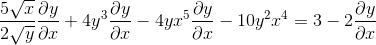
Pengelompokan di satu sisi kesetaraan elemen yang memiliki dy/dx

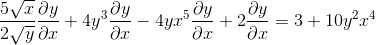
Adalah faktor yang menggunakan faktor umum

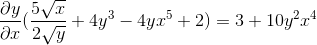
Dibersihkan dengan mendapatkan ekspresi yang dicari

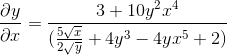
Latihan 2

Tentukan ekspresi implisit yang mendefinisikan dy/dx

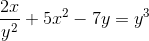
Mengekspresikan turunannya untuk dilakukan

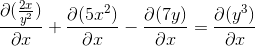
Secara implisit berasal sesuai dengan aturan rantai

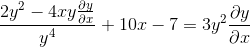
Memperhitungkan elemen umum

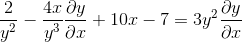
Mengelompokkan istilah dy/dx di satu sisi kesetaraan

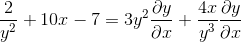
Faktor umum untuk elemen diferensial

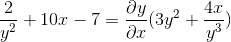
Kami jelas dan mendapatkan ekspresi yang dicari

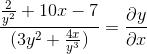
Referensi

1. Kalkulus variabel tunggal. Ron Larson, Bruce H. Edwards. Pembelajaran Cengage, 10 Nov. 2008
2. Teorema Fungsi Implisit: Sejarah, Teori, dan Aplikasi. Steven G. Krantz, Harold R. Taman. Sains Springer & Media Bisnis, 9 November. 2012
3. Analisis multivariabel. Sable Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13 Desember. 2010
4. Dinamika Sistem: Pemodelan, Simulasi, dan Kontrol Sistem Mekatronik. Dean c. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7 Mar. 2012
5. Kalkulus: Matematika dan Pemodelan. William Bauldry, Joseph R. Fiedler, Frank R.Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1 Januari. 1999