Perbedaan antara kecepatan dan kecepatan (dengan contoh)

Itu Perbedaan antara kecepatan dan kecepatan Ada, meskipun keduanya terkait jumlah fisik. Dalam bahasa umum satu istilah atau yang lain digunakan secara bergantian seolah -olah mereka identik, tetapi dalam fisika perlu membedakannya.

Dalam artikel ini kedua konsep didefinisikan, perbedaan ditunjukkan dan dijelaskan, dengan contoh, bagaimana dan kapan satu atau yang lain berlaku. Untuk menyederhanakan kami mempertimbangkan partikel yang bergerak dan dari sana kami akan meninjau konsep kecepatan dan kecepatan. 

	Kecepatan	Kecepatan
Definisi	Itu adalah jarak yang ditempuh per unit waktu.	Adalah perpindahan (atau perubahan posisi) di setiap unit waktu.
Notasi	v	v
Jenis objek matematika	Mendaki.	Vektor.
Formula (untuk periode waktu yang terbatas)*	v = ΔS/ΔT	v = ΔR/ΔT
Formula (untuk sekejap waktu tertentu) **	v = ds/dt = s '(t)	v = dr/dt = r '(t)
Penjelasan formula	*Panjang jalan yang ditempuh dibagi antara periode waktu yang digunakan untuk menempuhnya.** Dalam kecepatan sesaat, rentang waktu cenderung nol. ** Operasi matematika adalah turunan dari busur lintasan sebagai fungsi waktu sehubungan dengan waktu t waktu.	*Perpindahan vektor dibagi dengan periode waktu di mana perpindahan terjadi. ** Dalam kecepatan seketika periode waktu cenderung nol. ** Operasi matematika adalah turunan dari posisi tepat waktu.
Karakteristik	Untuk mengekspresikannya, hanya bilangan real positif yang diperlukan, terlepas dari dimensi spasial di mana gerakan terjadi. ** Kecepatan instan adalah nilai absolut dari kecepatan instan.	Lebih dari satu bilangan real (positif atau negatif) mungkin diperlukan untuk mengekspresikannya, tergantung pada dimensi spasial di mana pergerakan terjadi. ** Modul kecepatan instan secara instan.

Contoh dengan kecepatan seragam pada bagian lurus

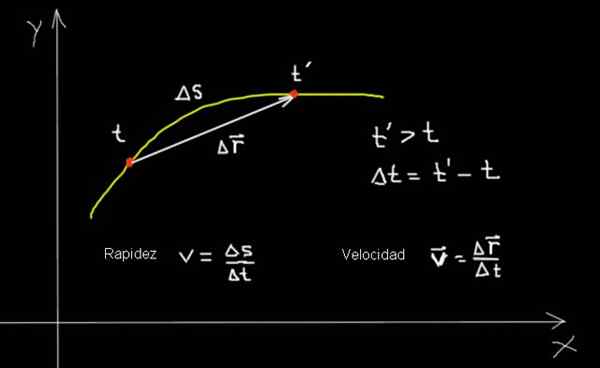
Kecepatan dan kecepatan partikel yang bergerak dalam kurva. Disiapkan oleh: f. Zapata.

Di tabel sebelumnya beberapa aspek kecepatan dan kecepatan dirangkum. Dan kemudian untuk melengkapi, beberapa contoh dipertimbangkan yang menggambarkan konsep yang terlibat dan hubungan mereka:

Dapat melayani Anda: paramagnetisme

- Contoh 1

Asumsikan bahwa semut merah bergerak mengikuti garis lurus dan ke arah yang ditunjukkan pada gambar berikut.

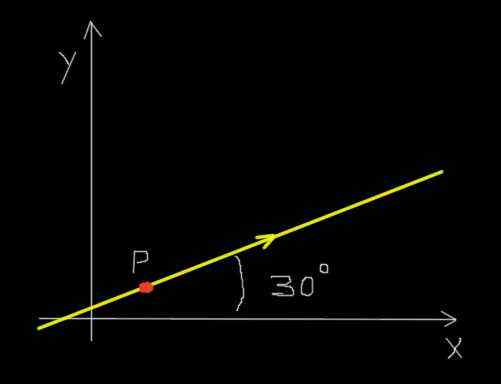Semut di jalan bujur. Sumber: f. Zapata.

Selain itu, semut bergerak secara seragam sehingga menempuh jarak 30 milimeter dalam periode waktu 0,25 detik. 

Tentukan kecepatan dan kecepatan semut.

Larutan 

Kecepatan semut dihitung dengan membagi jarak ΔS Tur Toure Δt.

V = ΔS/ΔT = (30 mm)/(0,25s) = 120 mm/s = 12 cm/s

Laju semut dihitung dengan membagi perpindahan ΔR antara periode waktu di mana perpindahan tersebut dilakukan.

Perpindahannya adalah 30 mm ke arah 30º sehubungan dengan sumbu x, atau dalam bentuk kompak: 

ΔR = (30 mm ¦ 30º)

Dapat dicatat bahwa perpindahan terdiri dari besarnya dan alamat, karena itu adalah kuantitas vektor. Atau, perpindahan dapat diekspresikan sesuai dengan komponen cartesian x dan y, dengan cara ini:

ΔR = (30 mm* cos (30º); 30 mm* tanpa (30º)) = (25,98 mm; 15,00 mm)

Tingkat semut dihitung dengan membagi perpindahan antara periode waktu di mana ia dilakukan:

v = ΔR/Δt = (25,98 mm / 0,25 detik; 15,00 mm / 0,25 s) = (103,92; 60,00) mm / s

Kecepatan ini dalam komponen Cartesian x dan y y dalam satuan cm/s adalah:

v = (10.392; 6.000) cm/s.

Atau, vektor kecepatan dapat diekspresikan dalam bentuk kutub (modul ¦ arah) seperti yang ditunjukkan:

v = (12 cm/s ¦ 30º).

Catatan: Dalam contoh ini karena kecepatannya konstan, kecepatan rata -rata dan kecepatan sesaat bertepatan. Terbukti bahwa modul kecepatan instan cepat.

Dapat melayani Anda: kepadatan

Contoh 2

Semut yang sama dari contoh sebelumnya berubah dari A ke B, setelah B ke C dan akhirnya dari C ke A, mengikuti jalur segitiga yang ditunjukkan pada gambar berikut.

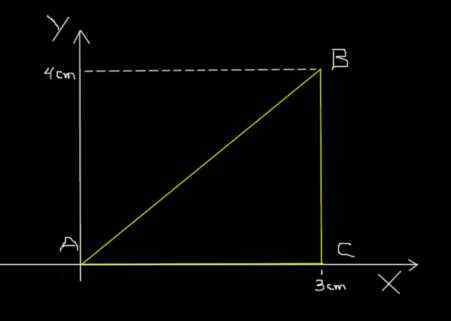Jalur segitiga semut. Sumber: f. Zapata.

Bagian AB melakukan perjalanan pada 0,2s; BC bergerak di 0,1s dan akhirnya CA bergerak di 0,3s. Hitung kecepatan rata -rata rute ABCA dan kecepatan rata -rata rute ABCA.

Larutan 

Untuk menghitung kecepatan rata -rata semut, kita mulai dengan menentukan jarak total yang ditempuh:

ΔS = 5 cm + 4 cm + 3 cm = 12 cm.

Periode waktu yang digunakan untuk seluruh perjalanan adalah:

Δt = 0,2S + 0,1S + 0,3S = 0,6 s.

Jadi, kecepatan rata -rata semut adalah:

V = ΔS/ΔT = (12 cm)/(0,6S) = 20 cm/s.

Kemudian kecepatan rata -rata semut pada rute ABCA dihitung. Dalam hal ini, perpindahan yang dilakukan oleh semut adalah:

ΔR = (0 cm; 0 cm)

Ini karena perpindahan adalah perbedaan antara posisi akhir lebih sedikit posisi awal. Karena kedua posisi itu sama, maka perbedaannya batal, menghasilkan perpindahan nol.

Perpindahan nol ini dilakukan dalam periode waktu 0,6 sehingga jenis rata -rata semut adalah:

v =(0 cm; 0 cm)/ 0.6s = (0; 0) cm/ s.

Kesimpulan: Kecepatan rata-rata 20 cm/s, Tapi kecepatan rata -rata adalah nol di rute ABCA.

Contoh dengan kecepatan seragam pada bagian melengkung

Contoh 3

Serangga bergerak pada lingkaran radius 0,2m dengan kecepatan seragam, sehingga mulai dari A dan mencapai B, ia bergerak ¼ dari lingkar pada 0,25 detik.

Dapat melayani Anda: pers hidrolik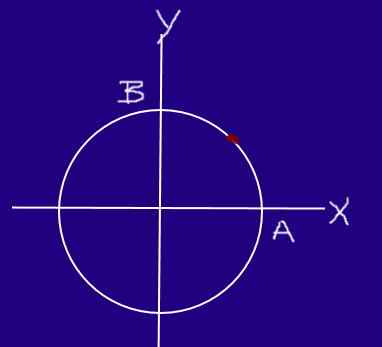Serangga bagian melingkar. Sumber: f. Zapata.

Tentukan kecepatan dan kecepatan serangga di bagian AB.

Larutan 

Panjang busur keliling antara A dan B adalah:

ΔS = 2πr /4 = 2π (0,2m) /4 = 0,32 m.

Menerapkan definisi kecepatan rata -rata yang Anda miliki:

V = ΔS/ΔT = 0,32 m/0,25 s = 1,28 m/s.

Untuk menghitung kecepatan rata -rata, perlu untuk menghitung vektor perpindahan antara posisi awal A dan b terakhir:

ΔR = (0; r)-(r; 0) = (-r; r) = (-0.2; 0.2) m

Menerapkan definisi kecepatan rata -rata diperoleh:

v = ΔR/ Δt = (-0.2; 0.2) m / 0.25s = (-0.8; 0.8) m/s.

Ekspresi sebelumnya adalah kecepatan rata -rata antara A dan B yang diekspresikan dalam bentuk cartesian. Atau kecepatan rata -rata dapat diekspresikan dalam bentuk kutub, yaitu modul dan arah:

| v | = ((-0.8)^2 + 0.8^2)^(½) = 1.13 m/s

Alamat = arctan (0.8 / (-0.8)) = arcan (-1) = -45º + 180º = 135º sehubungan dengan sumbu x.

Akhirnya, vektor kecepatan rata -rata dalam bentuk kutub adalah: v =(1.13 m/s ¦ 135º).

Contoh 4

Dengan asumsi bahwa momen awal dari serangga dari contoh sebelumnya adalah 0s dari titik A, posisi vektor Anda adalah instan apa pun yang diberikan oleh:

R(t) = [r cos ((π/2) t); R sen ((π/2) t)].

Tentukan kecepatan dan kecepatan instan untuk setiap saat t.

Larutan 

Kecepatan sesaat adalah turunan sehubungan dengan waktu posisi:

v(t) = DR/dt = [-r (π/2) tanpa ((π/2) t); R (π/2) cos ((π/2) t)]]

Kecepatan instan adalah modul kecepatan instan vektor:

v (t) = | v(T) | = π r / 2^½

Referensi

1. Alonso m., Finn e. Volume Fisika I: Mekanika. 1970. Dana Pendidikan Inter -American S.KE.
2. Hewitt, hlm. Ilmu Fisik Konseptual. Edisi Kelima. Pearson.
3. Muda, Hugh. Fisika Universitas dengan Fisika Modern. Edisi ke -14. Pearson.
4. Wikipedia. Kecepatan. Pulih dari: is.Wikipedia.com
5. Zita, a. Perbedaan antara kecepatan dan kecepatan. Diperoleh dari: diferensiator.com