Simbol dan formula diameter, cara mengeluarkannya, keliling

Dia diameter Itu adalah garis lurus yang melewati pusat kurva datar tertutup atau sosok dalam dua atau tiga dimensi dan yang juga bergabung dengan titik yang berlawanan. Biasanya lingkaran (kurva datar), lingkaran (gambar datar), bola atau silinder melingkar lurus (objek tiga dimensi).

Meskipun keliling dan lingkaran biasanya dianggap sebagai sinonim, ada perbedaan antara kedua istilah. Lingkar adalah kurva tertutup yang melingkupi lingkaran, yang memenuhi kondisi bahwa jarak antara titik mana pun dan pusatnya adalah sama. Jarak ini tidak lain adalah jari -jari keliling. Sebaliknya, lingkaran adalah sosok datar yang dibatasi oleh lingkar.

Gambar 1. Diameter roda sepeda adalah fitur penting dalam desainnya. Sumber: Pixabay.

Dalam hal keliling, lingkaran dan bola, diameter adalah segmen lurus yang berisi setidaknya tiga titik: pusat ditambah dua titik tepi lingkar atau lingkaran, atau permukaan bola.

Dan untuk silinder melingkar lurus, diameter mengacu pada penampang, yang bersama -sama dengan tinggi, adalah dua parameter karakteristiknya.

Diameter keliling dan lingkaran, dilambangkan dengan Ø atau hanya huruf "d" atau "d", terkait dengan perimeter, kontur atau panjangnya, yang dilambangkan dengan huruf l:

L = π.D = π. salah satu

Setiap kali Anda memiliki keliling, hasil bagi antara panjangnya dan diameternya adalah bilangan irasional π = 3.14159 ..., dengan cara ini:

π = l/d

[TOC]

Bagaimana mendapatkan diameternya?

Ketika gambar keliling atau lingkaran tersedia, atau secara langsung objek melingkar, seperti mata uang atau cincin misalnya, sangat mudah untuk mengambil diameter dengan aturan. Anda hanya perlu memastikan bahwa tepi aturan pada saat yang sama memiliki dua titik keliling dan pusat yang sama.

Dapat melayani Anda: aljabar

Kaki kaliber, vernier atau kaki raja sangat cocok untuk mengukur diameter eksternal dan internal dalam koin, lingkaran, cincin, kacang -kacangan, tabung dan banyak lagi.

Gambar 2. Vernier Digital Mengukur Diameter Koin. Sumber: Pixabay.

Jika alih -alih objek atau gambarnya, Anda memiliki data seperti radio R, Kemudian mengalikan dengan 2 Anda memiliki diameter. Dan jika panjang atau perimeter lingkar diketahui, diameternya juga dapat diketahui, dengan izin:

D = 2.R
D = l / π

Cara lain untuk mendapatkan diameter adalah dengan mengetahui area lingkaran, permukaan bola, penampang silinder, area melengkung ini atau volume bola atau silinder. Itu semua tergantung pada sosok geometris mana itu. Misalnya, diameternya terlibat dalam area dan volume berikut:

-Area lingkaran: π.(D/2)²
-Area Permukaan Bola: 4π.(D/2)²
-Volume bola: (4/3) π.(D/2)³
-Volume silinder melingkar lurus: π.(D/2)².H (h adalah tinggi silinder)

Angka lebar konstan

Lingkaran adalah sosok datar yang konstan lebar, karena di mana pun terlihat, lebarnya diameter D. Namun, ada tokoh lain yang mungkin kurang dikenal yang lebarnya juga konstan.

Pertama mari kita lihat apa yang dipahami dengan lebar gambar: itu adalah jarak antara dua garis paralel -Sport sendi -, yang pada gilirannya tegak lurus dengan arah yang diberikan dan yang memenjarakan gambar, seperti yang ditunjukkan pada gambar kiri:

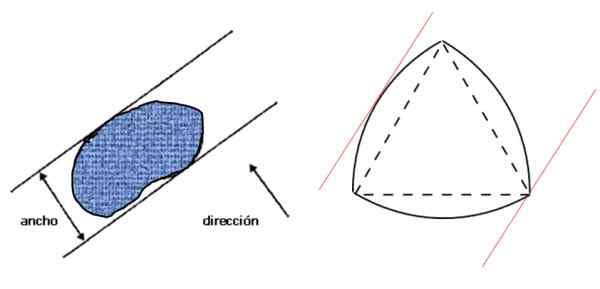Gambar 3. Lebar sosok datar (kiri) dan segitiga reuleaux, sosok lebar konstan (kanan). Sumber: f. Zapata.

Kemudian ke kanan adalah segitiga reuleaux, yang merupakan sosok lebar konstan dan yang memenuhi kondisi yang ditentukan pada gambar kiri. Jika lebar angka adalah D, perimeternya diberikan oleh teorema Barbier:

Dapat melayani Anda: perkiraan pengukuran figur amorf: contoh dan olahraga

L = π.D

The Sewers of City of San Francisco di California berbentuk seperti segitiga Reuleaux, dinamai oleh insinyur Jerman Franz Reuleaux (1829 - 1905). Dengan cara ini tapas tidak dapat jatuh ke lubang dan menghabiskan lebih sedikit bahan untuk memproduksinya, karena area mereka kurang dari lingkaran:

A = (1- √3).πd² = 0.705.D²

Sedangkan untuk lingkaran:

A = π.(D/2)² = (π/4) D²= 0.785.D²

Tapi segitiga ini bukan satu -satunya sosok lebar yang konstan. Panggilan bisa dibangun Poligon Reuleaux dengan poligon lain yang memiliki nomor sisi yang aneh.

Diameter lingkar

Pada gambar berikutnya adalah unsur -unsur keliling, didefinisikan sebagai berikut:

Tali: segmen garis yang bergabung dengan dua titik lingkar. Pada gambar adalah tali yang bergabung dengan titik C dan D, tetapi string tak terbatas dapat ditelusuri unik setiap titik poin dari lingkar.

Diameter: Ini adalah tali yang melewati pusat, bergabung dengan dua titik keliling dengan pusat atau. Itu adalah tali terlama dari lingkar, karena alasan itu disebut "tali utama".

Radio: segmen garis yang bergabung dengan pusat dengan titik lingkar mana pun. Nilainya, seperti diameternya, konstan.

Lingkar: Ini adalah himpunan semua poin yang menyamakan atau.

Busur: Ini didefinisikan sebagai segmen keliling yang dibatasi oleh dua radio (tidak digambar pada gambar).

Gambar 4. Bagian dari lingkar, termasuk diameter, yang melewati pusat. Sumber: Wikimedia Commons.

- Contoh 1

Persegi panjang yang ditampilkan berukuran 10 inci, yang ketika berliku membentuk silinder melingkar lurus yang diameternya 5 inci. Jawab pertanyaan berikut:

Itu dapat melayani Anda: acara yang saling eksklusif: properti dan contoh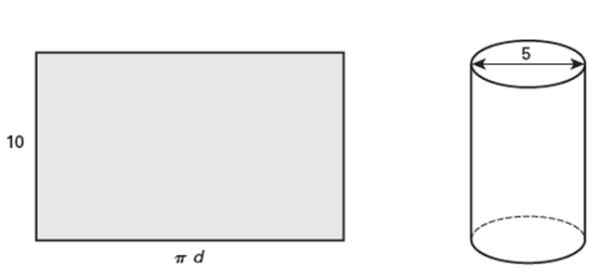Gambar 5. Persegi panjang yang digulung menjadi silinder melingkar lurus. Sumber: Jiménez, R. Matematika II. Geometri dan Trigonometri. 2nd. Edisi. Pearson.

a) Apa kontur tabung?
b) Temukan area persegi panjang
c) Hitung area cross -bagian silinder.

Solusi untuk

Kontur tabung adalah L = π.D = 5π PLG = 15.71 PLG.

Solusi b

Area persegi panjang adalah Dasar X Tinggi, Menjadi dasar L sudah dihitung dan tinggi adalah 10 PLG menurut pernyataan, oleh karena itu:

A = 15.71 PLG x 10 PLG = 157.1 PLG².

Solusi c

Akhirnya, area yang diminta dihitung sebagai berikut:

A = π.(D/2)² = (π/4) D² = (π/4) x (5 PLG)²= 19.63 PLG².

- Contoh 2

Hitung area teduh pada Gambar 5a. Kotak memiliki sisi l.

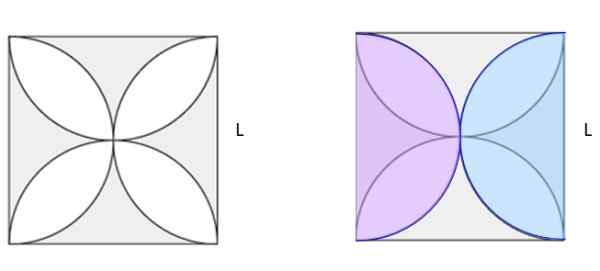Gambar 6. Temukan area teduh di gambar kiri. Jiménez, r. Matematika II. Geometri dan Trigonometri. 2nd. Edisi. Pearson.

Larutan

Pada Gambar 5b, dua setengah lingkaran identik ukuran warna merah muda dan biru telah ditarik, ditumpangkan pada sosok asli. Di antara mereka mereka membuat lingkaran lengkap. Jika kuadrat kuadrat dihitung dan area lingkaran dikurangi, itu membuat area teduh pada Gambar 5b. Dan terlihat bagus, ternyata itu adalah setengah dari area teduh di 5a.

-Area Square: L²
-Diameter semi -lingkaran: l
-Area Lingkaran: π.(L/2)²= (π/4) l²
-Perbedaan area = setengah dari area teduh =

L² - (π/4) l² = [(4 - π)/4] l²= 0.2146 l²

-Area teduh = 2 x 0.2146 l²= 0.4292l2

Berapa banyak diameter yang dimiliki keliling?

Diameter tak terbatas dapat ditarik dalam lingkaran, dan salah satu dari mereka mengukur hal yang sama.

Referensi

1. Antonio. Segitiga reuleaux dan kurva lebar konstan lainnya. Pulih dari: diseminator.com.
2. Baldor, a. 2002. Geometri datar dan ruang dan trigonometri. Kelompok tanah air budaya.
3. Jiménez, r. Matematika II. Geometri dan Trigonometri. 2nd. Edisi. Pearson.
4. Wikipedia. Segitiga Reuleaux. Pulih dari: itu.Wikipedia.org.
5. Wolfram Mathworld. Diameter. Dipulihkan dari: MathWorld.Wolfram.com.