Budaya dan Masyarakat Umum

Distribusi eksponensial

1547
400
Irvin Reichel

Kami menjelaskan apa itu distribusi eksponensial, karakteristiknya, formula, contoh dan latihan terpecahkan

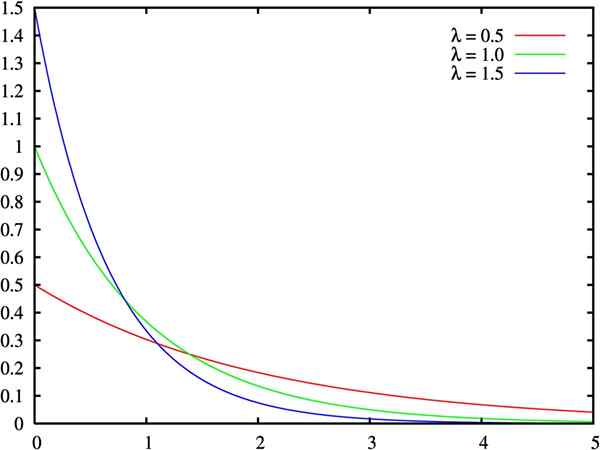
Grafik fungsi kepadatan distribusi eksponensial, untuk tiga nilai parameter lambda. Sumber: Wikimedia Commons.

Apa itu distribusi eksponensial?

Itu distribusi eksponensial Ini adalah model probabilistik untuk variabel acak kontinu. Ini berarti bahwa, melalui itu, Anda dapat mengetahui probabilitas terjadinya nilai variabel tertentu, sehingga merupakan distribusi probabilitas.

Untuk mendapatkan distribusi, itu dimulai dari a fungsi kepadatan, yang memiliki bentuk parameter eksponensial λ> 0:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ text Ya x \ leq 0 \ End case$

Fungsi kepadatan seperti itu tidak memungkinkan menghitung probabilitas, tetapi setelah ditetapkan f (x), fungsi distribusi f (x), yang dengannya probabilitas diperoleh, diperoleh dengan integrasi f (x). Misalnya, probabilitas p bahwa variabel acak mengambil nilai antara 0 dan x adalah:

$F(x)=P[x\leq x]=\int_0^xf(x)dx$

Melaksanakan integrasi, yang sangat sederhana, karena integral dari suatu eksponensial adalah eksponensial yang sama, kecuali untuk konstanta yang menyertai argumen, diperoleh:

$F(x)=\int_0^x\lambda e^-\lambda xdx=\lambda \left (-\frac1\lambda \right )\left [ e^-\lambda x \right ]_0^x=-\left (e^-\lambda x-e^0 \right )=1-e^-\lambda x$

Distribusi eksponensial banyak digunakan untuk menentukan probabilitas suatu peristiwa setelah waktu tunggu tertentu, seperti waktu yang terjadi dalam kemunculan rumah sakit sebelum pasien tiba.

Seringkali, peristiwa mengacu pada kegagalan atau kerusakan jenis listrik, elektronik dan lainnya. Dalam hal ini, distribusi eksponensial membantu memperkirakan waktu yang dibutuhkan komponen untuk gagal, dan juga waktu di antara perbaikan. Ini dikenal sebagai teori reliabilitas.

Karakteristik distribusi eksponensial

Beberapa fitur yang paling menonjol dari fungsi kepadatan F (x) dari distribusi eksponensial adalah sebagai berikut:

f (x) positif.
Area di bawah kurva y = f (x) = λe^−λ^X Itu selalu sama dengan 1, karena jumlah probabilitas terjadinya semua nilai variabel harus 1. Ini adalah syarat yang dipenuhi fungsi kepadatan. Area ini dihitung melalui integral:

Dapat melayani Anda: anuma

$\int_-\infty ^\infty f(x)dx=\int_-\infty ^\infty \lambda e^-\lambda xdx=1$

Kurangnya memori distribusi eksponensial

Fitur yang paling menonjol dari distribusi eksponensial adalah kurangnya memori. Sebagai contoh, misalkan waktu berlalu adalah pemodelan dengan distribusi ini sampai kegagalan elemen terjadi.

Nah, kurangnya memori mengacu pada mengetahui bahwa elemen tersebut bekerja untuk waktu bertahan hidup "S", tidak memodifikasi probabilitas bahwa elemen akan terus berjalan hingga jumlah tambahan waktu tertentu "T".

Yaitu, probabilitas bahwa elemen gagal dari sini hingga waktu tertentu (1 menit, 1 jam, misalnya) tidak bergantung pada telah bekerja dengan baik sejauh ini.

Secara matematis dihitung dengan definisi probabilitas peristiwa independen:

$P[x\geq s+t/x\geq s]=\fracP[x\geq s+t]P[x\geq s]=\frac1-F(s+t)1-F(s)=\frac1- [1-e^-\lambda (s+t) ]1- [1-e^-\lambda s ]= \beginmatrix \\ \endmatrix$

$=e^-\lambda t$

Oleh karena itu, probabilitas tidak tergantung pada waktu S atau bertahan hidup.

Rumus

1.- Fungsi kepadatan dari distribusi eksponensial adalah:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ text Ya x \ leq 0 \ End case$

Dimana λ adalah parameter distribusi.

2.- Seperti dijelaskan di atas, distribusi probabilitas itu sendiri dilambangkan sebagai f (x) dan probabilitas yang berbeda diperoleh dengan integrasi fungsi kepadatan:

$F(x)=\begincases 0 & \text si x\leq 0 \\ 1-e^-\lambda x& \text si x>0 \ End case$

3.- Dari yang di atas itu mengikuti bahwa probabilitas bahwa variabel mengambil nilai kurang dari atau sama dengan "x" adalah p [x≤x] = 1 −e^−λ^X.

4.- Area di bawah kurva y = f (x), termasuk antara A dan B memungkinkan untuk menghitung probabilitas bahwa variabel dalam interval [a, b]. Area ini adalah:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- Nilai p [x ≥ a] adalah 1 - f (a) = 1 - (1 - e^−λ^X) = e^−λ^X

Nilai yang diharapkan dari distribusi eksponensial

Harapan atau nilai yang diharapkan E (x) dari distribusi eksponensial adalah nilai yang diharapkan terjadi lebih sering. Itu dihitung dari integral:

Dapat melayani Anda: teknik pendaftaran informasi

$E(x)=\int_0^\infty xf(x)dx$ Yang mudah diselesaikan dengan metode integrasi oleh bagian. Hasilnya adalah:

E (x) = 1/λ

Varian distribusi eksponensial

Untuk perhitungan varians, integral harus ditentukan:

$Var(x)=\int_0^\infty x^2f(x)dx$

Yang juga diselesaikan dengan metode integrasi oleh bagian, untuk mendapatkan:

Var (x) = 1/λ²

Kekhasan distribusi eksponensial adalah bahwa standar deviasi S (x), didefinisikan sebagai akar kuadrat dari varian adalah:

S (x) = √var (x) = √ (1/λ²) = 1/λ

Yaitu, standar deviasi sama dengan harapan distribusi.

Contoh distribusi eksponensial

Data sampel karbon 14

Distribusi eksponensial digunakan untuk menentukan waktu yang diperlukan untuk menghancurkan partikel radioaktif. Waktu ini digunakan untuk tanggal sampel fosil dengan radiokarbon.

Waktu yang dibutuhkan untuk memeriksa surat

Anda dapat memodelkan waktu yang diambil pengguna untuk meninjau email mereka, setelah pemberitahuan telah diterima, melalui distribusi eksponensial. Misalkan parameter distribusi adalah λ = 0.2, kemudian, probabilitas bahwa seseorang membutuhkan waktu kurang dari 1 menit untuk meninjau emailnya adalah:

$P[x\leq 1]=\int_0^1f(x)dx=\int_0^10.2e^-0.2xdx$

Integral ini diselesaikan pada awalnya, hanya tetap untuk menggantikan nilai numerik dalam solusi dan menghitung hasil akhir:

P [x ≤ 1] = 1 --e^-^0.2^×¹ = 1− e^-^0.2 = 1− 0.819 = 0.181

Ini juga dapat secara langsung diganti pada fungsi f (x) yang diberikan di atas, untuk mendapatkan f (1).

Latihan

Latihan 1

Temukan probabilitas bahwa seseorang kemudian satu jam meninjau email mereka, jika distribusi probabilitas adalah eksponensial, dengan parameter λ = 0.2.

Larutan

P [x ≥ 60] harus dihitung, karena 1 jam setara dengan 60 menit dan probabilitas orang yang terlambat 60 menit atau lebih untuk memeriksa surat diminta. Probabilitas dihitung dengan integral yang sama yang disajikan pada awalnya, hanya mengubah batas integrasi:

Dapat melayani Anda: Rapa Nui: Sejarah, Karakteristik, Budaya, Tradisi

$P[x\geq 60]=\int_60^\infty 0.2e^-0.2xdx=-\left ( -e^-0.2\times 60 \right )=0.000006144$

Nilai yang diperolehnya kecil, jadi sangat tidak mungkin bahwa seseorang membutuhkan waktu lebih dari satu jam untuk meninjau email mereka.

Latihan 2

Lampu listrik biasanya memiliki durasi yang terbatas, kecuali umbi stasiun pemadam kebakaran yang terkenal di Livermore, California, yang tidak pernah gagal sejak itu untuk pertama kalinya, pada tahun 1901.

Asumsikan bahwa durasi bohlam saat ini mengikuti distribusi eksponensial, dengan nilai yang diharapkan dari 8 bulan. Menghitung:

a) Berapa probabilitas bahwa bohlam akan berlangsung antara 5 dan 14 bulan?

b) Probabilitas bahwa bohlam akan bertahan lebih dari 25 bulan, mengetahui bahwa ia memiliki lebih dari 11 bulan beroperasi.

Solusi untuk

Hal pertama adalah menemukan nilai λ, melalui nilai yang diharapkan dari distribusi e (x) = 8 bulan. Menurut apa yang dikatakan di bagian sebelumnya, nilai yang diharapkan adalah kebalikan dari parameter λ, oleh karena itu: oleh karena itu:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Kemudian probabilitas yang diminta dihitung, dengan cara integral yang diberikan di awal, tetapi dengan mudah mengubah batas integrasi:

Kemudian diganti dalam fungsi f (x) yang diberikan di bagian sebelumnya, sebagai berikut:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Solusi b

Untuk menjawab masalah ini, properti kurangnya memori akan digunakan, diucapkan di atas. Seperti diketahui bahwa itu telah berlangsung lebih dari 11 bulan, lalu:

S = 11 bulan

Waktu tambahan untuk 25 bulan terakhir atau lebih adalah:

T = 14 bulan

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{−0.125 × 14}= 0.174