Distribusi karakteristik dan latihan diselesaikan

Itu distribusi f o Distribusi Fisher-Snedecor adalah apa yang digunakan untuk membandingkan varian dua populasi yang berbeda atau independen, yang masing-masing mengikuti distribusi normal.

Distribusi yang mengikuti varian satu set sampel populasi normal tunggal adalah distribusi Ji-square (Χ²) derajat n-1, jika masing-masing sampel set memiliki elemen N.

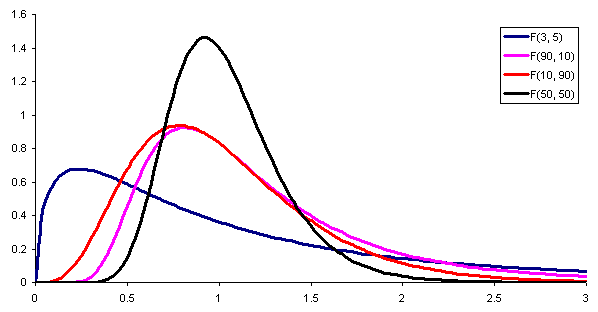
Gambar 1. Berikut adalah kepadatan probabilitas dari distribusi F dengan kombinasi parameter (atau derajat kebebasan) yang berbeda dari pembilang dan penyebut masing -masing. Sumber: Wikimedia Commons.

Untuk membandingkan varian dari dua populasi yang berbeda, perlu untuk mendefinisikan a statistik, artinya variabel acak tambahan yang memungkinkan untuk membedakan apakah kedua populasi memiliki atau tidak varian yang sama.

Variabel tambahan ini dapat langsung menjadi hasil bagi varian sampel dari masing -masing populasi, dalam hal ini, jika quotient tersebut dekat dengan unit, dibuktikan bahwa kedua populasi memiliki varian yang sama.

[TOC]

Statistik f dan distribusi teoretisnya

Variabel acak F atau statistik F yang diusulkan oleh Ronald Fisher (1890 - 1962) yang lebih sering digunakan untuk membandingkan varian dua populasi dan didefinisikan sebagai berikut:

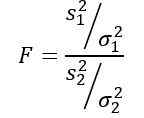
Menjadi s² Varian sampel dan σ² Varians populasi. Untuk membedakan masing -masing dari dua kelompok populasi, langganan 1 dan 2 masing -masing digunakan.

Diketahui bahwa distribusi Ji-square dengan (N-1) derajat kebebasan adalah yang mengikuti variabel tambahan (atau statistik) yang didefinisikan di bawah ini:

X² = (N-1) s² / σ².

Oleh karena itu, statistik F mengikuti distribusi teoretis yang diberikan oleh formula berikut:

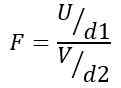
Makhluk ATAU Distribusi ji-square dengan D1 = n1 - 1 derajat kebebasan untuk populasi 1 dan V Distribusi ji-square dengan D2 = n2 - 1 derajat kebebasan untuk populasi 2.

Dapat melayani Anda: aljabar vektor

Rasio yang didefinisikan dengan cara ini adalah distribusi probabilitas baru, yang dikenal sebagai distribusi f dengan D1 derajat kebebasan di pembilang dan D2 derajat kebebasan dalam penyebut.

Rata -rata, mode dan varian distribusi f

Setengah

Distribusi rata -rata f dihitung sebagai berikut:

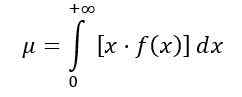
Menjadi f (x) Kepadatan probabilitas distribusi f, yang ditunjukkan pada Gambar 1 untuk beberapa kombinasi parameter atau derajat kebebasan.

Anda dapat menulis kepadatan probabilitas f (x) tergantung pada fungsi γ (fungsi gamma):

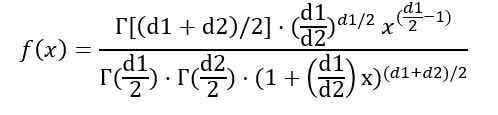
Setelah integral yang ditunjukkan sebelumnya, disimpulkan bahwa rata -rata distribusi F dengan derajat kebebasan (d1, d2) adalah: is: is: is: is: is: is: is: is: is: is: is:

μ = d2 / (d2 - 2) dengan d2> 2

Di mana itu menunjukkan bahwa, anehnya, rata -rata tidak tergantung pada derajat kebebasan D1 dari pembilang.

Mode

Di sisi lain, fashion tidak bergantung pada D1 dan D2 dan diberikan oleh:

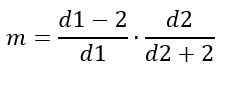
Untuk d1> 2.

Varian distribusi f

Varians σ² distribusi f dihitung dari integral:

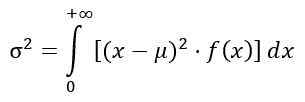
Memperoleh:

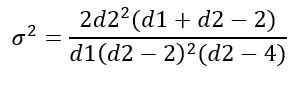
Manajemen distribusi f

Seperti distribusi probabilitas kontinu lainnya yang melibatkan fungsi yang rumit, manajemen distribusi F dilakukan dengan tabel atau perangkat lunak.

Tabel distribusi f

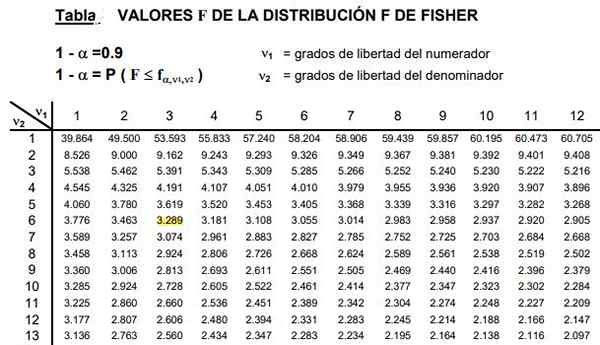Gambar 2. Bagian dari tabel distribusi F ditampilkan, yang biasanya sangat luas karena ada kombinasi luas dari kemungkinan derajat kebebasan D1 dan D2.

Tabel melibatkan dua parameter atau derajat kebebasan distribusi f, kolom menunjukkan tingkat kebebasan pembilang dan baris tingkat kebebasan penyebut.

Dapat melayani Anda: Ketimpangan segitiga: demonstrasi, contoh, latihan terpecahkan

Gambar 2 menunjukkan bagian tabel distribusi F untuk kasus a tingkat signifikansi 10%, yaitu α = 0,1. Nilai f disorot saat d1 = 3 dan d2 = 6 dengan tingkat kepercayaan diri 1- α = 0,9 yaitu 90%.

Perangkat lunak untuk distribusi f

Adapun perangkat lunak yang mengelola distribusi f ada variasi yang hebat, dari spreadsheet sebagai Unggul bahkan paket khusus seperti Minitab, SPSS Dan R Untuk menyebutkan beberapa yang paling terkenal.

Perlu dicatat bahwa perangkat lunak geometri dan matematika Geogebra Ini memiliki alat statistik yang mencakup distribusi utama, termasuk distribusi f. Gambar 3 menunjukkan distribusi f untuk kasus d1 = 3 dan d2 = 6 tingkat kepercayaan diri 90%.

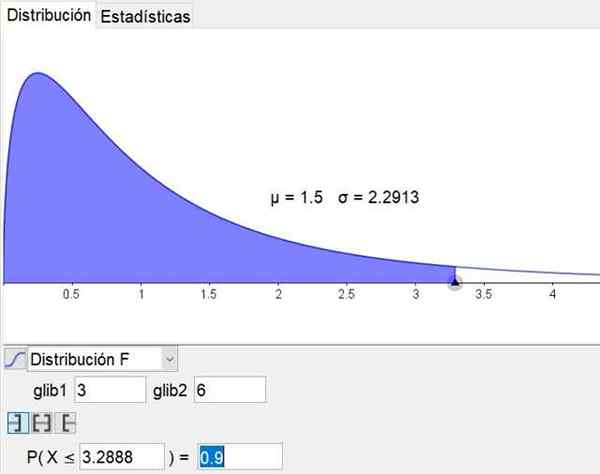Gambar 3. Distribusi F ditunjukkan untuk kasus D1 = 3 dan D2 = 6 dengan tingkat kepercayaan 90%, diperoleh melalui alat statistik Geogebra. Sumber: Geogebra.org

Latihan terpecahkan

Latihan 1

Pertimbangkan dua sampel populasi yang memiliki varian populasi yang sama. Jika sampel 1 adalah ukuran n1 = 5 dan sampel 2 adalah ukuran n2 = 10, tentukan probabilitas teoritis bahwa rasio varian masing -masing kurang dari atau sama dengan 2.

Larutan

Harus diingat bahwa statistik f didefinisikan sebagai:

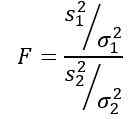
Tetapi kita diberitahu bahwa varian populasi sama, jadi untuk latihan ini berlaku:

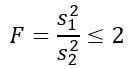
Karena Anda ingin mengetahui probabilitas teoretis bahwa rasio varian sampel ini kurang dari atau sama dengan 2, kita perlu mengetahui area di bawah distribusi F antara 0 dan 2, yang dapat diperoleh dengan tabel atau perangkat lunak. Untuk ini, harus diperhitungkan bahwa distribusi yang diperlukan f memiliki d1 = n1 - 1 = 5 - 1 = 4 dan d2 = n2 - 1 = 10 - 1 = 9, yaitu distribusi f dengan derajat kebebasan (4, 9).

Itu dapat melayani Anda: serangkaian kekuatan: contoh dan latihan

Dengan menggunakan alat statistik Geogebra Ditentukan bahwa area ini adalah 0.82, jadi disimpulkan bahwa probabilitas bahwa rasio varian sampel kurang dari atau sama dengan 2 adalah 82%.

Latihan 2

Ada dua proses pembuatan lembar tipis. Variabilitas ketebalan harus sebanyak mungkin. 21 Sampel dari setiap proses diambil. Sampel proses memiliki standar deviasi 1,96 mikron, sedangkan proses B memiliki standar deviasi 2,13 mikron. Proses mana yang memiliki variabilitas lebih rendah? Gunakan tingkat penolakan 5%.

Larutan

Data adalah sebagai berikut: SB = 2.13 dengan NB = 21; SA = 1,96 dengan Na = 21. Ini berarti bahwa Anda harus bekerja dengan distribusi F (20, 20) derajat kebebasan.

Hipotesis nol menyiratkan bahwa varian populasi dari kedua proses adalah identik, yaitu, σA^2 / σB^2 = 1. Hipotesis alternatif akan menyiratkan varian populasi yang berbeda.

Kemudian, dengan asumsi varian populasi yang identik, statistik f dihitung sebagai: fc = (sb/sa)^2 didefinisikan.

Karena tingkat penolakan telah diambil sebagai α = 0,05, maka α/2 = 0,025

Distribusi f (0.025; 20,20) = 0,406, sedangkan f (0.975; 20,20) = 2.46.

Oleh karena itu, hipotesis nol akan benar jika f yang dihitung sesuai: 0,406≤fc≤2,46. Kalau tidak, hipotesis nol ditolak.

Sebagai fc = (2,13/1.96)^2 = 1.18 Disimpulkan bahwa statistik FC berada dalam kisaran penerimaan hipotesis nol dengan kepastian 95%. Dengan kata lain dengan kepastian 95%, kedua proses manufaktur memiliki varian populasi yang sama.

Referensi

1. F Tes untuk Kemerdekaan. Pulih dari: saylordotorg.GitHub.Io.
2. Gelombang med. Statistik diterapkan pada ilmu kesehatan: Tes f. Pulih dari: medwave.Cl.
3. Probabilitas dan statistik. Distribusi f. Diperoleh dari: Probabilitas dan Estics.com.
4. Triola, m. 2012. Statistik dasar. 11. Edisi. Addison Wesley.
5. Unam. Distribusi f. Dipulihkan dari: Penasihat.Cuautitlan2.Unam.MX.
6. Wikipedia. Distribusi f. Pulih dari: is.Wikipedia.com