Matematika

Ukuran variabilitas

Ukuran variabilitas
Gambar 1.- Ukuran variabilitas paling terkenal. Sumber: f. Zapata.

Apa ukuran variabilitas?

Itu Ukuran variabilitas, Juga disebut langkah -langkah dispersi, mereka adalah indikator statistik yang menunjukkan seberapa dekat atau jauhnya data rata -rata aritmatika mereka ditemukan. Jika data mendekati rata -rata, distribusi terkonsentrasi, dan jika mereka jauh, itu maka distribusi yang tersebar.

Ada banyak langkah variabilitas, di antara yang paling terkenal adalah:

  • Jangkauan
  • Penyimpangan rata -rata
  • Perbedaan
  • Deviasi standar

Langkah -langkah ini melengkapi langkah -langkah kecenderungan pusat dan diperlukan untuk memahami distribusi data yang diperoleh dan mengekstrak informasi sebanyak mungkin.

Jangkauan

Kisaran atau rute mengukur amplitudo set data. Untuk menentukan nilainya, perbedaan antara nilai tertinggi X ditemukanMax dan nilai x terkecilMin:

R = xMax - XMin

Jika data tidak longgar tetapi dikelompokkan berdasarkan interval, maka kisaran dihitung dengan perbedaan antara batas atas interval terakhir dan batas bawah interval pertama.

Ketika kisaran adalah nilai kecil, itu berarti bahwa semua data cukup dekat satu sama lain, tetapi rentang besar menunjukkan bahwa ada banyak variabilitas. Jelaslah bahwa, terlepas dari batas atas dan batas bawah data, kisaran tidak memperhitungkan nilai -nilai di antara mereka, sehingga tidak disarankan untuk menggunakannya ketika nomor data besar.

Namun, ini merupakan ukuran langsung untuk menghitung dan memiliki unit data yang sama, jadi mudah untuk menafsirkannya.

Contoh peringkat

Selanjutnya, daftar ini tersedia dengan jumlah gol yang ditandai selama akhir pekan, di liga sepak bola dari sembilan negara:

Dapat melayani Anda: apa saja pembagi 30? (Penjelasan)

40, 32, 35, 36, 37, 31, 37, 29, 39

Ini adalah kumpulan data tanpa pengelompokan. Untuk menemukan jangkauannya, mereka melanjutkan untuk memesannya dari yang paling kecil ke yang terbesar:

29, 31, 32, 35, 36, 37, 37, 39, 40

Data dengan nilai tertinggi adalah 40 gol dan yang dengan nilai terendah adalah 29 gol, oleh karena itu kisarannya adalah:

R = 40−29 = 11 gol.

Dapat dipertimbangkan bahwa kisarannya kecil dibandingkan dengan data nilai minimum, yaitu 29 tujuan, sehingga dapat diasumsikan bahwa data tidak memiliki variabilitas yang besar.

Penyimpangan rata -rata

Ukuran variabilitas ini dihitung melalui rata -rata nilai absolut penyimpangan sehubungan dengan rata -rata. Menunjukkan deviasi rata -rata sebagai dM, Untuk data yang tidak dikelompokkan, deviasi rata -rata dihitung dengan rumus berikut:

Di mana n adalah jumlah data yang tersedia, xyo Ini mewakili setiap data dan x̄ adalah rata -rata, yang ditentukan dengan menambahkan semua data dan membagi antara n:

Deviasi rata -rata memungkinkan untuk mengetahui, rata -rata, berapa banyak unit data yang menyimpang dari rata -rata aritmatika dan memiliki keuntungan memiliki unit yang sama dengan data yang bekerja dengannya.

Contoh penyimpangan tengah

Menurut data kisaran, jumlah tujuan yang ditandai adalah:

40, 32, 35, 36, 37, 31, 37, 29, 39

Jika Anda ingin menemukan deviasi D sedangM Dari data ini, perlu untuk pertama -tama menghitung rata -rata aritmatika x̄:

Dan sekarang nilai x̄ diketahui, kami melanjutkan untuk menemukan deviasi rata -rataM:

= 2.99 ≈ 3 gol

Oleh karena itu dapat dikatakan bahwa, rata -rata, data bergerak kira -kira dalam 3 tujuan rata -rata yaitu 35 gol, dan sebagaimana dicatat, itu adalah ukuran yang jauh lebih tepat daripada kisarannya.

Dapat melayani Anda: hiperbola

Perbedaan

Deviasi rata -rata adalah ukuran variabilitas yang jauh lebih tipis daripada kisaran, tetapi sebagaimana dihitung melalui nilai absolut dari perbedaan antara masing -masing data dan rata -rata, tidak menawarkan keserbagunaan yang lebih besar dari sudut pandang aljabar.

Oleh karena itu, varians lebih disukai, yang sesuai dengan rata -rata perbedaan kuadratik setiap data dengan rata -rata dan dihitung menggunakan rumus:

Dalam ungkapan ini, s2 menunjukkan varians, dan seperti biasa xyo mewakili masing -masing data, x̄ adalah rata -rata dan n total data.

Saat bekerja dengan sampel daripada populasi, lebih disukai untuk menghitung varians seperti ini:

Perbedaan dengan formula sebelumnya adalah bahwa dalam penyebut ada n - 1 bukan n. Kebetulan dengan membagi dengan N, varian sampel meremehkan varian populasi dari mana itu diekstraksi, tetapi tidak ketika dibagi dengan n - 1. Dalam beberapa teks ekspresi itu muncul dengan nama quasi-variza.

Dalam kasus apa pun, varians ditandai dengan selalu menjadi jumlah yang positif, tetapi menjadi rata -rata perbedaan kuadratik, penting untuk mengamati bahwa ia tidak memiliki unit yang sama dengan data dari data.

Contoh varian

Untuk menghitung varian data dari contoh kisaran dan deviasi rata -rata, nilai yang sesuai diganti dan jumlah yang ditunjukkan. Dalam hal ini dipilih untuk membagi antara N-1:

= 13.86

Deviasi standar

Varians tidak memiliki unit yang sama dengan variabel yang diteliti, misalnya, jika data datang dalam meter, varians menghasilkan meter persegi. Atau dalam contoh tujuan itu akan berada dalam tujuan kuadrat, yang tidak masuk akal.

Dapat melayani Anda: apa elemen perumpamaan? (Bagian)

Oleh karena itu, standar deviasi didefinisikan, juga disebut deviasi khas, Seperti akar kuadrat dari varian:

S = √s2

Dengan cara ini ukuran variabilitas data diperoleh dalam unit yang sama dengan ini, dan semakin rendah nilai S, semakin dikelompokkan data di sekitar rata -rata.

Baik varians dan standar deviasi adalah ukuran variabilitas yang akan dipilih ketika rata -rata aritmatika adalah ukuran kecenderungan sentral yang paling menggambarkan perilaku data.

Dan standar deviasi memiliki properti penting, yang dikenal sebagai Teorema Chebyshev: setidaknya 75% dari pengamatan berada dalam interval yang ditentukan oleh X ± 2s. Dengan kata lain, 75% dari data, paling banyak, pada jarak yang sama dengan 2s di sekitar rata -rata.

Demikian juga, setidaknya 89% dari nilai berada pada jarak 3s dari rata -rata, persentase yang dapat diperluas, asalkan banyak data tersedia dan ini mengikuti distribusi normal.

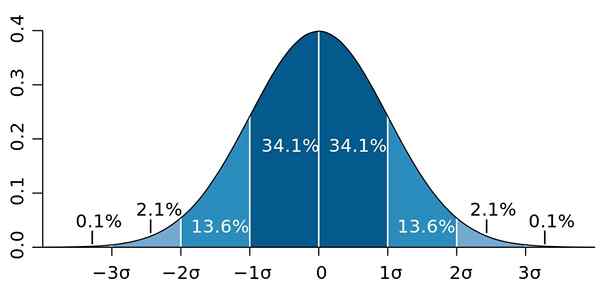
Gambar 2.- Jika data mengikuti distribusi normal, 95.4 dari mereka adalah dua standar deviasi di kedua sisi rata -rata. Sumber: Wikimedia Commons.

Contoh standar deviasi

Deviasi standar data yang disajikan dalam contoh sebelumnya adalah:

S = √s2 = √13.86 = 3.7 ≈ 4 gol