Rumus distribusi hipergeometrik, persamaan, model

Itu distribusi hipergeometrik Ini adalah fungsi statistik yang bijaksana, memadai untuk menghitung probabilitas dalam percobaan acak dengan dua hasil yang mungkin terjadi. Kondisi yang diperlukan untuk menerapkannya adalah bahwa populasi kecil, di mana ekstraksi tidak diganti dan probabilitasnya tidak konstan. 

Oleh karena itu, ketika unsur populasi dipilih untuk mengetahui hasilnya (benar atau salah) dari karakteristik tertentu, elemen yang sama tidak dapat dipilih lagi.

Gambar 1. Dalam populasi sekrup seperti ini, pasti ada spesimen yang rusak. Sumber: Pixabay.

Tentu saja, elemen berikutnya yang dipilih dengan demikian lebih mungkin untuk mendapatkan hasil yang benar, jika elemen sebelumnya memiliki hasil negatif. Ini berarti bahwa probabilitasnya bervariasi, sejauh elemen -elemen sampel diekstraksi.

Aplikasi utama distribusi hipergeometrik adalah: kontrol kualitas dalam proses dengan sedikit populasi dan perhitungan probabilitas dalam permainan acak.

Adapun fungsi matematika yang mendefinisikan distribusi hipergeometrik, ini terdiri dari tiga parameter, yaitu:

- Jumlah elemen populasi (n)

- Ukuran sampel (m) 

- Jumlah peristiwa dalam populasi lengkap dengan hasil yang menguntungkan (atau tidak menguntungkan) dari karakteristik yang diteliti (n).

[TOC]

Rumus dan Persamaan

Formula distribusi hipergeometrik memberikan probabilitas P tentang apa X kasus yang menguntungkan dari karakteristik tertentu terjadi. Cara menulisnya secara matematis, tergantung pada angka kombinatorial adalah:

Di ekspresi sebelumnya N, N Dan M Mereka adalah parameter dan X variabel itu sendiri. 

-Total populasi adalah N.

-Jumlah hasil positif dari karakteristik biner tertentu sehubungan dengan total populasi N.

-Jumlah elemen sampel M.

Pada kasus ini, X Ini adalah variabel acak yang mengambil nilai X Dan P (x) menunjukkan kemungkinan terjadinya X Kasus -kasus karakteristik yang menguntungkan yang dipelajari.

Variabel statistik penting

Variabel statistik lainnya untuk distribusi hipergeometrik adalah:

- Setengah μ = m*n/n

- Perbedaan σ^2 = m*(n/n)*(1-n/n)*(n-m)/(n-1)

- Deviasi khas σ yang merupakan akar kuadrat dari varian.

Model dan Properti 

Untuk sampai ke model distribusi hipergeometrik, ini didasarkan pada probabilitas mendapatkan X Kasus yang menguntungkan dalam sampel ukuran M. Sampel ini berisi elemen yang memenuhi properti yang diteliti dan elemen yang tidak.

Mari kita ingat itu N mewakili jumlah kasus yang menguntungkan dalam total populasi N item. Maka probabilitas akan dihitung seperti ini:

Dapat melayani Anda: ruang vektor: basis dan dimensi, aksioma, properti

P (x) = (# cara untuk mendapatkan x# dengan cara yang gagal)/(# Total cara memilih)

Mengekspresikan di atas dalam bentuk angka kombinatorial, model distribusi probabilitas berikut tercapai:

Sifat utama distribusi hipergeometrik

Adalah sebagai berikut:

- Sampel harus selalu kecil, meskipun populasinya besar.

- Unsur -unsur sampel diekstraksi dari satu, tanpa memasukkannya ke dalam populasi.

- Properti yang akan dipelajari adalah biner, yaitu hanya dapat mengambil dua nilai: 1 salah satu 0, O baik BENAR salah satu palsu.

Pada setiap langkah ekstraksi langkah, probabilitas berubah tergantung pada hasil sebelumnya.

Pendekatan dengan distribusi binomial

Properti lain dari distribusi hipergeometrik adalah dapat didekati dengan distribusi binomial, dilambangkan sebagai Dua, Selama populasinya N menjadi besar dan setidaknya 10 kali lebih besar dari sampel M. Dalam hal ini akan seperti ini:

P (n, n, m; x) = bi (m, n/n, x)           

Selama n besar dan n> 10m

Contoh

Contoh 1

Misalkan mesin yang menghasilkan sekrup dan akumulasi data menunjukkan bahwa 1% keluar dengan cacat. Kemudian dalam kotak n = 500 sekrup jumlah cacat akan:

N = 500 * 1/100 = 5

Probabilitas melalui distribusi hipergeometrik

Misalkan dari kotak itu (yaitu, dari populasi itu) kami mengambil sampel m = 60 sekrup.

Probabilitas bahwa tidak ada sekrup (x = 0) dari sampel daun yang rusak adalah 52,63%. Hasil ini tercapai saat menggunakan fungsi distribusi hipergeometrik:

P (500, 5, 60; 0) = 0,5263

Probabilitas bahwa x = 3 sekrup sampel yang rusak adalah: P (500, 5, 60; 3) = 0,0129.

Di sisi lain, probabilitas bahwa x = 4 sekrup dari enam puluhan sampel meninggalkan kerusakan adalah: P (500, 5, 60; 4) = 0,0008.

Akhirnya, probabilitas bahwa x = 5 sekrup dalam sampel itu keluar dengan cacat adalah: P (500, 5, 60; 5) = 0.

Tetapi jika Anda ingin mengetahui probabilitas bahwa dalam sampel itu ada lebih dari 3 sekrup yang rusak, maka probabilitas yang terakumulasi harus diperoleh, menambahkan:

P (3)+p (4)+p (5) = 0,0129+0,0008+0 = 0,0137.

Contoh ini diilustrasikan pada Gambar 2, diperoleh melalui penggunaan Geogebra Gunakan Perangkat Lunak Gratis Di Sekolah, Institut, dan Universitas yang Luas.

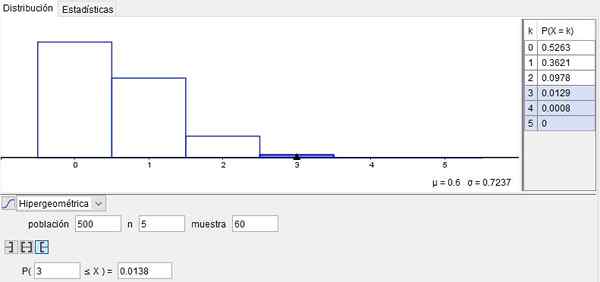Gambar 2. Contoh distribusi hipergeometrik. Disiapkan oleh f. Zapata dengan Geogebra.

Contoh 2

Dek Dek Spanyol memiliki 40 kartu, di mana 10 memiliki emas dan 30 sisanya tidak memilikinya. Misalkan 7 kartu diekstraksi dari dek itu, yang tidak kembali ke geladak.

Dapat melayani Anda: Simetri Tengah: Properti, Contoh dan Latihan

Jika x adalah jumlah emas yang ada dalam 7 kartu yang diekstraksi, maka probabilitas yang merupakan x oros dalam ekstraksi 7 kartu diberikan oleh distribusi hipergeometrik p (40,10,7; x).

Mari kita lihat ini: Untuk menghitung probabilitas memiliki 4 emas dalam ekstraksi 7 kartu, kami menggunakan rumus distribusi hipergeometrik dengan nilai -nilai berikut:

Dan hasilnya adalah: probabilitas 4,57%.

Tetapi jika Anda ingin mengetahui probabilitas mendapatkan lebih dari 4 kartu, maka kami harus menambahkan:

P (4)+p (5)+p (6)+p (7) = 5,20%

Latihan terpecahkan

Serangkaian latihan berikut dimaksudkan untuk menggambarkan dan mengasimilasi konsep yang telah disajikan dalam artikel ini. Penting bagi pembaca mencoba menyelesaikannya sendiri, sebelum melihat solusinya.

Latihan 1

Pabrik profilaksis telah menemukan bahwa dari setiap 1000 kondom yang diproduksi oleh mesin tertentu, 5 rusak. Untuk melakukan kontrol kualitas, 100 kondom diambil secara acak dan lot ditolak jika ada setidaknya satu atau lebih yang rusak. Membalas:

a) Kemungkinan apa yang harus dibuang 100 lot?

b) Apakah kriteria kontrol kualitas ini efisien?

Larutan

Dalam hal ini nomor kombinatorial yang sangat besar akan muncul. Perhitungannya sulit, kecuali paket komputer yang memadai tersedia.

Tetapi karena itu adalah populasi yang besar dan sampelnya sepuluh kali lebih sedikit dari total populasi, Anda dapat menggunakan pendekatan untuk distribusi hipergeometrik karena distribusi binomial:

P (1000,5,100; x) = bi (100, 5/1000, x) = bi (100, 0.005, x) = C (100, x)*0.005^x (1-0.005)^(100-x)

Di ekspresi sebelumnya C (100, x) Itu adalah nomor kombinatorial. Maka probabilitas Haya lebih dari satu yang rusak akan dihitung sebagai berikut:

P (x> = 1) = 1 - bi (0) = 1-.6058 = 0.3942

Ini adalah pendekatan yang sangat baik, jika dibandingkan dengan nilai yang diperoleh saat menerapkan distribusi hipergeometrik: 0.4102

Dapat dikatakan bahwa, probabilitas 40% banyak 100 profilaksis harus dibuang, yang tidak terlalu efisien.

Tapi, menjadi sedikit kurang menuntut dalam proses kontrol kualitas dan buang.

Latihan 2

Mesin taco plastik bekerja sedemikian rupa sehingga dari setiap 10 buah, seseorang cacat. Dalam sampel 5 -piece yang kemungkinan harus menjadi salah satu bagian yang rusak.

Larutan

Populasi: n = 10

Dapat melayani Anda: identitas Pythagoras: demonstrasi, contoh, latihan

Angka n cacat untuk setiap n: n = 1

Ukuran sampel: m = 5

P (10, 1, 5; 1) = c (1.1)*c (9.4)/c (10.5) = 1*126/22 = 0.5

Oleh karena itu ada probabilitas 50% bahwa dalam sampel 5, taco keluar cacat.

Latihan 3

Dalam pertemuan sekolah menengah muda ada 7 wanita dan 6 pria. Di antara gadis -gadis itu, 4 mempelajari humaniora dan 3 sains. Dalam kelompok anak laki -laki, 1 mempelajari humaniora dan 5 sains. Hitung yang berikut:

a) Memilih tiga gadis secara acak: Berapa probabilitas bahwa semua mempelajari humaniora?.

b) Jika tiga peserta dipilih secara acak untuk pertemuan teman -teman: apa yang bertiga, terlepas dari seks, pelajari ketiganya, atau humaniora juga ketiganya juga?.

c) Sekarang pilih dua teman acak dan telepon X ke variabel acak "jumlah mereka yang mempelajari humaniora". Di antara keduanya yang dipilih, tentukan nilai rata -rata atau yang diharapkan X dan varians σ^2.

Solusi untuk 

Populasinya adalah jumlah total anak perempuan: n = 7. Mereka yang mempelajari humaniora adalah n = 4, dari total. Sampel acak anak perempuan akan m = 3.

Dalam hal ini, probabilitas bahwa ketiganya adalah humaniora diberikan oleh fungsi hipergeometrik:

P (n = 7, n = 4, m = 3, x = 3) = c (4, 3) c (3, 0) / c (7, 3) = 0.1143

Lalu ada 11.Probabilitas 4% bahwa tiga chicas acak mempelajari humaniora.

Solusi b

Nilai yang akan digunakan adalah:

-Populasi: n = 14

-Kuantitas yang mempelajari huruf adalah: n = 6 dan

-Ukuran Sampel: M = 3.

-Jumlah teman yang mempelajari humaniora: x

Menurut ini, x = 3 berarti bahwa tiga studi humaniora, tetapi x = 0 berarti tidak ada yang mempelajari humaniora. Probabilitas bahwa tiga studi yang sama diberikan oleh jumlah:

P (14, 6, 3, x = 0) + p (14, 6, 3, x = 3) = 0.0560 + 0.1539 = 0.2099

Kemudian, kami memiliki probabilitas 21% bahwa tiga peserta pertemuan, dipilih secara acak, mempelajari hal yang sama.

Solusi c

Di sini kita memiliki nilai -nilai berikut:

N = 14 total populasi teman, n = 6 jumlah total dalam populasi yang mempelajari humaniora, ukuran sampel adalah m = 2.

Harapannya adalah:

E (x) = m * (n/n) = 2 * (6/14) = 0.8572

Dan variannya:

σ (x)^2 =  m*(n/n)*(1-n/n)*(n-m)/(n-1) = 2*(6/14)*(1-6/14)*(14-2)/(14 -1) =

= 2*(6/14)*(1-6/14)*(14-2)/(14-1) = 2*(3/7)*(1-3/7)*(12) (13)  = 0.4521

Referensi

1. Distribusi probabilitas diskrit. Pulih dari: biploot.usal.adalah
2. Statistik dan probabilitas. Distribusi hipergeometrik. Diperoleh dari: Projectescartes.org
3. CDPYE-UGR. Distribusi hipergeometrik. Dipulihkan dari: UGR.adalah
4. Geogebra. Geogebra klasik, perhitungan probabilitas. Pulih dari Geogebra.org
5. Probate yang mudah. Latihan distribusi hipergeometrik terpecahkan. Pulih dari: probafacil.com
6. Minitab. Distribusi hipergeometrik. Diperoleh dari: Dukungan.Minitab.com
7. Universitas Vigo. Distribusi diskrit utama. Pulih dari: anapg.situs web.Uvigo.adalah
8. Vitutor. Statistik dan kombinatorial. Diperoleh dari: Vitutor.bersih
9. Weisstein, Eric W. Distribusi hipergeometrik. Dipulihkan dari: MathWorld.Wolfram.com
10. Wikipedia. Distribusi hipergeometrik. Pulih dari: is.Wikipedia.com