Konsep eksperimen acak, ruang sampel, contoh

Ada pembicaraan Eksperimen acak Ketika hasil dari setiap percobaan tertentu tidak dapat diprediksi, bahkan ketika probabilitas terjadinya hasil tertentu dapat ditetapkan.

Namun, harus diklarifikasi bahwa tidak mungkin untuk mereproduksi hasil yang sama dari sistem acak dengan parameter dan kondisi awal yang sama dalam setiap percobaan percobaan.

Gambar 1. Peluncuran DICE adalah percobaan acak. Sumber: Pixabay.

Contoh yang baik dari percobaan acak adalah peluncuran dadu. Bahkan ketika Anda berhati -hati untuk meluncurkan dadu dengan cara yang sama, dalam setiap upaya hasil yang tidak dapat diprediksi akan diperoleh. Sebenarnya, satu -satunya hal yang dapat ditegaskan adalah bahwa hasilnya bisa menjadi beberapa hal berikut: 1, 2, 3, 4, 5 atau 6.

Peluncuran mata uang adalah contoh lain dari percobaan acak dengan hanya dua hasil yang mungkin: wajah atau segel. Meskipun mata uang diluncurkan dari ketinggian yang sama dan dengan cara yang sama, faktor peluang akan selalu ada, yang menghasilkan ketidakpastian untuk setiap upaya baru.

Kebalikan dari percobaan acak adalah percobaan deterministik. Misalnya, diketahui bahwa setiap kali air direbus pada permukaan laut suhu mendidih adalah 100 ºC. Tetapi tidak pernah terjadi bahwa, mempertahankan kondisi yang sama, hasilnya terkadang 90 ºC, 12 0ºC lainnya dan kadang -kadang 100 ºC.

[TOC]

Ruang sampel

Set semua hasil yang mungkin dari percobaan acak disebut ruang sampel. Dalam percobaan acak peluncuran dadu, ruang sampel adalah:

D = 1, 2, 3, 4, 5, 6.

Untuk bagiannya, pada peluncuran mata uang ruang sampel adalah:

M = face, seal.

Acara atau acara

Dalam percobaan acak, a peristiwa Itu adalah kejadian atau tidak dari hasil tertentu. Misalnya, dalam hal peluncuran mata uang, suatu acara atau acara menjadi mahal.

Dapat melayani Anda: sisi homolog

Peristiwa lain dalam percobaan acak bisa sebagai berikut: bahwa pada peluncuran dadu angka kurang dari tiga dirilis.

Jika acara berlangsung, maka himpunan hasil yang mungkin adalah set:

E = 1, 2, 3

Pada gilirannya, ini adalah subset dari ruang atau set sampel:

M = 1, 2, 3, 4, 5, 6.

Contoh

Di bawah ini adalah beberapa contoh yang menggambarkan hal di atas:

Contoh 1

Asumsikan bahwa dua koin dilemparkan, satu demi satu. Itu diminta:

a) menunjukkan apakah itu percobaan acak atau sebaliknya percobaan deterministik.

b) Berapa ruang sampel dari percobaan ini?

c) Tunjukkan seluruh peristiwa A, sesuai dengan percobaan memiliki hasil wajah dan perangko.

d) Hitung probabilitas bahwa peristiwa tersebut terjadi.

e) Akhirnya, temukan probabilitas bahwa peristiwa B: tidak tampak menghadapi hasilnya.

Larutan 

a) Ini adalah percobaan acak karena tidak ada cara untuk memprediksi apa yang akan menjadi hasil dari peluncuran kedua koin.

b) Ruang sampel adalah himpunan semua hasil yang mungkin:

S = (c, c), (c, s), (s, c), (s, s)

c) Acara A, dalam kasus yang diberikan, dapat memiliki hasil berikut:

A = (c, s), (s, c)

d) Probabilitas Acara A diperoleh dari membagi jumlah elemen dari himpunan A antara jumlah elemen dari set yang sesuai dengan ruang sampel:

P (a) = 2/4 = ½ = 0.5 = 50%

e) Hasil hasil yang mungkin sesuai dengan peristiwa B (tidak muncul wajah pada hasilnya) adalah:

Dapat melayani Anda: trinomial persegi yang sempurna

B = (s, s)

Jadi probabilitas bahwa peristiwa B terjadi dalam esai adalah rasio antara jumlah kemungkinan hasil B antara jumlah total kasus:

P (b) = ¼ = 0.25 = 25%.

Contoh 2

Tas berisi 10 kelereng putih dan 10 kelereng hitam. Dari tas mereka dilepas secara acak dan tanpa melihat ke dalam tiga kelereng berturut -turut. 

a) Tentukan ruang sampel dari percobaan acak ini.

b) Tentukan himpunan hasil yang sesuai dengan peristiwa yang setelah percobaan ada dua kelereng hitam.

c) Event B adalah untuk mendapatkan setidaknya dua kelereng hitam, tentukan set B hasil untuk acara ini.

d) Berapa probabilitas acara tersebut terjadi?

e) Temukan probabilitas peristiwa itu b.

f) Tentukan probabilitas bahwa hasil dari percobaan acak adalah bahwa setidaknya satu marmer hitam. Acara ini akan disebut C.

Gambar 2. Kelereng hitam dan hitam untuk percobaan acak. Sumber: Needpix.

Solusi untuk

Untuk membangun ruang sampel, penting untuk membuat diagram pohon, seperti yang ditunjukkan pada Gambar 3:

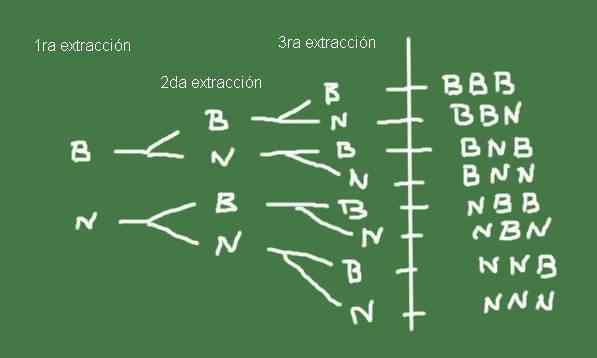Gambar 3. Diagram pohon misalnya 2. Disiapkan oleh fanny zapata.

Hasil Ω yang mungkin terjadi dari mengekstraksi tiga kelereng dari tas dengan jumlah kelereng hitam dan hitam yang sama, justru ruang sampel dari percobaan acak ini.

Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)

Solusi b

Hasil hasil yang mungkin sesuai dengan Acara A, yang terdiri dari memiliki dua kelereng hitam adalah:

Dapat melayani Anda: Jumlah Riemann: Sejarah, Rumus dan Properti, Latihan

A = (b, n, n), (n, b, n), (n, n, b)

Solusi c

Event B didefinisikan sebagai: "untuk memiliki setidaknya dua kelereng hitam setelah membuat ekstraksi acak dari mereka". Hasil hasil yang mungkin untuk Event B adalah:

B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)

Solusi d

Probabilitas memiliki peristiwa A adalah rasio antara jumlah hasil yang mungkin untuk peristiwa ini, dan jumlah total hasil yang mungkin, yaitu, jumlah elemen ruang sampel.

P (a) = n (a) / n (Ω) = 3/8 = 0.375 = 37.5%

Jadi ada 37.Probabilitas 5% memiliki dua kelereng hitam setelah diekstraksi secara acak tiga kelereng dari tas. Tetapi perhatikan bahwa kita sama sekali tidak dapat memprediksi hasil yang tepat dari percobaan.

Solusi e

Probabilitas bahwa peristiwa B diberikan, terdiri dari setidaknya satu marmer hitam adalah:

P (b) = n (b) / n (Ω) = 4/8 = 0.5 = 50%

Ini berarti bahwa kemungkinan peristiwa B sama dengan probabilitas yang tidak terjadi. 

Solusi f

Probabilitas mendapatkan setidaknya satu marmer hitam, setelah mengekstraksi tiga dari mereka, sama dengan 1 lebih sedikit probabilitas bahwa hasilnya adalah "tiga kelereng putih".

P (c) = 1 - p (b b b) = 1 - ⅛ = ⅞ = 0.875 = 87.5%

Sekarang, kami dapat memverifikasi hasil ini, mencatat bahwa jumlah kemungkinan yang diberikan peristiwa C sama dengan jumlah elemen dari hasil yang mungkin untuk acara C:

C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, n, b) , (n, n, n)

N (c) = 7

P (c) = n (c) / n (Ω) = ⅞ = 87.5%

Referensi

1. Canalphi. Eksperimen acak. Dipulihkan dari: YouTube.com.
2. Mathemovil. Eksperimen acak. Dipulihkan dari: YouTube.com
3. Pishro nick h . Pengantar probabilitas. Diperoleh dari: ProbabilityCourse.com
4. Ross. Probabilitas dan Statistik untuk Insinyur. MC-Graw Hill.
5. Wikipedia. Eksperimen (teori probabilitas). Diperoleh dari: di.Wikipedia.com
6. Wikipedia. Peristiwa deterministik. Pulih dari: is. Wikipedia.com
7. Wikipedia. Eksperimen acak. Pulih dari: is.Wikipedia.com