120 Pembagi

Itu 120 Pembagi Mereka semua adalah angka -angka yang membaginya dengan tepat. Angka -angka ini adalah sebagai berikut:

Pembagi 120 = 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 30, 40, 60, 120

Juga lawan dari rangkaian angka ini, yaitu, negatif, adalah 120 pembagi, karena divisi ini tepat. 120 memiliki 16 pembagi seluruh positif dan banyak negatif lainnya.

Ada beberapa cara untuk menemukan pembagi angka. Jika ini tidak terlalu besar, Anda dapat menggunakan tabel multiplikasi (untuk angka kurang dari 100) dan verifikasi di mana tabel nomor yang dimaksud muncul. Sebagai contoh, 12 muncul di tabel 2, 3, 4 dan 6, dan ini adalah pembagi mereka, bersama dengan 1 dan 12 yang sama.

Jumlahnya juga dapat dipecah menjadi faktor utamanya, menerapkan aturan pembagian dan melipatgandakan faktor -faktor tersebut. Tetapi Anda harus berhati -hati untuk tidak melewati pembagi yang diabaikan.

Karena 120 lebih besar dari 100, tidak secara langsung dalam tabel multiplikasi, namun, tidak terlalu melelahkan untuk menemukan 16. Prosedur yang valid untuk semua angka ditampilkan segera, melalui penggunaan tabel yang sangat sederhana.

Berapa banyak pembagi 120?

Pertama, jumlah pembagi 120 ditemukan. Ada formula yang memungkinkan Anda untuk mengetahui berapa banyak yang Anda miliki, meskipun tidak mengatakan apa adanya.

Angka gabungan, seperti 120, dapat dinyatakan sebagai produk bilangan prima, atau kekuatan ini. Memanggil n ke nomor senyawa apa pun:

N = a^N ∙ b^M ∙ c^P … R^k

Dapat melayani Anda: Hubungan Proporsionalitas: Konsep, Contoh dan Latihan

Angka A, B, C ... R adalah bilangan prima, dan nilai N, M, P, ... K, kekuatan masing -masing. Dekomposisi dalam faktor utama 120 adalah sebagai berikut:

120 | 2
60 | 2
30 | 2
15 | 3
5 | 5
1 | 1

Dengan cara ini, 120 adalah produk dari faktor -faktor tersebut:

120 = 2³ ∙ 3 ∙ 5

Formula untuk menghitung jumlah pembagi n

Jumlah pembagi = (n +1) × (m +1) × (p +1) ... × (k +1)

Sekarang rumus hingga 120 diterapkan. Dari dekomposisi dalam faktor -faktor yang harus Anda lakukan:

n = 3 (adalah kekuatan 2)

M = 1 (3 meningkat menjadi 1: 3¹ = 3)

P = 1 (5 juga muncul meningkat menjadi 1)

Dengan nilai -nilai ini:

Jumlah pembagi 120 = (3 +1) × (1 +1) × (1 +1) = 4 × 2 × 2 = 16

Hasil ini bertepatan dengan awal awal: 120 memiliki 16 pembagi. Selain itu, sudah diketahui bahwa 2, 3 dan 5 adalah pembagi 120, serta 10, karena angka apa pun yang selesai dalam 0 dapat dibagi dengan 10. Prosedur untuk menemukan semuanya segera ditampilkan.

Perhitungan pembagi 120

Itu dilakukan dengan bantuan faktor -faktor yang dihitung di bagian sebelumnya. Di sana terlihat bahwa 2 adalah faktor utama dengan eksponen 3, dan 3 adalah faktor sepupu lain, dengan eksponen 1. Dengan informasi ini, tabel berikut ini dibangun:

Perhatikan bahwa kekuatan 2 dimulai dalam 2⁰ dan berakhir dengan 2³, yang merupakan faktor yang muncul saat membusuk 120. Ingat itu 2⁰ dan 3⁰ Keduanya sama dengan 1 (angka apa pun yang tinggi ke 0 adalah 1). Untuk Faktor 3, dimulai dalam 3⁰ Sampai 3¹, sejak 3¹ = 3.

Selanjutnya, tabel diselesaikan dengan produk angka berbaju merah, seperti yang ditunjukkan di sini:

Dapat melayani Anda: invers multiplikasi: penjelasan, contoh, latihan terpecahkan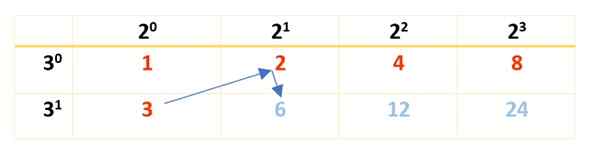

Semua angka merah dan biru adalah 120 pembagi, tetapi hampir tidak ada 8. Untuk menemukan yang tersisa, tabel baru meledak, para pembagi yang sudah diperoleh di barisan depan dan faktor yang masih harus diperhitungkan ditulis: 5, dengan kekuatan mereka di kolom pertama, di sebelah kiri, seperti ini:

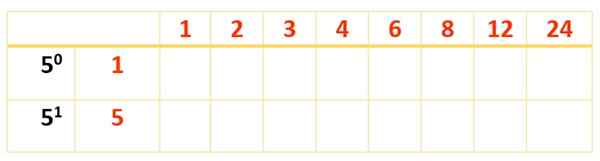
Sekarang, tabel diselesaikan dengan produk -produk angka merah, seperti yang dilakukan dengan tabel pertama:

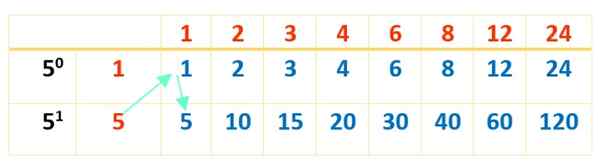
Dan akhirnya 16 pembagi 120 dengan warna biru muncul. Tabel adalah bantuan yang sangat baik untuk operasi yang harus dilakukan secara berurutan dan dengan demikian tidak ada pembagi 120.

Latihan terpecahkan

Prosedur untuk menemukan semua pembagi dari angka dirangkum sebagai berikut:

1. Memecah angka menjadi faktor utama.
2. Hitung jumlah pembagi dengan formula.
3. Bangun tabel yang diperlukan untuk menemukan pembagi. Jika jumlahnya memiliki dua faktor, sebuah tabel sudah cukup, jika Anda memiliki tiga faktor, dua tabel harus dibuat, seperti dalam kasus 120.

Latihan 1

Temukan semua pembagi dari 288.

Larutan

288 terurai menjadi faktor utama:

288 | 2
144 | 2
72 | 2
36 | 2
18 | 2
9 | 3
3 | 3
1 | 1

288 ditulis seperti ini:

288 = 2⁵ ∙ 3²

Segera adalah jumlah pembagi dari 288 hingga:

Jumlah pembagi = (n +1) × (m +1) × (p +1) ... × (k +1)

Dari dekomposisi dalam faktor utama dicatat bahwa n = 5 dan m = 2, lalu:

Pembagi 288 = (5 +1) × (2 +1) = 6 × 3 = 18

Ada 18 pembagi dan karena hanya ada dua faktor, itu cukup dengan hanya satu tabel:

Dapat melayani Anda: karakteristik persegi panjang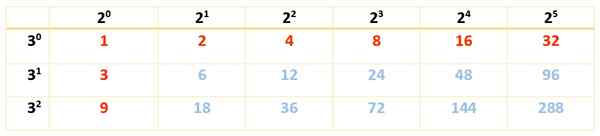

Pembagi 288 adalah angka berwarna merah dan biru:

Div (288) = 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288

Mereka dapat diperiksa dengan cepat dengan bantuan kalkulator.

Latihan 2

Temukan pembagi 350

Larutan

350 terurai:

350 | 2
175 | 5
35 | 5
7 | 7
1 | 1

350 dapat ditulis sebagai produk dari tiga faktor:

350 = 2 ∙ 5²∙ 7

Langkah selanjutnya adalah menghitung berapa banyak pembagi yang dimiliki, melalui rumus:

Jumlah pembagi = (n +1) × (m +1) × (p +1) ... × (k +1)

Dengan n = 1, m = 2, p = 1

Pembagi 288 = (1 +1) × (2 +1) × (1 +1) = 2 × 3 × 2 = 12

Karena 350 membutuhkan tiga faktor, dua tabel harus dibuat. Yang pertama dilakukan dengan 2 dan 5², Tetapi juga bisa dilakukan dengan 2 dan 7, atau dengan 7 dan 5², Menurut preferensi, karena dalam semua bentuk, hasil akhirnya sama:

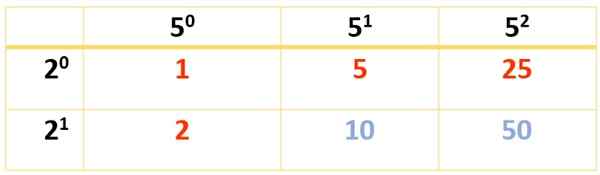
6 pembagi diperoleh. Yang lain muncul dengan bantuan tabel lain ini:

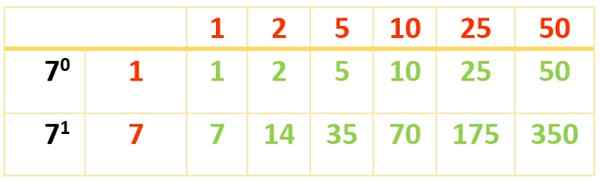
Pembagi 350 adalah:

Div (350) = 1, 2, 5, 7, 10, 14, 25, 35, 50, 70, 175, 350