Persamaan clausius-clapeyron untuk apa, contoh, latihan
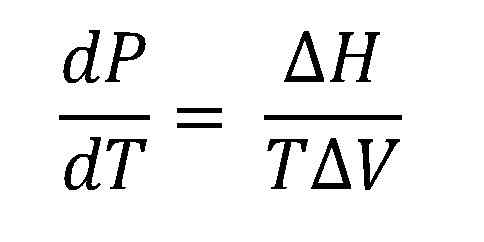
- 4820
- 965
- Domingo Gutkowski
Itu Persamaan Clausius-Clapeyron Ini adalah salah satu yang menghubungkan perubahan tekanan uap dan suhu, dalam fase atau perubahan transisi keadaan. Berlaku untuk sublimasi, evaporasi, merger, atau bahkan perubahan dalam fase kristal. Perlu disebutkan bahwa persamaan ini berlaku untuk zat murni yang ada dalam keseimbangan.
Persamaan ini berasal dari hukum termodinamika dan diagram P-T untuk suatu zat, di mana garis koeksistensi diamati; Apa yang memisahkan dua fase berbeda (uap cair, padat-cair, dll.). Untuk mentransfer jalur ini, gain atau kehilangan panas diperlukan, seperti entalpi penguapan, ΔHUap.
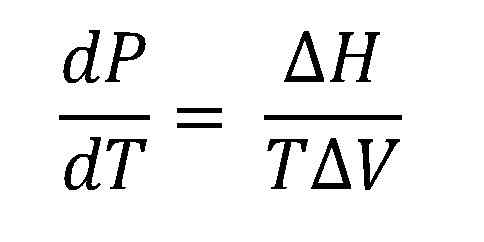 Persamaan Clausius-Clapeyron. Sumber: Gabriel Bolívar.
Persamaan Clausius-Clapeyron. Sumber: Gabriel Bolívar. Gambar yang lebih tinggi menunjukkan persamaan Clausius-Clapeyron sebelum diintegrasikan. Biasanya biasanya diterapkan pada sistem uap cair, di mana ΔH digunakanUap dan Anda ingin menghitung apa tekanan uap cair pada suhu tertentu. Itu juga berfungsi untuk menghitung ΔHUap cairan tertentu dalam kisaran suhu.
Persamaan Clausisu-Clapeyron juga cukup sering digunakan untuk mempelajari perubahan tekanan pada padatan yang mudah menguap; yaitu entalpi sublimasi dipertimbangkan, ΔHsub.
[TOC]
Untuk apa persamaan Clausisu-Clapeyron?
Perhitungan tekanan tekanan dan entalpi penguapan
Dari persamaan Clausius-Clapeyron dari atas, beberapa pertimbangan matematika akhirnya dibuat untuk akhirnya melakukan integrasi. Misalnya, untuk sistem uap cair, diasumsikan bahwa ΔHUap Itu tidak berbeda dengan suhu, dan ΔV sesuai secara eksklusif dengan volume uap, membenci volume cairan (vuap-Vcairan = Vuap).
Dengan asumsi bahwa uap berperilaku sebagai gas yang ideal dan mengintegrasikan, persamaan Clausius-Clapeyron terintegrasi diperoleh:
Dapat melayani Anda: volatilisasi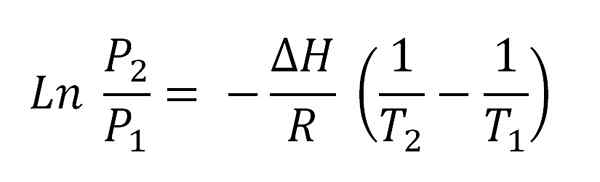 Persamaan Clausius-Clapeyron terintegrasi.
Persamaan Clausius-Clapeyron terintegrasi. Persamaan ini sesuai dengan garis yang grafis sebagai:
Ln p vs 1/t
Dan kemiringan negatifnya (ΔH/r). Untuk memenuhi persamaan ini, oleh karena itu, ΔH harus konstan dalam interval suhu (t2-T1) di mana tekanan uap diukur dalam kesetimbangan dengan cairan.
Dengan cara ini, jika diasumsikan bahwa ΔH bervariasi sedikit dalam interval suhu kecil, dimungkinkan untuk menggunakan persamaan garis ini untuk memprediksi perubahan tekanan uap cairan; Dan bahkan lebih lagi, Anda dapat menentukan ΔH penguapannya.
Semakin besar interval suhu yang dipertimbangkan, semakin terbesar penyimpangan persamaan data eksperimental ini, dan semakin sedikit yang akan dipenuhi.
Penentuan Perubahan Fase
Dengan demikian, persamaan Clausius-Clapeyron menjadi pengembangan garis garis singgung ke garis koeksistensi antara dua fase fisik, yang diamati dalam diagram P-T untuk suatu zat untuk suatu zat.
Jika perubahan fase terjadi, akan ada perubahan pada lereng, dan ΔH tidak akan sama. Oleh karena itu, ketika penyimpangan yang kuat dibuktikan dan persamaan gagal, itu adalah tanda bahwa dalam interval suhu zat mengalami perubahan fase lain. Artinya, itu tidak lagi menjadi sistem uap cair, karena diteruskan ke garis koeksistensi yang sesuai dengan penyeimbangan padat-cair atau uap padat.
Gunakan contoh
- Persamaan Clausius-Clapeyron telah digunakan dalam meteorologi untuk mempelajari perilaku awan, bahkan yang hadir di planet atau bulan lain dengan atmosfer.
Dapat melayani Anda: asam glukonat: struktur, sifat, sintesis, penggunaan- Ini telah digunakan dalam menentukan entalpi fusi dari beberapa logam seperti natrium dan gallium, dan untuk memperkirakan tekanan uapnya pada suhu yang sangat tinggi.
- Ini juga telah digunakan untuk menentukan entalpi penguapan zat seperti gaseous klorin, karbon tetraklorida, air cair, es dan yodium.
- Ini juga berfungsi untuk mempelajari perubahan fase dalam struktur kristal. Dalam contoh terakhir ini, persamaan terintegrasi Clausius-Clapeyron terlihat sangat berbeda, karena pertimbangan yang sama yang diambil untuk sistem uap cair tidak dapat dibuat untuk ΔV. Variasi volume dari satu fase ke fase lain kali ini kecil.
Latihan terpecahkan
- Latihan 1
Tekanan uap es adalah 4.58 torr pada 0 ° C dan 1.95 Torr A -10 ° C. Apa entalpi sublimasi Anda dalam kisaran suhu itu?
Perhatikan bahwa kami memiliki dua tekanan dan dua suhu:
P1 = 4.58 Torr
P2 = 1.95 Torr
T1 = 0 ° C + 273 = 273 K
T2 = -10 ° C + 273 = 263 K
Kami mengonversi unit suhu dari ° C ke K, karena konstan gas memiliki k dalam unitnya:
R = 8.314 j/k
Dengan demikian, kami menggunakan persamaan Clausius-Clapeyron yang terintegrasi dan jelas ΔHsub, yang akan tetap sebagai:
ΔHsub = -Rln (p2/P1) / (1 / t2 - 1 /t1)
Untuk lebih banyak kenyamanan akan melanjutkan untuk mengganti hanya dengan angka, tetapi mengetahui bahwa unit terakhir akan menjadi Joule:
ΔHsub = -(8.314) ln (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Atau 51.07 J mempertimbangkan beberapa desimal. Nilai ini akan menghadirkan osilasi tergantung pada interval t2-T1 dan tekanan uap tertentu.
- Latihan 2
Titik mendidih etanol pada tekanan 760 torr (1 atm) adalah 78.3 ° C, dan entalpi penguapannya adalah 39.3 kJ. Apa tekanan uap Anda pada suhu 46 ° C?
Itu dapat melayani Anda: tantalus: struktur, sifat, penggunaan, mendapatkanKami mengidentifikasi data:
P1 = 760 torr
P2 = ?
T1 = 78.3 ° C + 273 = 351.3 k
T2 = 46 ° C + 273 = 319 K
ΔHUap = 39.3 kJ atau 39300 j
Jadi, kita harus membersihkan P2 dari persamaan Clausius-Clapeyron yang terintegrasi. Sekali lagi, unit akan dihilangkan untuk kenyamanan dan perhitungan akan dikembangkan langkah demi langkah:
Ln (hal2/P1) = -(ΔHUap/R) (1/t2 - 1/t1)
Ln (hal2/760) = -(39300/8.314) (1/319 - 1/351.3)
Ln (hal2/760) = -1.36
Menerapkan fungsi eksponensial di kedua sisi persamaan untuk dapat menghapus p2 kami akan memiliki:
E (ln p2/760) = e(-1.36)
P2/760 = 0.256
P2 = 0.256 (760)
= 195 Torr
Pada suhu yang lebih rendah (46 ° C), tekanan uap lebih rendah (195 torr). Faktanya, memiliki tekanan etanol 760 torr menjadi 78.3 ° C, kita berbicara tentang titik didih normal. Ini adalah perilaku yang diharapkan untuk semua cairan
Secara umum, latihan Clausius-Clapeyron jenis ini terdiri dari kliring P2, T2 atau ΔH penguapan atau sublimasi. Perhitungan berubah secara signifikan ketika ΔV juga harus dipertimbangkan, terutama ketika menyangkut sistem atau keseimbangan yang cair-cair.
Referensi
- Whitten, Davis, Peck & Stanley. (2008). Kimia. (Edisi ke -8.). Pembelajaran Cengage.
- Wikipedia. (2020). Hubungan Clausius-Clapeyron. Diperoleh dari: di.Wikipedia.org
- Universitas Negeri San José. (S.F.). Persamaan Clausius-Clapeyron:
Derivasi dan aplikasi IMS dalam meteorologi. Pulih dari: sjsu.Edu - BODNER GROUP. (S.F.). Persamaan Clausius-Clapeyron. Diperoleh dari: chemed.Chem.Purdue.Edu
- Chieh c. & Censulo a. (18 Mei 2020). Persamaan Clausius-Clapeyron. Libretteks Kimia. Pulih dari: chem.Librettexts.org
- Walter J. Moore. (1962). Kimia Fisik. (Edisi keempat). Longmans.

