Persamaan Parabola Umum (contoh dan latihan)

Itu Persamaan Umum Perumpamaan Berisi istilah kuadratik di X dan masuk Dan, serta istilah linier di kedua variabel ditambah istilah independen. Sumbu simetri pertama sejajar dengan sumbu vertikal dan yang kedua adalah sumbu horizontal.

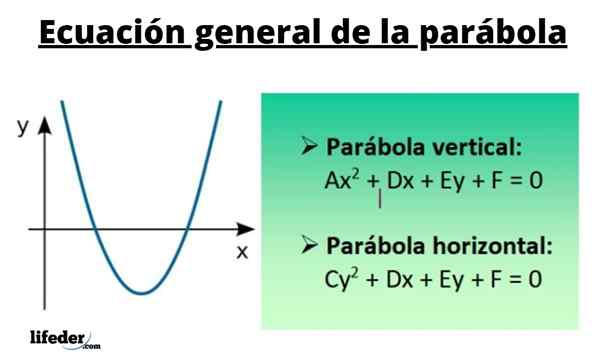
Secara umum, persamaan kuadratik yang tidak memiliki istilah silang Xy Itu ditulis sebagai:

Kapak² + Cy² +Dx + ey + f = 0

Nilai a, c, d, e dan f adalah bilangan real. Memaksakan kondisi pada ∙ c = 0 dan a+c ≠ 0, kurva yang dihasilkan dari grafik titik yang memenuhi persamaan ini adalah parabola.

Kasus 1

Untuk perumpamaan vertikal, persamaan umumnya adalah:

Kapak² + Dx + ey + f = 0

Dimana a dan e berbeda dari 0. Dengan kata lain, ketika suatu istilah muncul dengan x², Perumpamaannya vertikal.

Kasus 2

Untuk bagiannya, untuk perumpamaan horizontal yang Anda miliki:

Cy² + Dx + ey + f = 0

Di sini C dan D juga berbeda dari 0, oleh karena itu istilah kuadratik sesuai dengan dan².

Bagaimanapun, persamaan umum perumpamaan adalah kuadratik dalam salah satu variabel dan linier di yang lain.

Elemen perumpamaan

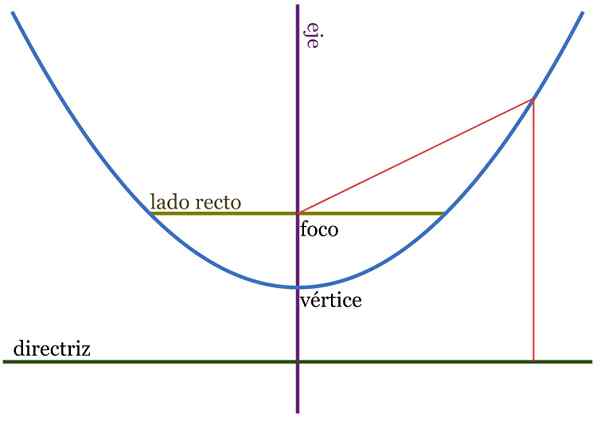Gambar 2. Elemen perumpamaan. Jarak QF dan QH sama. Sumber: Wikimedia Commons.

Parabola, didefinisikan sebagai tempat geometris, terdiri dari himpunan titik satu bidang yang menyamakan dari titik lain yang disebut fokus Dan juga garis, yang dikenal sebagai Pedoman Lurus.

Dari persamaan umum, dimungkinkan untuk mempelajari perumpamaan dengan menentukan elemen -elemennya. Termasuk fokus dan pedoman, elemen -elemen ini, yang dijelaskan secara singkat adalah:

-Sumbu, yang mengacu pada sumbu simetri parabola, dapat horizontal (sejajar dengan sumbu absis) atau vertikal (sejajar dengan sumbu ordinat).

Dapat melayani Anda: faktor umum untuk istilah pengelompokan: contoh, latihan

-Orientasi, yang pada gilirannya sesuai dengan orientasi sumbu. Perumpamaannya vertikal jika sumbu simetrinya vertikal, dan horizontal saat sumbu juga.

-Puncak, Itu adalah titik di mana sumbu memotong perumpamaan.

-Fokus, Titik terletak di atas poros, di dalam perumpamaan dan di kejauhan P dari simpul. Semua titik para Equidist parabola fokus dan arah pedoman.

-Parameter, Itu adalah jarak P Antara fokus dan titik.

-Pedoman Lurus, yang tegak lurus terhadap sumbu y dan juga jarak P dari titik perumpamaan, tetapi tidak memotongnya, karena ada di luar.

-Sisi lurus, Itu adalah tali yang melewati fokus, memotong perumpamaan dalam dua titik, tegak lurus terhadap porosnya.

-Keanehan, bahwa dalam kasus parabola selalu bernilai 1.

-Representasi Grafik.

Informasi untuk menentukan semua elemen ini terkandung dalam persamaan umum.

Bentuk kanonik

Untuk menentukan unsur -unsur parabola, kadang -kadang lebih mudah untuk meneruskan bentuk umum ke bentuk kanonik yang sama, dengan cara metode menyelesaikan kotak dalam variabel kuadratik.

Bentuk kanonik ini adalah:

(X-H)² = 4p (y-k)

Di mana titik (h, k) adalah simpul V dari perumpamaan. Bentuk kanonik untuk persamaan umum juga dapat menjadi, mengembangkan produk terkenal dan mengatur ulang persyaratan.

Contoh

Contoh 1

Berikut ini adalah persamaan parabola secara umum:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x -dan² = 0

Dalam a) koefisien diidentifikasi: a = 4, c = 0, d = 0, e = 5, f = -3. Ini adalah perumpamaan yang poros simetri yang vertikal.

Dapat melayani Anda: Divisi sintetis

Untuk bagiannya, dalam B) persamaan umum tetap:

- Dan² + 3x - 2y + 1 = 0

Dan koefisiennya adalah: c = -1, d = 3, e = -2 dan f = 1.

Contoh 2

Perumpamaan berikutnya adalah dalam bentuk kanonik:

(Y-1)² = 6 (x-3)

Untuk menemukan persamaan umumnya, produk terkenal dikembangkan dan tanda kurung dilakukan di sebelah kanan:

Dan² -2y + 1 = 6x -18

Sekarang semua istilah di sebelah kiri dilewati dan mereka dikelompokkan dengan nyaman:

Dan² -2y + 1- 6x +18 = 0 → dan² - 6x -2y + 19 = 0

Sebagai istilah kuadratik dan² Ini adalah perumpamaan horizontal. Koefisiennya adalah:

C = 1; D = -6; E = -2, f = 19.

Latihan terpecahkan

Latihan 1

Perumpamaan berikutnya diberikan secara umum:

X² -10x -12y - 11 = 0

Diminta untuk menulisnya dalam bentuk kanonik.

Larutan

Pergi ke bentuk kanonik dicapai dengan mengisi kotak, dalam hal ini, dalam variabel x. Istilah dalam X dimulai dalam tanda kurung:

(X² -10x) -12y - 11 = 0

Anda harus mengubah apa yang ada dalam tanda kurung menjadi trinomial persegi yang sempurna, yang dicapai dengan menambahkan 5², Itu secara alami harus dikurangi, karena jika tidak, ekspresi diubah. Tetap seperti ini:

(X² −10x+5²) −12y - 11−5²= 0

Tiga istilah dalam tanda kurung merupakan trinomial persegi yang sempurna (X-5)². Itu dapat diperiksa dengan mengembangkan produk terkenal ini untuk menguatkan. Sekarang perumpamaan tetap:

(X-5)² -12y -36 = 0

Berikut ini adalah memperhitungkan istilah di luar tanda kurung:

(X-5)² -12 (y +3) = 0

Yang akhirnya berubah menjadi:

(X-5)² = 12 (y +3)

Contoh 2

Temukan elemen perumpamaan sebelumnya dan bangun grafik Anda.

Larutan

Puncak

Titik parabola memiliki koordinat V (5, -3)

Itu bisa melayani Anda: prisma hepagonal

Sumbu

Garis x = 5.

Parameter

Mengenai nilai parameter P yang muncul dalam bentuk kanonik: (x-h)² = 4p (y-k) membandingkan kedua persamaan:

4p = 12

P = 12/4 = 3

Orientasi

Perumpamaan ini vertikal dan terbuka. Karena simpul terletak di x = 5, y = -3, maka sumbu simetri adalah garis vertikal x = 5.

Fokus

Fokusnya adalah pada garis x = 5, oleh karena itu ia memiliki koordinat x = 5 juga.

Koordinat Dan dari fokus harus P unit di atas k, yaitu: p + k = 3 + (-3) = 0, maka fokusnya pada titik (5.0).

Pedoman Lurus

Ini tegak lurus terhadap sumbu, oleh karena itu bentuk y = c, sekarang, karena jarak p dari titik jauh dari, tetapi di luar perumpamaan, itu berarti berada pada jarak p di bawah k:

y = k -p = -3-3 = -6

Sisi lurus

Segmen ini dipotong ke perumpamaan, melewati fokus dan sejajar dengan pedoman, oleh karena itu terkandung pada baris y = 0.

Representasi Grafik

Ini dapat dengan mudah diperoleh dari perangkat lunak grafik online gratis, seperti Geogebra. Di kotak masuk ditempatkan sebagai berikut:

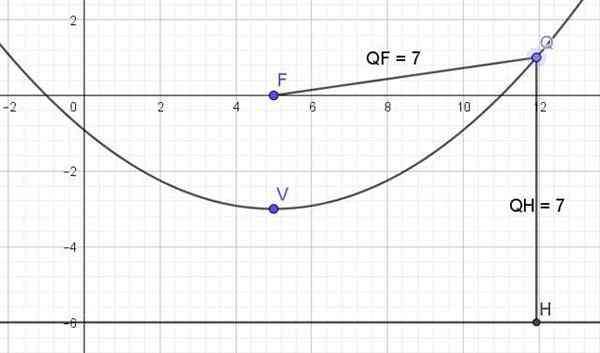Gambar 3. Grafik perumpamaan x² -10x -12y - 11 = 0. Sumber: f. Zapata.

Referensi

1. Baldor. 1977. Aljabar Dasar. Edisi Budaya Venezuela.
2. Hoffman, J. Pemilihan masalah matematika. Volume 2.
3. Jiménez, r. 2008. Aljabar. Prentice Hall.
4. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
5. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.