Gibbs Unit Energi Bebas, Bagaimana Dihitung, Latihan Diselesaikan

Itu Energi bebas Gibbs (biasa disebut g) adalah potensi termodinamika yang didefinisikan sebagai perbedaan entalpi H, kecuali produk dari suhu T, oleh entropi sistem:

G = h - t s

Gibbs Free Energy diukur dalam joule (menurut sistem internasional), dalam ergio (untuk sistem liga unit), dalam kalori atau volt elektron (Untuk elektro volt).

Gambar 1. Diagram yang menunjukkan definisi energi Gibbs dan hubungannya dengan potensi termodinamika lainnya. Sumber: Daya Nuklir.bersih.

Dalam proses yang terjadi pada tekanan dan suhu konstan, variasi energi bebas Gibbs adalah ΔG = ΔH - T ΔS. Dalam proses seperti itu, (g) mewakili energi yang tersedia dalam sistem yang dapat menjadi pekerjaan.

Misalnya, dalam reaksi kimia eksotermik, entalpi berkurang saat entropi meningkat. Dalam fungsi Gibbs, kedua faktor ini ditimbulkan, tetapi hanya ketika energi Gibbs mengurangi reaksi terjadi secara spontan.

Jadi, jika variasi G negatif, prosesnya spontan. Saat fungsi Gibbs mencapai minimum, sistem mencapai keseimbangan yang stabil. Singkatnya, dalam proses di mana tekanan dan suhu tetap konstan yang dapat kita tegaskan:

- Jika prosesnya spontan, maka ΔG < 0

- Saat sistem seimbang: ΔG = 0

- Dalam proses non-spontan, ia meningkat: ΔG> 0.

[TOC]

Bagaimana itu dihitung?

Gibbs Free Energy (G) dihitung dengan definisi yang diberikan di awal:

G = h - t⋅s

Pada gilirannya, entalpi h adalah potensi termodinamika yang didefinisikan sebagai:

H = u + p v

- Selangkah demi selangkah

Selanjutnya, analisis langkah -dengan langkah akan dilakukan, untuk mengetahui variabel independen yang energi Gibbs adalah suatu fungsi:

1- Hukum Termodinamika Pertama, energi internal terkait dengan entropi sistem dan volume V untuk proses reversibel melalui hubungan diferensial:

Itu dapat melayani Anda: ethidium bromide: struktur, sifat, penggunaan, toksisitas

du = dq - dw = tds - pdv

Dari persamaan ini mengikuti bahwa energi internal U adalah fungsi dari variabel S dan V:

U = u (s, v)

2- Mulai dari definisi H dan mengambil diferensial diperoleh:

dh = du + d (p v) = du + vdp + pdv

3- Mengganti ekspresi untuk DU yang diperoleh dalam (1) Anda harus:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Dari sini disimpulkan bahwa entalpi h tergantung pada entropi dan tekanan p, yaitu:

H = h (s, p)

4- Sekarang total diferensial energi bebas Gibbs dihitung mendapatkan:

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Di mana DH telah digantikan oleh ekspresi yang ditemukan di (3).

5- Akhirnya, dengan menyederhanakan Anda mendapatkan: DG = VDP - SDT, Jelas bahwa energi bebas G tergantung pada tekanan dan suhu T sebagai:

G = g (p, t)

- Hubungan Termodinamika Maxwell

Dari analisis di bagian sebelumnya, ia mengikuti energi internal suatu sistem adalah fungsi dari entropi dan volume:

U = u (s, v)

Lalu diferensial ATAU menjadi:

du = ∂_SU |_V Ds + ∂_VU |_S DV = TDS - PDV

Dari ekspresi ini dalam turunan parsial, hubungan termodinamika Maxwell yang disebut SO dapat disimpulkan. Turunan parsial berlaku ketika suatu fungsi tergantung pada lebih dari satu variabel dan mudah dihitung dengan menerapkan teorema bagian berikut.

Hubungan Pertama Maxwell

 ∂_VT |_S = -Mon_SP |_V 

Untuk sampai ke hubungan ini, Clairaut Theorem - Schwarz pada turunan parsial, yang menyatakan hal berikut:

"Turunan campuran urutan kedua dengan variabel yang dipertukarkan adalah sama, asalkan fungsi yang akan diturunkan adalah kontinu dan berbeda".

Hubungan Kedua Maxwell

Mulai dari apa yang ditunjukkan pada poin 3 dari bagian sebelumnya:

Dapat melayani Anda: faktor yang mempengaruhi kelarutan

H = H (S, P) dan DH = TDS + VDP

Bisa didapatkan:

 ∂_PT |_S = ∂_SV |_P 

Lanjutkan dengan cara yang sama dengan energi bebas Gibbs G = g (p, t) Dan dengan energi bebas Helmholtz F = f (t, v) Untuk mendapatkan dua hubungan termodinamika Maxwell lainnya. 

Gambar 2. Josiah Gibbs (1839-1903) adalah seorang ahli fisika, ahli kimia, dan ahli matematika yang memberikan kontribusi besar bagi termodinamika. Sumber: Wikimedia Commons.

Empat hubungan termodinamika Maxwell 

1- terkait dengan energi internal U: ∂_VT |_S = -Mon_SP |_V

2- yang diperoleh dari entalpi h: ∂_PT |_S = ∂_SV |_P 

3- Terkait dengan energi Helmholtz f: ∂_TP |_V = ∂_VS |_T 

4- Terkait dengan energi bebas Gibbs G: ∂_TV |_P = -Mon_PS |_T

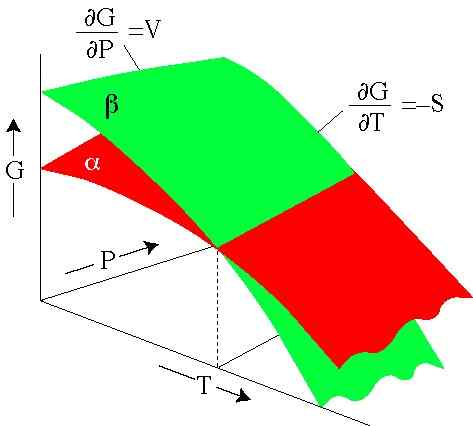Gambar 2. Energi Gibbs tergantung pada tekanan dan suhu. Setiap permukaan mewakili fase. (Serc.Carleton.Edu)

Latihan terpecahkan

Latihan 1

Hitung variasi energi bebas Gibbs untuk 2 mol gas ideal pada suhu 300k selama ekspansi isotermal yang mengarah ke sistem volume awal 20 liter ke volume akhir 40 liter.

Larutan

Mengingat definisi energi bebas Gibbs adalah:

G = h - t s

Maka variasi f yang terbatas adalah:

ΔG = ΔH - T ΔS, karena Δt = 0

Dalam gas ideal entalpi hanya tergantung pada suhu absolutnya, tetapi karena itu adalah proses isotermal, maka ΔH = 0 dan ΔG = - T ΔS.

Untuk gas ideal, variasi entropi dari proses isotermal adalah: 

ΔS = nr ln (v₂/V₁)

Yang diterapkan pada kasus latihan ini yang kami miliki:

ΔS = 2 mol x 8.314 j/(k mol) x ln (40l/20l) = 11.53 j/k

Kemudian kita bisa mendapatkan perubahan energi Helmholtz:

ΔG = - 300K x 11.53 j/k = -3457.70 j.

Latihan 2

Dengan mempertimbangkan bahwa energi bebas Gibbs adalah fungsi suhu dan tekanan G = g (t, p); Tentukan variasi G selama proses di mana suhu tidak berubah (isotermal) untuk n mol dari gas monoatomik yang ideal.

Dapat melayani Anda: strontium hidroksida (sr (oh) ₂)

Larutan

Seperti yang ditunjukkan di atas, perubahan energi Gibbs hanya tergantung pada perubahan suhu T dan volume V, sehingga variasi infinitesimal dihitung menurut:

Dg = -sdt + vdp

Tetapi jika itu adalah proses di mana suhu konstan maka df = + VDP, sehingga variasi terbatas tekanan ΔP menyebabkan perubahan energi Gibbs yang diberikan oleh:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Menggunakan persamaan gas yang ideal:

P v = n r t

Selama proses isotermal itu terjadi bahwa:

D (p v) = p dv + v dp = 0

Itu adalah:

dp/p = - dv/v

Jadi hasil sebelumnya dapat ditulis tergantung pada variasi volume ΔV:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Latihan 3

Mempertimbangkan reaksi kimia berikut:

N₂0 (g) + (3/2) atau₂ (g) ↔️No₂ (g) pada suhu t = 298 k

Temukan variasi energi bebas Gibbs dan melalui hasil yang diperoleh, tunjukkan apakah itu proses spontan atau tidak.

Larutan

Di bawah langkah:

- Langkah Pertama: Entri Reaksi

ΔHR = 2*ΔH (tidak₂ (g)) - ΔH (n₂0 (g)) = 2*33.2-81.6 = -15.2kj/mol

- Langkah Kedua: Variasi entropi reaksi

ΔSr = 2*s (tidak₂ (g)) - s (n₂0 (g)) - (3/2) S (atau₂ (g)) = 2*240.1 - 220.1 - 1.5*205.2 = -47.7 j/(mol*k).

- Langkah Ketiga: Variasi dalam Fungsi Gibbs

Nilai ini akan menentukan keseimbangan antara penurunan energi dan peningkatan entropi untuk mengetahui apakah reaksi akhirnya spontan atau tidak.

Δgr = ΔHr -t ΔSr = -15.2 -298*(-47.7) = -985.4 j/mol

Karena ini adalah variasi negatif dari energi Gibbs dapat disimpulkan bahwa itu adalah reaksi spontan pada suhu 298 K = 25 ºC.

Referensi

1. Castaños e. Latihan energi gratis. Pulih dari: lidiaconlachimica.WordPress.com.
2. Cengel, dan. 2012. Termodinamika. Edisi ke -7. Bukit McGraw.
3. Librettexts. Energi bebas Gibbs. Pulih dari: chem.Librettexts.org
4. Librettexts. Apa Energi Gratis. Pulih dari: chem.Librettexts.org
5. Wikipedia. Energi bebas Gibbs. Pulih dari: is.Wikipedia.com
6. Wikipedia. Energi bebas Gibbs. Diperoleh dari: di.Wikipedia.com