Unit energi bebas helmholtz, bagaimana itu dihitung, latihan terpecahkan

Itu Energi bebas Helmholtz Ini adalah potensi termodinamika yang mengukur pekerjaan yang berguna dari sistem tertutup dalam kondisi suhu dan volume yang konstan. Energi bebas Helmholtz dilambangkan F Dan didefinisikan sebagai perbedaan dari energi internal ATAU lebih sedikit produk suhu T Untuk entropi S:

F = u - t⋅s

Karena itu adalah energi, ia diukur dalam joule dalam sistem internasional (SI), meskipun unit lain yang sesuai juga dapat berupa ergio (CGS), kalori atau volt elektron (EV).

Gambar 1. Definisi energi Helmholtz. Sumber: Pixabay.

Variasi negatif energi Helmholtz selama proses disamakan dengan pekerjaan maksimum yang dapat dilakukan sistem dalam proses isokorik, yaitu volume konstan. Saat volume tidak konstan, bagian dari pekerjaan ini dapat dilakukan di lingkungan.

Dalam hal ini kami merujuk pada pekerjaan di mana volume tidak bervariasi, seperti pekerjaan listrik: DW = φdq, dengan φ sebagai potensi listrik dan Q sebagai muatan listrik.

Jika suhunya juga konstan, energi Helmholtz diminimalkan ketika keseimbangan tercapai. Untuk semua ini, energi Helmholtz sangat berguna dalam proses volume konstan. Dalam hal ini Anda memiliki:

- Untuk proses spontan: Δf < 0

- Saat sistem dalam keseimbangan: Δf = 0

- Dalam proses non-spontan: Δf> 0.

[TOC]

Bagaimana energi bebas helmholtz dihitung?

Seperti yang dinyatakan pada awalnya, energi Helmholtz didefinisikan sebagai "energi atau sistem internal, kecuali produk dari sistem suhu T absolut, oleh entropi sistem":

F = u - t⋅s

Itu adalah fungsi dari suhu t dan volume v. Langkah -langkah untuk memvisualisasikan ini adalah sebagai berikut:

Dapat melayani Anda: elektron internal

- Mulai dari hukum termodinamika pertama, energi internal atau terkait dengan entropi sistem dan volume V untuk proses reversibel melalui hubungan diferensial berikut:

du = dq - dw = tds - pdv

Ini mengikuti energi internal atau fungsi variabel S Dan V, Karena itu:

U = u (s, v)

- Sekarang definisi F Dan itu diturunkan:

df = du - d (ts) = du - tds - sdt

- Mengganti di sana ekspresi diferensial yang diperoleh untuk DU pada langkah pertama, tetap:

Df = tds - pdv - tds - sdt = -sdt - pdv

- Akhirnya, disimpulkan bahwa F adalah fungsi dari suhu T dan volume V dan dapat dinyatakan sebagai:

F = f (t, v)

Gambar 2. Hermann von Helmholtz (1821-1894), fisikawan dan dokter Jerman, diakui atas kontribusinya terhadap elektromagnetisme dan termodinamika, di antara bidang sains lainnya. Sumber: Wikimedia Commons.

Proses spontan

Energi Helmholtz dapat diterapkan sebagai kriteria umum spontanitas dalam sistem yang terisolasi, tetapi sebelum beberapa konsep harus ditentukan:

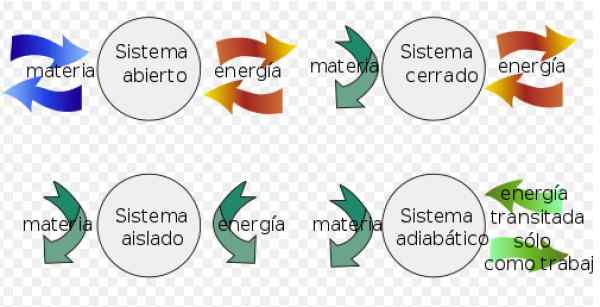
- A sistem ditutup Itu dapat bertukar energi dengan lingkungan, tetapi tidak dapat bertukar materi.

- Sebagai gantinya a sistem terisolasi tidak bertukar materi atau energi dengan lingkungan.

- Akhirnya a Sistem terbuka pertukaran materi dan energi dengan lingkungan. 

Gambar 3. Sistem termodinamika. Sumber: Wikimedia Commons. Fjgar (bis) [cc by-sa (https: // createveCommons.Org/lisensi/by-sa/4.0)].

Dalam proses reversibel, variasi energi internal dihitung sebagai berikut:

DU = TDS - PDV

Sekarang misalkan proses volume konstan (isocoric), di mana istilah kedua dari ekspresi sebelumnya memiliki kontribusi nol. Juga harus diingat bahwa menurut Ketidaksetaraan Clausius: 

ds ≥ dq/t

Ketidaksetaraan seperti itu berlaku untuk sistem termodinamika yang terisolasi.

Sehingga untuk suatu proses (reversibel atau tidak) di mana volume dipertahankan konstan dipenuhi:

Dapat melayani Anda: asam fosfat (H3PO4)

T ds ≥ du (Pada volume tetap)

Mempertimbangkan bahwa:

df = du - t ds 

Kita harus dalam proses isokoris pada suhu konstan terpenuhi bahwa: DF ≤ 0, seperti yang ditunjukkan di awal.

Sehingga energi Helmholtz F adalah jumlah penurunan dalam proses spontan saat ini adalah sistem yang terisolasi. F mencapai nilai minimum dan stabil ketika saldo reversibel telah tercapai.

Latihan terpecahkan

Latihan 1

Hitung variasi energi bebas helmholtz F untuk 2 mol gas ideal pada suhu 300K selama ekspansi isotermal yang mengarah ke sistem volume awal 20 liter hingga volume akhir 40 liter.

Larutan

Mulai dari definisi f:

F = u - t s

Kemudian variasi terbatas F, yang disebut ΔF, akan menjadi: akan menjadi:

ΔF = ΔU - T ΔS

Karena pernyataan tersebut menyatakan bahwa suhunya konstan: Δt = 0. Namun, dalam gas ideal energi internal hanya tergantung pada suhu absolutnya, tetapi karena itu adalah proses isotermal, maka ΔU = 0 Dan Δf = - t ΔS. Untuk gas ideal, variasi entropi dari proses isotermal ditulis seperti ini: 

ΔS = n.R.ln (v₂/V₁)

Menerapkan ungkapan ini:

ΔS = 2 mol x 8.314 j/(k mol) x ln (40l/20l) = 11.53 j/k

Akhirnya, perubahan energi Helmholtz adalah:

ΔF = - T ΔS = - 300K x 11.53 J/k = -3457.70 j.

Latihan 2

Di dalam silinder ada piston yang membaginya menjadi dua bagian dan di setiap sisi piston ada N mol gas monoatomik yang ideal, seperti yang ditunjukkan pada gambar di bawah ini.

Dinding silinder adalah konduktor panas yang baik (diatermis) dan bersentuhan dengan reservoir suhu T_{salah satu}.

Volume awal dari masing -masing bagian silinder adalah V_1i dan v_2i, sedangkan volume terakhirnya adalah V_1f dan v_2f Setelah perpindahan quasiescatik. Piston bergerak melalui plunger yang secara hermetis melintasi dua tapas silinder.

Itu dapat melayani Anda: Tecnecio (TC): Struktur, Properti, Penggunaan, Mendapatkan

Itu diminta untuk menemukan:

a) Perubahan energi internal gas dan pekerjaan yang dilakukan oleh sistem dan

b) variasi energi Helmholtz.

Solusi untuk

Saat piston bergerak secara quisiesterally, gaya eksternal yang diterapkan pada plunger harus menyeimbangkan gaya karena perbedaan tekanan dalam dua bagian silinder.

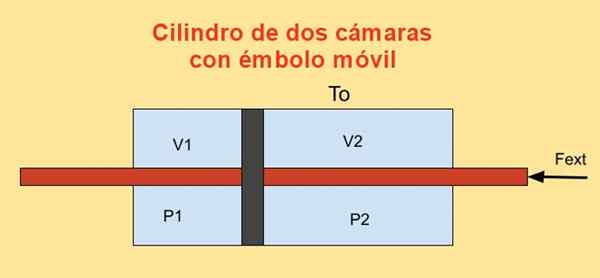Gambar 4. Variasi energi bebas f dalam silinder dengan dua kamera. Sumber: f. Zapata.

Pekerjaan Dw Dibuat oleh kekuatan eksternal F_ext Selama perpindahan yang sangat kecil Dx adalah:

Dw = - f_ext Dx = (p₁ - P₂) A dx = p₁ Dv₁ + P₂ Dv₂

Dimana hubungan telah digunakan Dv₁ = - dv₂ = A dx, makhluk ke Area piston. Di sisi lain, variasi energi Helmholtz adalah: 

Df = -sdt - pdv

Karena selama proses suhu tidak berubah, maka dt = 0 Dan Df = - pdv. Menerapkan ekspresi ini untuk setiap bagian silinder yang Anda miliki:

DW = p₁ Dv₁ + P₂ Dv₂ = - df₁ - Df₂

Makhluk F₁  Dan F₂ Energi Helmholtz di masing -masing kamera.

Pekerjaan W hingga dapat dihitung dari variasi terbatas energi Helmholtz dari setiap kamera:

W = -Δf₁ - Δf₂

Solusi b

Untuk menemukan perubahan energi dari Helmholtz, definisi digunakan: F = u - t s. Seperti di setiap kamera, Anda memiliki gas monoatomik yang ideal pada suhu konstan T_{salah satu}, Energi internal tidak berubah (ΔU = 0), sehingga: Δf = - t_{salah satu} ΔS. Di samping itu:

ΔS = nr ln (v_F/Gergaji)

Bahwa dengan menggantinya akhirnya memungkinkan pekerjaan yang dilakukan adalah: 

W = -t_{salah satu} Nr ln (v_1f /V_1i) -To nr ln (v_2f /V_2i) = -Δf₁ -Δf₂

W = - ke nr ln [(v_1f ⋅ V_1i)/(V_{2f .}V_2i)] = - Δf_total

Makhluk Δf_total Variasi total energi Helmholtz.

Referensi

1. Castaños e. Latihan energi gratis. Pulih dari: lidiaconlachimica.WordPress.com
2. Librettexts. Energi Helmholtz. Pulih dari: chem.Librettexts.org
3. Librettexts. Apa Energi Gratis. Pulih dari: chem.Librettexts.org
4. Wikipedia. Energi Helmholtz. Pulih dari: is.Wikipedia.com
5. Wikipedia. Energi bebas Helmholtz. Diperoleh dari: di.Wikipedia.com