Rumus dan persamaan kesalahan acak, perhitungan, contoh, latihan

Dia Kesalahan acak dari jumlah fisik terdiri dari variasi yang tidak dapat diprediksi dari ukuran jumlah itu. Variasi ini dapat dihasilkan oleh fenomena yang diukur, dengan instrumen pengukur atau oleh pengamat itu sendiri.

Kesalahan seperti itu bukan karena fakta bahwa ada sesuatu yang salah selama percobaan, tetapi itu adalah kesalahan yang melekat dalam proses pengukuran atau fenomena yang dipelajari. Ini menyebabkan ukuran yang diukur kadang -kadang sedikit lebih besar dan terkadang sedikit lebih rendah, tetapi biasanya berosilasi di sekitar nilai sentral.

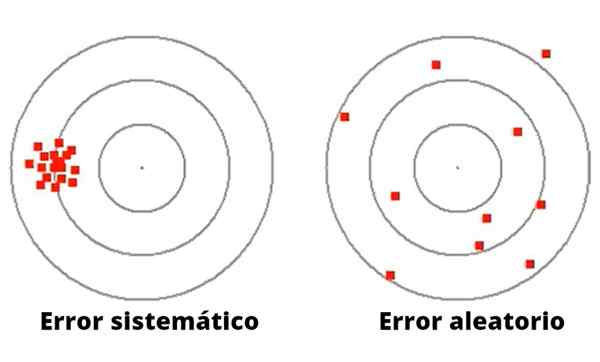
Gambar 1- Kesalahan acak bervariasi dalam besarnya dan arah. Sebaliknya, kesalahan sistematis cenderung konsisten.

Tidak seperti kesalahan acak, kesalahan sistematis dapat disebabkan oleh kalibrasi yang buruk atau faktor skala yang tidak tepat dalam instrumen pengukuran, termasuk kegagalan dalam peralatan eksperimental, atau pengamatan yang tidak tepat, yang menyebabkan penyimpangan dalam arti yang sama.

Gambar 1 menggambarkan perbedaan antara kesalahan sistematis dan acak dalam game peluncuran DART ke target dengan lingkaran.

Dalam kasus kiri anak panah terkonsentrasi di sekitar yang sangat jauh dari pusat. Pitcher anak panah ini, meskipun dengan tujuan yang baik, memiliki kegagalan sistematis, mungkin berasal dari visual, atau dalam cara melempar.

Di sisi lain, pitcher di sebelah kanan (pada Gambar 1) memiliki dispersi yang bagus di sekitar target pusat, oleh karena itu adalah pelempar yang sangat tidak tepat, dengan tujuan yang buruk, yang secara tidak sengaja membuat kesalahan acak.

[TOC]

Rumus dan persamaan dalam kesalahan acak

Ketika proses pengukuran menunjukkan kesalahan acak, itu perlu.

Tentu saja, dalam setiap pengukuran perlu untuk berhati -hati bahwa kondisi di mana mereka dilakukan selalu sama.

Dapat melayani Anda: Hukum Faraday: Formula, Unit, Eksperimen, Latihan,

Misalkan pengukuran diulangi N waktu. Karena ada kesalahan acak dalam setiap pengukuran akan ada nilai yang sedikit berbeda. Misalkan set N Pengukuran adalah:

X₁, X₂, X₃,…, X_N

Jadi apa nilai laporan untuk diukur? 

Nilai rata-rata dan standar deviasi

Itu nilai tengah salah satu rata-rata dari serangkaian tindakan, yang kami tunjukkan oleh dan dihitung sebagai berikut:

= (x₁ + X₂ + X₃ +... +x_N) / N

Deviasi standar

Namun, hasil ini memiliki margin kesalahan yang diberikan oleh standar deviasi. Untuk mendefinisikannya, Anda harus terlebih dahulu mengetahui penyimpangan dan kemudian varian:

-Penyimpangan D_yo  bahwa masing -masing nilai yang diukur memiliki Xi Mengenai nilai rata -rata adalah:

D_yo = x_yo -

Jika rata -rata penyimpangan dihitung, itu akan diperoleh secara sistematis = 0, mengingat bahwa: 

= (d₁ + D₂ + D₃ +... +d_N) /n =

= [x₁ - ) + (x₂ - ) +... +(x_N - )]/N

= (x₁+ X₂ +... + x_N) / n - n / n = - = 0

-Rata -rata penyimpangan tidak berguna untuk mengetahui dispersi tindakan. Di sisi lain, nilai rata -rata kuadrat penyimpangan atau varians, dilambangkan dengan σ², ya itu.

Itu dihitung sesuai dengan formula berikut:

σ² = (d₁² + D₂² +.. .+ D_N² ) / (N -1)

Dalam statistik jumlah ini disebut perbedaan.  

Dan pada akar kuadrat dari varian yang dikenal sebagai Deviasi standar σ:

σ = √ [(D₁² + D₂² +.. .+ D_N² ) / (n -1)] 

Deviasi standar σ menunjukkan bahwa:

1.- 68% pengukuran yang dilakukan termasuk dalam interval [ - σ, + σ]. 

2.- 95% pengukuran sedang dalam interval [ - 2σ, + 2σ].

3.- 99,7% dari tindakan yang diambil berada dalam kisaran [ - 3σ, + 3σ].

Cara menghitung kesalahan acak?

Hasil pengukuran adalah nilai tengah dari N Pengukuran yang dilambangkan dengan dan dihitung sesuai dengan rumus berikut:

Dapat melayani Anda: kecepatan areolar: bagaimana latihan itu dihitung dan diselesaikan

= (∑x_yo) / N

Namun, itu bukan nilai "tepat" dari pengukuran, karena dipengaruhi oleh Kesalahan acak ε, yang dihitung seperti ini:

ε = σ / √n

Di mana:

σ = √ [(∑ (xi -)² ) / (n -1)]

Hasil akhir dari pengukuran harus dilaporkan dengan cara berikut:

1. ± σ / √n = ± ε Dengan tingkat kepercayaan 68%.
2. ± 2σ / √n = ± 2ε Dengan tingkat kepercayaan 95%.
3. ± 3σ / √n = ± 3ε Dengan tingkat kepercayaan 99,7%.

Kesalahan acak mempengaruhi angka signifikan terakhir dari pengukuran, yang biasanya bertepatan dengan apresiasi instrumen pengukuran. Namun, jika kesalahan acak sangat besar, dua angka signifikan terakhir dapat dipengaruhi oleh variasi.

Contoh kesalahan acak

Kesalahan acak dapat muncul dalam berbagai kasus di mana suatu ukuran dibuat:

Mengukur panjang dengan pita pengukur atau aturan

Ketika panjang diukur dengan aturan atau pita pengukur dan pembacaan jatuh di antara merek skala, maka nilai menengah diperkirakan.

Terkadang estimasi memiliki kelebihan dan cacat lainnya, sehingga kesalahan acak sedang dimasukkan ke dalam proses pengukuran.

Gambar 2. Kesalahan acak mungkin muncul saat panjang diukur dengan pita pita. Sumber: Pikrepo.

Kecepatan angin

Dalam pengukuran kecepatan angin mungkin ada perubahan dalam membaca dari satu saat ke saat lainnya, karena perubahan sifat fenomena.

Saat membaca volume dalam silinder yang lulus

Ketika volume dibaca dengan silinder yang lulus, bahkan mencoba meminimalkan kesalahan paralase, setiap kali diukur, sudut pengamatan meniscal sedikit berubah sedikit, itulah sebabnya tindakan dipengaruhi oleh kesalahan acak.

Itu dapat melayani Anda: Kondisi keseimbangan pertama: Penjelasan, contoh, latihan Gambar 3.- Di laboratorium kimia dimungkinkan untuk membuat kesalahan acak dalam membaca silinder lulusan. Sumber: Pexels.

Saat perawakan anak diukur

Dengan mengukur ketinggian seorang anak, terutama jika agak gelisah, itu membuat perubahan postur kecil berubah sedikit berubah.

Saat menggunakan skala kamar mandi

Ketika kami ingin mengukur berat badan kami dengan kamar mandi, perubahan kecil pada titik dukungan, bahkan perubahan posisi dapat secara acak mempengaruhi pengukuran.

Olahraga diselesaikan

Kereta dorong mainan diizinkan untuk bergulir di sepanjang trek yang lurus dan miring dan diukur dengan stopwatch waktu yang mengambil seluruh trek. 

Pengukuran dilakukan 11 kali, dengan perawatan melepaskan gerobak dari tempat yang sama, tanpa memberikan dorongan hati dan menjaga perbaikan kecenderungan.

Hasil yang diperoleh adalah:

3,12S 3.09S 3.04S 3.04S 3.10S 3.08S 3.05S 3.10S 3.11S 3.06S, 3.03S

Apa kesalahan acak dari tindakan tersebut?

Gambar 4. Mengambil Waktu Mainan Kerajaan yang turun melalui pesawat miring. Sumber: Fanny Zapata.

Larutan

Seperti dapat dilihat, hasil yang diperoleh tidak unik dan sedikit bervariasi.

Yang pertama adalah menghitung nilai waktu penurunan rata -rata, memperoleh 3.074545455 detik.

Tidak masuk akal untuk mempertahankan begitu banyak desimal, karena setiap pengukuran memiliki tiga angka yang signifikan dan desimal kedua dari setiap ukuran tidak pasti, karena berada pada batas apresiasi stopwatch, oleh karena itu hasilnya dibulatkan menjadi dua desimal:

= 3.08 s.

Dengan kalkulator dalam mode statistik standar deviasi σ = 0,03 s Dan kesalahan standar adalah σ / √11 = 0,01 s. Hasil akhirnya dinyatakan sebagai berikut:

Waktu keturunan 

3,08 s ± 0,01s (dengan tingkat kepercayaan 68%)

3,08 s ± 0,02s (dengan tingkat kepercayaan 95%)

3,08 S ± 0,03s (dengan tingkat kepercayaan 99,7%)

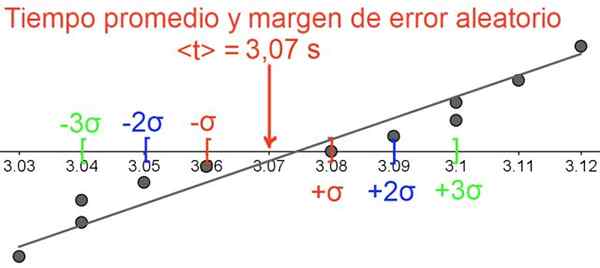Gambar 5. Margin kesalahan acak, perhatikan bahwa data dikelompokkan di sekitar nilai rata -rata. Sumber: f. Zapata.

Referensi

1. Canavos, g. 1988. Probabilitas dan Statistik: Aplikasi dan Metode. Bukit McGraw.
2. Devore, J. 2012. Probabilitas dan Statistik untuk Teknik dan Sains. Ke -8. Edisi. Cengage.
3. Helmestine a. Kesalahan acak Vs. Kesalahan sistematis. Pulih dari: thinkco.com
4. Laredo, e. Kesalahan tengah. Pulih dari: USB.pergi.
5. Levin, r. 1988. Statistik untuk administrator. 2nd. Edisi. Prentice Hall.