Fungsi trigonometri terbalik, turunannya, contoh, latihan

Itu Fungsi trigonometri terbalik, Seperti namanya, mereka adalah fungsi terbalik yang sesuai dari sinus, cosinus, garis singgung, cotangent, pengeringan dan pemanen.

Fungsi trigonometri terbalik dilambangkan dengan nama yang sama dari fungsi trigonometri langsung yang sesuai ditambah awalan BUSUR. Dengan demikian:

1.- Arcsen (x) Ini adalah fungsi trigonometri terbalik dari fungsi dosa (x)

2.- Arccos (x) Ini adalah fungsi trigonometri terbalik dari fungsi cos (x)

3.- Arctan (x) Ini adalah fungsi trigonometri terbalik dari fungsi Tan (x)

4.- Arccot ​​(x) Ini adalah fungsi trigonometri terbalik dari fungsi COT (x)

5.- Arcsec (x) Ini adalah fungsi trigonometri terbalik dari fungsi dtk (x)

6.- ARCCSC (x) Ini adalah fungsi trigonometri terbalik dari fungsi CSC (x)

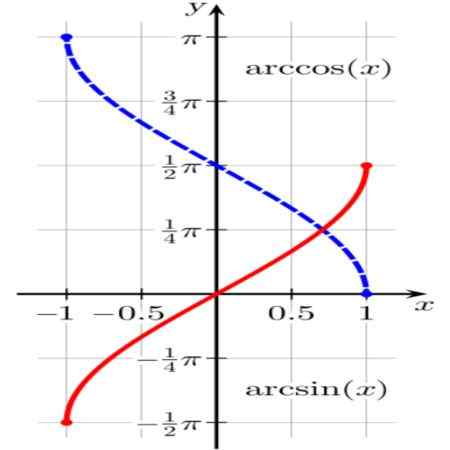
Gambar 1. Fungsi Arcsen (x) (berwarna merah) dan arccos (x) (berwarna biru). Sumber: Wikimedia Commons.

Fungsinya θ = arcsen (x) Itu menghasilkan unit busur θ (atau sudut di Radianes θ) seperti yang sin (θ) = x.

Jadi, misalnya, Arcsen (√3/2) = π/3 karena seperti yang diketahui, payudara radian π/3 sama dengan √3/2.

[TOC]

Nilai utama fungsi trigonometri terbalik

Sehingga fungsi matematika f (x) memiliki kebalikan g (x) = f^-1(x) perlu bahwa fungsi ini Suntikan, Yang berarti bahwa setiap nilai dan set kedatangan fungsi f (x) berasal dari satu dan hanya nilai x.

Jelas bahwa persyaratan ini tidak dipenuhi oleh fungsi trigonometri apa pun. Untuk mengklarifikasi intinya, mari kita perhatikan bahwa nilai y = 0,5 dapat diperoleh dari fungsi sinus dengan cara berikut:

• sin (π/6) = 0,5
• sin (5π/6) = 0,5
• sin (7π/6) = 0,5

Dan banyak lagi, karena fungsi sinus periodik dengan periode 2π.

Itu dapat melayani Anda: kelipatan 8: apa itu dan penjelasan

Untuk mendefinisikan fungsi trigonometri terbalik, perlu untuk membatasi domain fungsi trigonometri langsung yang sesuai, sehingga mereka memenuhi persyaratan injektif.

Domain terbatas fungsi langsung ini akan menjadi rentang utama atau cabang dari fungsi terbalik yang sesuai.

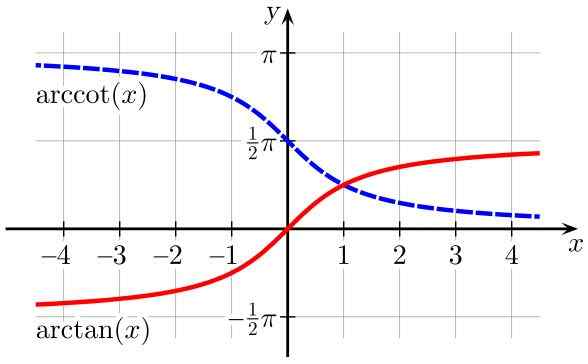Gambar 2. Fungsi arctan (x) (berwarna merah) dan arccot ​​(x) (berwarna biru). Sumber: Wikimedia Commons.

Tabel Domain dan Rentang Fungsi Trigonometri Terbalik

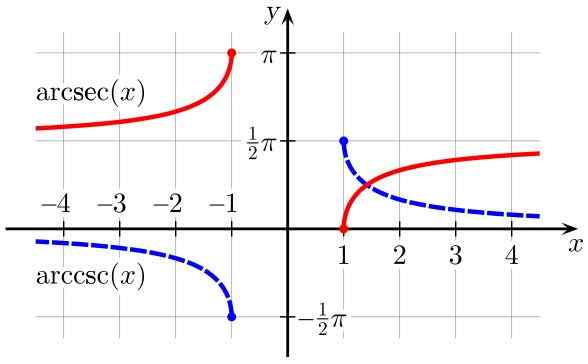Gambar 3. Fungsi arcsec (x) (merah) dan arccsc (x) (biru) (berwarna biru). Sumber: Wikimedia Commons.

Berasal dari fungsi trigonometri terbalik

Untuk mendapatkan turunan dari fungsi trigonometri terbalik, sifat -sifat turunannya diterapkan, khususnya yang berasal dari fungsi terbalik.

Jika kita menunjukkan untuk f (y) ke fungsi dan dengan f^-1(x) ke fungsi terbaliknya, maka yang berasal dari fungsi sebaliknya terkait dengan turunan fungsi langsung melalui hubungan berikut:

[F^-1(x)] '= 1/ f' [f^-1(X)]

Misalnya: jika x = f (y) = √y adalah fungsi langsung, kebalikannya akan

y = f^-1(x) = x². Mari kita terapkan aturan turunan terbalik untuk kasus sederhana ini untuk melihat bahwa aturan ini terpenuhi:

[X²] '= 1 / [√y]' = 1 / (½ dan^-½ = 2 dan^½ = 2 (x²)^½ = 2x 

Nah, kita dapat menilai trik ini untuk menemukan yang berasal dari fungsi trigonometri terbalik.

Misalnya, kami ambil θ = arcsen (x) Sebagai fungsi langsung, maka fungsi terbaliknya sin (θ) = x.

[arcsen (x)] '= 1 / [sin (θ)]' = 1 / cos (θ) = 1 / √ (1 - sen (θ)²) = ..

… = 1 / √ (1 - x²) .

Dengan cara ini, semua yang berasal dari fungsi trigonometri terbalik dapat diperoleh, yang ditunjukkan di bawah ini:

Gambar 4. Tabel yang berasal dari fungsi trigonometri terbalik. Sumber: Wikimedia Commons.

Derivatif ini berlaku untuk setiap argumen z yang termasuk dalam angka kompleks dan karenanya juga berlaku untuk argumen nyata x, karena z = x + 0i.

Dapat melayani Anda: segi empat: elemen, properti, klasifikasi, contoh

Contoh

- Contoh 1

Temukan Arctan (1).

Larutan

Arctan (1) adalah unit busur (sudut dalam radianes) ፀ sedemikian rupa sehingga tan (ፀ) = 1. Sudut itu adalah ፀ = π/4 karena SO (π/4) = 1. Kemudian Arctan (1) = π/4.

- Contoh 2

Hitung Arcsen (cos (π/3)).

Larutan

Sudut π/3 radian adalah sudut terkenal yang kosinusnya ½, sehingga masalahnya dikurangi menjadi menemukan arcsen (½).

Jadi ini tentang menemukan sudut yang sininya memberi ½. Sudut itu π/6, karena sen (π/6) = sen (30º) = ½. Oleh karena itu arcsen (cos (π/3)) = π/6. 

Latihan

- Latihan 1

Temukan hasil dari ekspresi berikut:

Sec (Arcan (3)) + CSC (Arccot ​​(4))

Larutan

Kami mulai memberi nama α = arcan (3) dan β = arcot (4). Jadi ekspresi yang harus kita hitung adalah seperti ini:

SEC (α) + CSC (β)

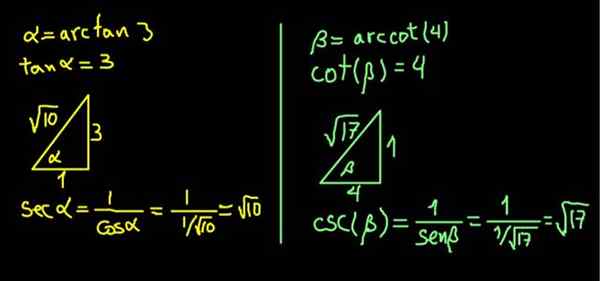
Ekspresi α = arcan (3) setara dengan mengatakan begitu (α) = 3.

Karena garis singgung adalah kaki yang berlawanan pada yang berdekatan, segitiga persegi panjang cateto yang bertentangan dengan α dari 3 unit dan kategori 1 unit yang berdekatan dibangun, sehingga demikian (α) = 3/1 = 3.

Dalam segitiga persegi panjang, hipotenus ditentukan oleh teorema Pythagoras. Dengan nilai -nilai ini √10, sehingga:

Sec (α) = Cateto yang berdekatan / berdekatan = √10 / 1 = √10.

Demikian pula β = arcot (4) setara dengan menyatakan bahwa cot (β) = 4.

Segitiga persegi panjang dari cateto yang berdekatan dengan β dari 4 unit dan cateto yang berlawanan dari 1 unit dibangun, sehingga COT (β) = 4/1.

Segitiga segera selesai menemukan hipotenusinya berkat teorema Pythagoras. Dalam hal ini ternyata memiliki √17 unit. Kemudian CSC (β) = cateto hypotenuse / berlawanan = √17 / 1 = √17 dihitung.

Itu dapat melayani Anda: y = 3sen (4x) periode fungsi

Mengingat bahwa ekspresi yang harus kita hitung adalah: 

SEC (ARCAN (3)) + CSC (ARCOT (4)) = Sec (α) + CSC (β) =…

… = √10 + √17 = 3.16 + 4.12 = 7,28.

- Latihan 2

Temukan solusi dari:

Cos (2x) = 1 - sen (x)

Larutan

Diperlukan bahwa semua fungsi trigonometri diekspresikan dalam argumen atau sudut yang sama. Kami akan menggunakan identitas sudut ganda:

Cos (2x) = 1 - 2 sen²(X)

Maka ekspresi asli dikurangi menjadi:

1 - 2 sen²(x) = 1 - sin x

Setelah disederhanakan dan diperkaktifkan, itu dinyatakan sebagai:

sin (x) (2 sen (x) - 1) = 0

Yang memunculkan dua persamaan yang mungkin: sin (x) = 0 dengan solusi x = 0 dan persamaan lain sen (x) = ½ dengan x = π/6 sebagai solusi.

Solusi untuk persamaan yang diangkat adalah: x = 0 atau x = π/6.

- Latihan 3

Temukan solusi dari persamaan trigonometri berikut:

cos (x) = dosa²(X)

Larutan

Untuk menyelesaikan persamaan ini, lebih mudah untuk menempatkan satu jenis fungsi trigonometri, jadi kami akan menggunakan identitas trigonometri mendasar sehingga persamaan asli ditulis ulang sebagai berikut:

cos (x) = 1 - cos²(X)

Jika kami menyebutkan y = cos (x), ekspresi dapat ditulis ulang sebagai:

Dan² + dan - 1 = 0

Ini adalah persamaan tingkat kedua dalam dan, yang solusinya adalah:

y = (-1 ± √5) / 2

Maka nilai -nilai x yang memenuhi persamaan asli adalah:

x = arcos ((-1 ± √5) / 2)

Solusi sebenarnya adalah tanda positif x = 0,9046 rad = 51,83º.

Solusi lainnya kompleks: x = (π - 1.06 i) rad.

Referensi

1. Hazewinkel, m. 1994. Encyclopaedia of Mathematics. Kluwer Academic Publishers / Springer Science & Business Media. 
2. Teman seluler. Fungsi trigonometri terbalik. Pulih dari: matemovil.com
3. Rumus alam semesta. Fungsi trigonometri terbalik. Pulih dari: universoformulas.com
4. Weisstein, Eric W. Menciptakan fungsi trigonometri. Dipulihkan dari: MathWorld.Wolfram.com
5. Wikipedia. Menciptakan fungsi trigonometri. Diperoleh dari: di.Wikipedia.com