Upaya normal apa yang terdiri dari, bagaimana itu dihitung, contohnya

Dia upaya normal Diterapkan pada bahan tertentu, juga disebut upaya uniaksial, itu adalah hubungan antara gaya yang diterapkan tegak lurus dengan permukaan tertentu dan area silang -ectional di mana ia bertindak, atau beban per unit area area. Secara matematis, jika P adalah besarnya gaya dan A adalah area di mana ia diterapkan, upaya σ adalah hasil bagi: σ = p/a.

Unit upaya normal dalam sistem internasional adalah Newton /Metro², Dikenal sebagai Pascal dan Singkat PA. Ini adalah unit tekanan yang sama. Unit lain yang muncul dalam literatur sering kali pound / inci² salah satu psi.

Gambar 1. Batuan terus mengalami upaya karena aktivitas tektonik, menyebabkan deformasi di kerak bumi. Sumber: Pixabay.

Pada Gambar 2, dua kekuatan dengan besarnya diterapkan secara tegak lurus ke area silang -ectional, membuat traksi pada bilah yang sangat ringan yang cenderung memperpanjangnya.

Kekuatan -kekuatan ini menghasilkan upaya normal yang juga disebut Beban aksial terpusat, karena garis aksinya bertepatan dengan sumbu aksial, di mana centroid berada.

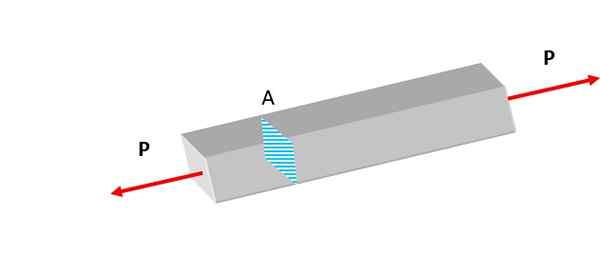Gambar 2. Bilah yang ditampilkan tunduk pada kekuatan traksi. Sumber: Made sendiri.

Upaya, apakah jenis normal atau lainnya, muncul terus menerus di alam. Di litosfer, batuan tunduk pada gravitasi dan aktivitas tektonik, percobaan percobaan.

Dengan cara ini struktur seperti lipatan dan kegagalan berasal, yang studinya penting dalam penggunaan mineral dan teknik sipil, untuk pembangunan bangunan dan jalan, untuk beberapa contoh.

[TOC]

Bagaimana itu dihitung?

Persamaan yang diberikan pada awal σ = P/A memungkinkan untuk menghitung upaya normal rata -rata pada area yang dimaksud. Nilai P adalah besarnya gaya yang dihasilkan di atas area yang diterapkan pada centroid dan cukup untuk banyak situasi sederhana.

Dalam hal ini, distribusi kekuatan seragam, terutama pada titik -titik jauh dari tempat Anda memiliki bilah yang dapat dikenakan traksi atau kompresi. Tetapi jika upaya tersebut diperlukan untuk menghitung pada titik tertentu atau kekuatan tidak didistribusikan secara merata, perlu menggunakan definisi berikut:

Dapat melayani Anda: sirkuit listrik tertutup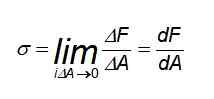

Kemudian secara umum, nilai upaya pada titik tertentu mungkin berbeda dari nilai rata -rata. Sebenarnya upaya tersebut dapat bervariasi sesuai dengan bagian yang perlu dipertimbangkan.

Ini diilustrasikan dalam gambar berikut, di mana kekuatan traksi f mencoba memisahkan bilah dalam kesetimbangan di bagian mm Dan nn.

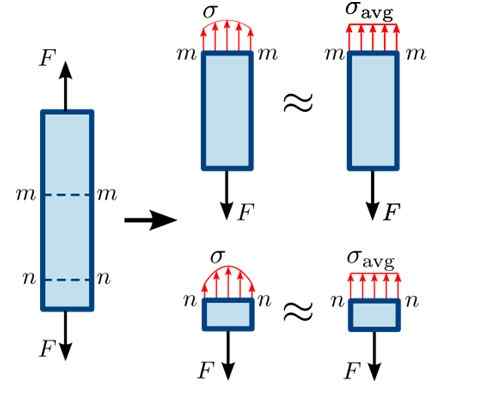Gambar 3. Distribusi upaya normal di berbagai bagian bar. Sumber: https: // commons.Wikimedia.org/wiki/file: Normal_Stress.SVG#/Media/File: Normal_Stress.SVG

Sebagai bagian nn Sangat dekat dengan di mana gaya F turun, distribusi gaya di permukaan tidak sepenuhnya homogen, anak di bawah umur ini semakin jauh dari titik itu. Distribusinya sedikit lebih homogen di bagian ini mm.

Bagaimanapun upaya normal selalu cenderung meregangkan atau mengompres dua bagian tubuh yang ditemukan di kedua sisi bidang tempat mereka bertindak. Di sisi lain, upaya lain yang berbeda, seperti geser, cenderung bergerak dan memisahkan bagian -bagian ini.

Hukum Hooke dan upaya normal

Hukum Hooke menyatakan bahwa dalam batas elastis, upaya normal berbanding lurus dengan deformasi yang dialami oleh batang atau objek. Dalam hal itu:

Upaya normal ∝ Deformasi kesatuan

Konstanta proporsionalitas menjadi modul muda (Y):

Upaya Normal (σ) = Modul Muda (Y) x Deformasi Kesatuan (ε)

σ = y. ε

Dengan ε = ΔL/L, di mana Δl adalah perbedaan antara final dan panjang awal, yaitu l.

Modul muda atau modul elastisitas adalah karakteristik material, yang dimensinya sama dengan upaya, karena deformasi unit tidak dimensi.

Itu dapat melayani Anda: 13 contoh hukum kedua Newton dalam kehidupan sehari -hari

Pentingnya upaya dalam resistensi bahan dan geologi

Menentukan seberapa tahan bahan upaya sangat penting. Untuk struktur yang digunakan dalam konstruksi bangunan, serta dalam desain bagian untuk perangkat yang berbeda, perlu untuk memastikan bahwa bahan yang dipilih dengan benar memenuhi fungsinya.

Oleh karena itu, bahan dianalisis secara mendalam di laboratorium melalui uji coba yang ditakdirkan untuk mengetahui berapa banyak kekuatan yang dapat mereka lawan sebelum mendeformasi dan melanggar, sehingga kehilangan fungsi mereka. Berdasarkan hal ini, keputusan tersebut dibuat apakah akan memproduksi bagian tertentu atau tidak atau menjadi bagian dari perangkat.

Dipercayai bahwa ilmuwan pertama yang secara sistematis mempelajari resistensi bahan adalah Leonardo da Vinci. Dia meninggalkan bukti uji coba di mana dia menentukan resistensi batu gantung kabel dari berbagai peso.

Dalam upaya baik besarnya gaya dan juga dimensi struktur dan bagaimana hal itu diterapkan adalah penting, untuk menetapkan batas -batas di mana material memiliki perilaku elastis; yaitu, ia kembali ke bentuk aslinya saat upaya berhenti.

Dengan hasil tes ini, kurva upaya-deformasi dilakukan untuk berbagai jenis bahan, seperti baja, beton, aluminium dan banyak lagi.

Contoh

Dalam contoh -contoh berikut diasumsikan bahwa kekuatan didistribusikan secara merata, dan bahwa bahannya homogen dan isotropik. Ini berarti propertinya sama di segala arah. Oleh karena itu valid untuk menerapkan persamaan σ = p/a untuk menemukan upaya.

-Latihan 1

Pada Gambar 3, diketahui bahwa upaya normal rata -rata yang bekerja pada bagian AB memiliki besarnya 48 kPa. Temukan: a) Besarnya gaya F yang bertindak dalam CB, b) upaya pada bagian BC.

Itu dapat melayani Anda: pemotretan horizontal: karakteristik, formula dan persamaan, latihan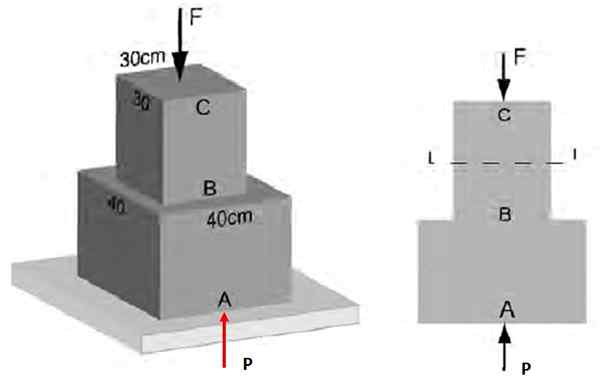Gambar 4. Upaya normal pada struktur contoh 1 ..

Larutan

Karena strukturnya berada dalam keseimbangan statis, menurut hukum kedua Newton:

P-f = 0

Upaya normal pada bagian AB memiliki besarnya:

σ_AB = P/a_AB

Dimana p = σ_AB . KE_AB = 48000 pa. (40 x 10 ^-2 M)² = 7680 n

Oleh karena itu f = 7680 n

Upaya normal pada bagian BC adalah rasio antara besarnya F dan luas penampang di sisi itu:

σ_Bc = F/a_Bc = 7680 N / (30 x 10 ^-2 M)² = 85.3 kPa.

-Latihan 2

Panjang kawat 150 m dan 2.Diameter 5 mm diregangkan oleh gaya 500 N. Menemukan:

a) Upaya longitudinal σ.

b) Deformasi kesatuan, mengetahui bahwa panjang akhir adalah 150.125 m.

c) Modul Elastisitas DAN dari kawat ini.

Larutan

a) σ = f / a = f / π.R²

Jari -jari kawat adalah setengah dari diameter:

R = 1.25 mm = 1.25 x 10^-3 M.

Area silang adalah π.R², Maka usahanya adalah:

σ = f / π.R² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 pa

b) ε = ΔL / L = (Panjang Akhir - Panjang Awal) / Panjang Awal

Karena itu:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Modul Young dari kawat dibersihkan dengan mengetahui nilai ε dan σ yang sebelumnya dihitung:

Y = σ / ε = 101859.2 pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPa.

Referensi

1. Bir, f. 2010. Mekanika Bahan. Ke -5. Edisi. Bukit McGraw. 7 - 9.
2. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6^Tth  Ed. Prentice Hall. 238-242.
3. Hibbeler, R.C. 2006. Mekanika Bahan. 6. Edisi. Pendidikan Pearson. 22 -25
4. Valera Negrete, J. 2005. Catatan Fisika Umum. Unam. 87-98.
5. Wikipedia. Stres (mekanika). Pulih dari: wikipedia.org.