Estimasi berdasarkan interval

Apa estimasi dengan interval?

Itu Estimasi berdasarkan interval Ini adalah cara untuk menentukan kisaran nilai di mana rata -rata populasi dapat dimasukkan, berdasarkan informasi sampel dengan ukuran terbatas, diekstraksi secara acak dari total populasi.

Dia Interval estimasi Lebih rendah karena sampel lebih besar, tetapi menjadi lebih luas jika level atau persentase reliabilitas meningkat yang sama.

Jika Anda ingin mengetahui rata -rata populasi dari variabel tertentu dalam bentuk yang tepat, maka total populasi harus dipertimbangkan, sesuatu yang tidak selalu layak, karena jika itu adalah populasi yang sangat besar, mahal untuk mendapatkan data dari seluruh populasi. Untuk alasan ini, satu atau lebih sampel acak dari total populasi digunakan untuk mengambil.

Ini didasarkan pada hipotesis bahwa, dengan mengekstraksi sampel acak, tidak bias dan mempertimbangkan secara proporsional semua strata, maka nilai rata -rata sampel harus sangat dekat dengan rata -rata populasi rata -rata populasi.

Logika menunjukkan bahwa semakin besar data sampel, perbedaan antara nilai sampel rata -rata dan nilai populasi rata -rata lebih rendah.

Interval estimasi

Dalam praktiknya, kecuali populasi lengkap diketahui, hanya mungkin untuk menemukan, dengan beberapa probabilitas, interval di mana rata -rata populasi dapat ditemukan, berdasarkan sampel dengan ukuran terbatas.

Dalam kasus populasi yang mengikuti distribusi normal, dengan Deviasi standar σ , itu Perbedaan standar Antara rata -rata populasi μ dan sampel ukuran rata -rata N diberikan oleh:

| μ - | ≤ σ / √n

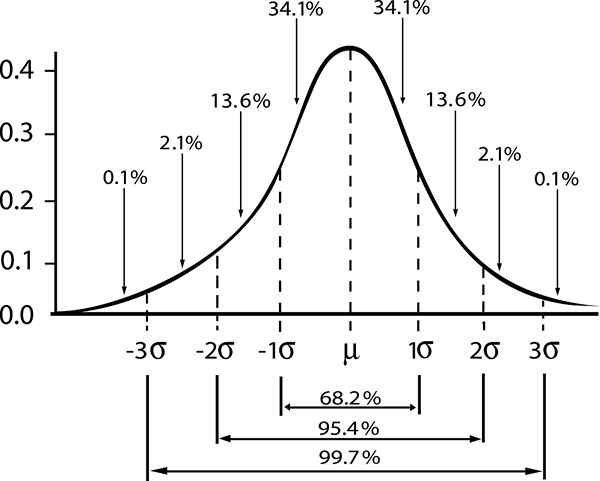
Di sini, kata "standar" menunjukkan bahwa 68% dari sampel ukuran N, Mereka memiliki nilai rata -rata antara interval [μ - σ / √n, μ + σ / √n].

Dapat melayani Anda: Kriteria Divisibilitas: Apa itu, Apa Penggunaan dan Aturannya

Perkiraan Standar

Interpretasi alternatif dari hal di atas adalah mengatakan bahwa rata -rata populasi yang diperoleh dari sampel ukuran N dan nilai rata -rata dipahami dalam interval  [ - σ / √n, + σ / √n], Dengan probabilitas 68%.

Dalam kebanyakan kasus nyata, tidak mungkin untuk mengetahui penyimpangan populasi standar, jadi σ Itu diperkirakan dengan standar deviasi sampel S, yang dihitung sebagai berikut:

S = √ (∑ (x_yo - )² / √ (n-1).

Dari sana Anda mendapatkan interval yang bisa mengandung rata -rata populasi dengan tingkat kepercayaan 68% (tingkat kepercayaan standar), diberikan oleh:

  -s / √n ≤ μ ≤ + s / √n

Interval pengukuran populasi ini dikenal sebagai interval estimasi standar dan diperoleh hanya dengan data yang tersedia dalam ukuran N.

Dari formula sebelumnya, jika Anda ingin memperkuat interval estimasi menjadi dua, itu perlu melipatempatkan Ukuran sampel.

Estimasi dengan interval kepercayaan

Dalam studi tertentu, tingkat standar 68% tidak cukup, maka perlu untuk menentukan interval dengan tingkat kepercayaan yang sewenang -wenang γ.

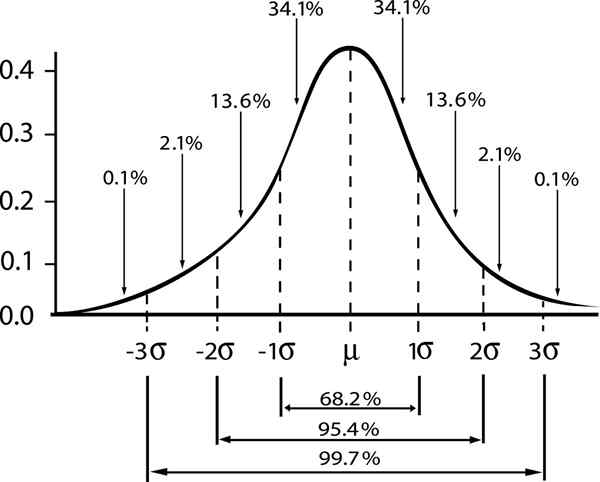Hubungan antara margin keandalan dan interval dalam distribusi Gaussian ditampilkan

Jika kami menunjukkan oleh ε Kesalahan standar s/√n, Kemudian kesalahan estimasi untuk tingkat kepercayaan diri γ akan diberikan oleh:

E = Zγ⋅ε.

Di mana Zγ Ini adalah angka yang dengannya kesalahan standar dikalikan, dan dengan demikian mendapatkan margin kesalahan dengan tingkat kepercayaan yang sewenang -wenang γ.

Untuk mendapatkan faktornya Zγ, lanjutkan sebagai berikut:

Itu dapat melayani Anda: bilangan rasional: properti, contoh dan operasi

Langkah 1

Adalah panggilannya tingkat signifikansi α sesuai dengan tingkat kepercayaan γ dengan formula berikut:

α = 1 - γ

Langkah 2

Nilainya ditentukan:

Ini adalah frekuensi akumulasi dalam distribusi normal yang ditiru N (0,1) Dalam interval (-∞, Zγ ].

Langkah 3

Itu jelas Zγ Persamaannya:

N (zγ) = 1 - α/2

Karena ini merupakan persamaan integral, izin ini diperoleh dari tabel distribusi normal, menggunakan metode interpolasi linier.

Langkah 4

Atau untuk penggunaan tabel, fungsi statistik yang dimasukkan dalam spreadsheet seperti Unggul, salah satu Sheet Google. Program -program ini menggabungkan fungsi terbalik normal N^-1, sehingga faktor koreksi Zγ Diperoleh secara langsung mengevaluasi fungsi terbalik ini:

Zγ = n^-1(1 - α/2).

Interval kepercayaan yang khas

Tingkat kepercayaan yang paling sering digunakan adalah:

• Zγ = 1; Tingkat kepercayaan standar γ = 0,68.
• Zγ = 2; tingkat kepercayaan diri γ = 0,95 (atau tingkat signifikansi 5%).
• Zγ = 3; tingkat kepercayaan diri γ = 0,997 (atau tingkat signifikansi 0,3%)

Contoh

Contoh 1

Tentukan interval berat rata -rata bayi baru lahir selama bulan Agustus di kota besar berdasarkan sampel acak 100 bayi, di mana berat rata -rata 3100 gram diperoleh dengan standar deviasi sampel s = 1500 gram.

Larutan

Pertama, kesalahan standar sampel ditentukan:

ε = s/√n = (1500 g)/√100 = 150 g.

Oleh karena itu, mulai dari sampel ini, dapat disimpulkan bahwa berat rata -rata bayi yang lahir pada bulan Agustus di kota itu adalah antara 2950 g dan 3250 g, dengan probabilitas 68%.

Contoh 2

Misalkan ukuran sampel bayi yang lahir pada bulan yang sama di bulan Agustus dan di kota yang sama dari Contoh 1. Berat sampel rata -rata adalah 3100 g dengan dispersi standar 1500 g. 

Itu dapat melayani Anda: dekomposisi bilangan alami (contoh dan latihan)

Itu diminta untuk memperkirakan interval berat rata -rata dari bayi baru lahir kota itu, dari sampel baru ini.

Larutan

Sekarang kesalahan standar berkurang pada faktor 1/√2, Jadi kesalahan standar baru dari berat rata -rata adalah 106 g.

Maka dapat diperkirakan, dari sampel baru ini bahwa, berat rata -rata bayi baru lahir terdiri dari kisaran 2994 g hingga 3206 g, dengan probabilitas 68%.

Latihan

Latihan 1

Tentukan kisaran berat rata -rata bayi baru lahir pada bulan Agustus, mulai dari sampel yang ditentukan dalam Contoh 1, dengan probabilitas 95%.

Larutan

Tingkat reliabilitas 95% menggandakan kisaran berat rata -rata, dibandingkan dengan tingkat reliabilitas 68%.

Oleh karena itu, berat rata -rata bayi baru lahir termasuk dalam kisaran 2800 gram pada 3400 gram dengan kepastian 95%.

Latihan 2

Perkirakan dengan tingkat kepercayaan 99,7% interval di mana berat rata -rata bayi baru lahir dari kota besar akan ditemukan, jika sampel tersedia dengan berat rata -rata 100 bayi yang sama dengan 3100 g, dan dengan deviasi sampel standar s = 1500 G.

Larutan

Margin kesalahan berat rata -rata, dengan 99,7% dari kepastian, akan menjadi tiga kesalahan rata -rata, yaitu:

3*1500/√100.

Kemudian disimpulkan, dari sampel ini, bahwa berat rata -rata bayi baru lahir akan dimasukkan dalam interval: 2650 gram hingga 3550 gram, dengan tingkat kepastian 99,7%. 

Dari hasil ini diamati dengan tingkat kepastian yang lebih besar meningkatkan ketidakpastian bobot rata -rata ke interval yang jauh lebih luas.