Aturan empiris bagaimana menerapkannya, untuk apa, latihan diselesaikan

A Aturan empiris Ini adalah hasil dari pengalaman praktis dan pengamatan kehidupan nyata. Misalnya, Anda dapat mengetahui bahwa spesies burung dapat diamati di tempat -tempat tertentu di setiap waktu tahun ini dan bahwa pengamatan dapat ditetapkan sebagai "aturan" yang menggambarkan siklus hidup burung -burung ini.

Dalam statistik, aturan empiris mengacu pada bentuk pengelompokan pengamatan di sekitar nilai sentral, rata -rata atau rata -rata, dalam unit standar deviasi.

Misalkan Anda memiliki sekelompok orang dengan tinggi rata -rata 1.62 meter dan standar deviasi 0.25 meter, maka aturan empiris akan memungkinkan untuk mendefinisikan, misalnya, berapa banyak orang dalam interval rata -rata kurang lebih standar deviasi?

Menurut aturan tersebut, 68% dari data kurang lebih merupakan standar deviasi rata -rata, yaitu, 68% dari kelompok orang akan memiliki ketinggian antara 1.37 (1.62-0.25) dan 1.87 (1.62+0.25) meter.

[TOC]

Dari mana aturan empiris berasal?

Aturan empiris adalah generalisasi teorema TCHEBYSHEV dan distribusi normal.

THEBYSHEV THEOREM

Teorema TcheByshev mengatakan bahwa: untuk beberapa nilai k> 1, probabilitas bahwa variabel acak adalah di antara rata -rata kurang k kali standar deviasi, dan rata -rata lebih k kali, standar deviasi lebih besar atau sama dengan (1 -1 /k²).

Keuntungan dari teorema ini adalah bahwa ia berlaku untuk variabel acak diskrit atau kontinu dengan distribusi probabilitas apa pun, tetapi aturan yang didefinisikan dari itu tidak selalu sangat tepat, karena tergantung pada simetri distribusi. Semakin asimetris distribusi variabel acak, kurang disesuaikan dengan aturan akan menjadi perilakunya.

Aturan empiris yang didefinisikan dari teorema ini adalah:

Jika k = √2, dikatakan bahwa 50% dari data berada dalam interval: [µ - √2 s, µ + √2 s]

Jika k = 2, dikatakan bahwa 75% dari data dalam interval: [µ - 2 s, µ + 2 s]

Jika k = 3, dikatakan bahwa 89% dari data dalam interval: [µ - 3 s, µ + 3 s]

Distribusi normal

Distribusi normal, atau bel Gauss, memungkinkan untuk menetapkan aturan empiris atau aturan 68 - 95 - 99.7.

Dapat melayani Anda: proporsi

Aturan ini didasarkan pada probabilitas terjadinya variabel acak pada interval antara rata -rata kurang satu, dua atau tiga standar deviasi dan rata -rata ditambah satu, dua atau tiga standar deviasi.

Aturan empiris mendefinisikan interval berikut:

68.27% dari data berada dalam interval: [µ - s, µ + s]

95.45% dari data berada dalam interval: [µ - 2s, µ + 2s]

99.73% dari data berada dalam interval: [µ - 3s, µ + 3s]

Pada gambar Anda dapat melihat bagaimana interval ini disajikan dan hubungan di antara mereka dengan meningkatkan lebar basis grafik.

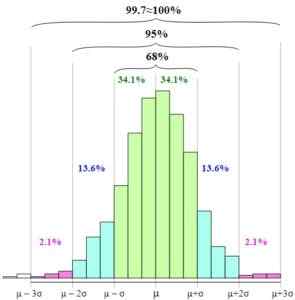Aturan empiris. Melikamp [cc by-sa 4.0 (https: // createveCommons.org/)] Standarisasi variabel acak, yaitu, ekspresi variabel acak dalam hal variabel standar atau normal, menyederhanakan penggunaan aturan empiris, karena variabel z memiliki rata -rata sama dengan nol dan standar deviasi yang sama untuk satu.

Oleh karena itu, penerapan aturan empiris pada skala variabel normal standar, z, mendefinisikan interval berikut:

68.27% dari data dalam interval: [-1, 1]

95.45% dari data dalam interval: [-2, 2]

99.73% data dalam interval: [-3, 3]

Bagaimana menerapkan aturan empiris?

Aturan empiris memungkinkan Anda menyingkat perhitungan saat bekerja dengan distribusi normal.

Misalkan sekelompok 100 mahasiswa memiliki usia rata -rata 23 tahun, dengan standar deviasi 2 tahun. Informasi apa yang diizinkan oleh aturan empiris?

Penerapan aturan empiris menyiratkan mengikuti langkah -langkah:

1- Bangun interval aturan

Karena rata -rata adalah 23 dan standar deviasi adalah 2, maka intervalnya adalah:

[µ - s, µ + s] = [23 - 2, 23 + 2] = [21, 25]

[µ - 2s, µ + 2s] = [23 - 2 (2), 23 + 2 (2)] = [19, 27]

[µ - 3s, µ + 3s] = [23 - 3 (2), 23 + 3 (2)] = [17, 29]

2- Hitung jumlah siswa dalam setiap interval sesuai dengan persentase

(100)*68.27% = 68 siswa kira -kira

(100)*95.45% = sekitar 95 siswa

(100)*99.73% = 100 siswa

3- Interval usia dikaitkan dengan jumlah siswa dan ditafsirkan

Setidaknya 68 siswa berusia antara 21 dan 25 tahun.

Dapat melayani Anda: statistik deskriptif: sejarah, karakteristik, contoh, konsep

Setidaknya 95 siswa berusia antara 19 dan 27 tahun.

Hampir 100 siswa berusia antara 17 dan 29 tahun.

Untuk apa aturan empirisnya?

Aturan empiris adalah cara cepat dan praktis untuk menganalisis data statistik, semakin andal sejauh distribusi dekat dengan simetri.

Kegunaannya tergantung pada bidang di mana ia digunakan dan pertanyaan yang muncul. Sangat berguna untuk mengetahui bahwa terjadinya nilai tiga standar deviasi hampir tidak mungkin di bawah atau di atas rata -rata, bahkan untuk variabel distribusi non -normal, setidaknya 88.8% kasus berada dalam interval tiga sigma.

Dalam ilmu sosial, hasil yang umumnya konklusif adalah interval dari rata -rata lebih atau kurang dua sigma (95%), sedangkan dalam fisika partikel, efek baru membutuhkan interval lima sigma (99.99994%) dianggap sebagai penemuan.

Latihan terpecahkan

Kelinci di Cadangan

Dalam cadangan satwa liar diperkirakan ada rata -rata 16.000 kelinci dengan standar deviasi 500 kelinci. Jika distribusi variabel 'jumlah kelinci dalam cadangan' tidak diketahui, apakah mungkin.000 dan 17.000 kelinci?

Interval dapat disajikan dalam istilah ini:

15000 = 16000 - 1000 = 16000 - 2 (500) = µ - 2 s

17000 = 16000 + 1000 = 16000 + 2 (500) = µ + 2 s

Oleh karena itu: [15000, 17000] = [µ - 2 s, µ + 2 s]

Menerapkan Teorema Tchebyshev, ada kemungkinan setidaknya 0.75 Bahwa populasi kelinci cagar alam liar adalah antara 15.000 dan 17.000 kelinci.

Rata -rata anak -anak dari suatu negara

Berat rata -rata satu anak -anak secara normal didistribusikan dengan rata -rata 10 kilogram dan standar deviasi sekitar 1 kilogram.

a) Perkirakan persentase satu anak di negara ini yang memiliki berat rata -rata antara 8 dan 12 kilogram.

8 = 10 - 2 = 10 - 2 (1) = µ - 2 detik

12 = 10 + 2 = 10 + 2 (1) = µ + 2 s

Oleh karena itu: [8, 12] = [µ - 2s, µ + 2s]

Itu dapat melayani Anda: Tukey Test: Apa yang, dalam kasus contoh, latihan terpecahkan

Menurut aturan empiris, dapat ditegaskan bahwa 68.27% anak -anak di negara ini memiliki berat antara 8 dan 12 kilogram.

b) Berapa probabilitas menemukan anak satu tahun dari 7 kilogram atau lebih sedikit berat badan?

7 = 10 - 3 = 10 - 3 (1) = µ - 3 detik

Diketahui bahwa berat 7 kilogram mewakili nilai µ - 3s, dan juga diketahui bahwa 99.73% anak -anak berada di antara 7 dan 13 kilogram berat badan. Yang hanya menyisakan 0.27% dari total anak untuk ekstrem. Setengah dari mereka, 0.135%, memiliki berat 7 kilogram atau kurang dan setengah lainnya, 0.135%, memiliki berat 11 kilogram atau lebih.

Jadi, dapat disimpulkan bahwa ada kemungkinan 0.00135 Bahwa seorang anak memiliki berat 7 kilogram atau kurang.

c) Jika populasi negara mencapai 50 juta penduduk dan anak -anak 1 tahun?

9 = 10 - 1 = µ - s

11 = 10 + 1 = µ + s

Oleh karena itu: [9, 11] = [µ - s, µ + s]

Menurut aturan empiris, 68.27% dari satu anak -satu anak dalam interval [µ -s, µ + s]

Di negara ini ada 500.000 anak satu tahun (1% dari 50 juta), jadi 341350 anak -anak (68.27% dari 500000) memiliki berat antara 9 dan 11 kilogram.

Referensi

1. Abira, v. (2002). Deviasi standar dan kesalahan standar. Majalah Semergen. Web pulih.Arsip.org.
2. Freund, r.; Wilson, w.; Mohr, d. (2010). Metode statistik. Ed ketiga. Academic Press-Elsevier Inc.
3. Alicante Server (2017). Aturan empiris (istilah statistik). Daftar Istilah pulih.Server-Alive.com.
4. Lind, d.; Marchal, w.; Wathen, s. (2012). Statistik diterapkan pada bisnis dan ekonomi. Ed kesepuluh. McGraw-Hill/Inter-American dari Meksiko. KE.
5. Salinas, h. (2010). Statistik dan probabilitas. Pulih dari UDA.Cl.
6. Sokal, r.; Rohlf, f. (2009). Pengantar Biostatistik. Ed kedua. Dover Publications, Inc.
7. Spiegel, m. (1976). Probabilitas dan statistik. Seri Schaum. McGraw-Hill/Inter-American dari Meksiko. KE.
8. Spiegel, m.; Stephens, l. (2008). Statistik. Edisi keempat. McGraw-Hill/Inter-American dari Meksiko. KE.
9. Stat119 Review (2019). Pertanyaan Aturan Pemecahan Empiris. Diperoleh dari Stat119Review.com.
10. (2019). 68-95-99.7 aturan. Diterima dari.Wikipedia.org.