Koefisien gesekan dinamis atau kinetik, contoh, latihan

Itu Gesekan dinamis atau kinetik Itu adalah salah satu yang terjadi antara dua tubuh yang bersentuhan ketika permukaan salah satu dari mereka bergerak sehubungan dengan permukaan yang lain. Misalnya, dalam kotak yang menggeser gesekan pada lereng adalah dinamis dan didistribusikan pada permukaan kontak blok.

Kecenderungan harus cukup besar, sehingga komponen tangensial berat setara atau mengatasi gaya gesekan, jika tidak blok yang turun akan berakhir berhenti.

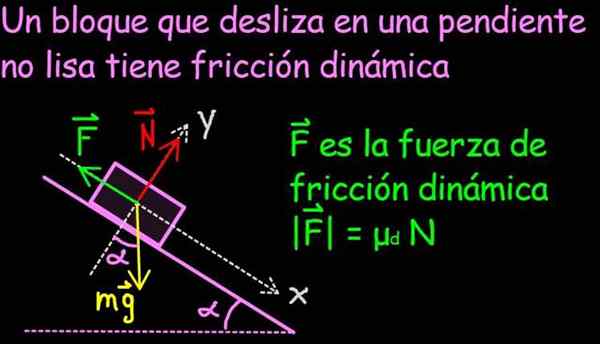Gambar 1. Gaya gesekan didistribusikan pada permukaan kontak blok, tetapi dalam diagram gaya itu direpresentasikan sebagai gaya tunggal f, sumber: f. Zapata

Kekuatan gesekan sangat penting dalam kehidupan sehari -hari, karena memungkinkan penggerak orang, hewan, dan kendaraan. Pada permukaan tanpa gesekan, seperti es krim, tidak mungkin untuk memulai gerakan.

Gesekan juga memungkinkan mobil kami berhenti begitu mereka bergerak.

Saat menerapkan rem, bantalan rem dikencangkan terhadap cakram roda dan berkat gesekan dinamis, hentikan rotasi. Tetapi tidak cukup memiliki rem yang baik, perlu ada cukup kekuatan gesekan antara ban dan lantai, karena akhirnya ini adalah kekuatan yang kami andalkan sehingga mobil berhenti.

Kemanusiaan telah belajar menangani gesekan untuk keuntungannya. Maka dimulai dengan menggunakan gesekan antara dua potong kayu kering untuk membuat api.

Alam juga telah belajar menangani gesekan yang menguntungkannya. Misalnya, membran sinovial yang menutupi tulang sendi adalah salah satu permukaan dengan koefisien gesekan terendah yang ada.

[TOC]

Koefisien gesekan dinamis

Yang pertama secara sistematis mempelajari pergerakan blok yang meluncur di permukaan datar adalah Leonardo da Vinci, tetapi studinya tidak diperhatikan.

Dapat melayani Anda: Dirac Jordan Atomic Model: Karakteristik dan Deposulat

Baru pada abad ketujuh belas fisikawan Prancis Guillaume Amonton menemukan kembali hukum gesekan:

Hukum gesekan dinamis

1.- Gaya gesekan hadir dalam blok yang meluncur di permukaan datar, selalu menentang arah gerakan.

2.- Besarnya gaya gesekan dinamis sebanding dengan keketatan atau gaya normal antara permukaan blok dan bidang pendukung.

3.- Konstanta proporsional adalah koefisien gesekan, statis μ_Dan Dalam hal tidak memiliki slip dan dinamis μ_D Saat ada. Koefisien gesekan tergantung pada bahan permukaan yang bersentuhan dan keadaan kekasaran.

4.- Kekuatan gesekan tidak tergantung pada area kontak yang jelas.

5.- Setelah pergerakan satu permukaan dimulai sehubungan dengan yang lain, gaya gesekan konstan dan tidak bergantung pada kecepatan relatif antara permukaan.

Dalam kasus ini, tidak ada gesekan geser, gesekan statis diterapkannya kurang dari atau sama dengan koefisien gesekan statis dikalikan dengan normal.

Gambar 2. Gaya gesekan dinamis menentang arah gerakan dan besarnya sebanding dengan gaya normal. Konstanta proporsionalitas adalah koefisien gesekan dinamis. Sumber: f. Zapata.

Properti terakhir adalah hasil dari kontribusi fisikawan Prancis Charles Augustin dari Coulomb, lebih dikenal karena hukum kekuatannya yang terkenal antara tuduhan listrik khusus.

Pengamatan ini membawa kita ke model matematika untuk gaya gesekan dinamis F:

F = μ_D N

Dimana μ_D Itu adalah koefisien gesekan dinamis dan N adalah gaya normal.

Bagaimana menentukan koefisien gesekan dinamis?

Koefisien gesekan dinamis antara dua permukaan ditentukan secara eksperimental. Nilainya tidak hanya tergantung pada bahan di kedua permukaan, tetapi pada keadaan kekasaran atau pemolesan yang mereka miliki, serta kebersihannya.

Dapat melayani Anda: Gelombang Mekanik: Karakteristik, Properti, Rumus, Jenis

Salah satu cara untuk menentukannya adalah dengan meningkatkan dan menggeser kotak yang dikenal pada permukaan horizontal.

Jika kecepatan diketahui pada saat digerakkan dan jarak yang ditempuh dari waktu itu diukur, dimungkinkan untuk mengetahui akselerasi pengereman karena gesekan dinamis.

Percobaan 

Dalam percobaan ini kecepatan awal diukur v dan jaraknya D, Jadi percepatan pengeremannya adalah:

A = - v² / 2d

Diagram gaya ditunjukkan pada Gambar 2. Besarnya berat adalah massa m dari blok yang dikalikan dengan percepatan gravitasi G, dan seperti yang diketahui, bobot selalu menunjuk secara vertikal ke bawah.

N Itu adalah gaya normal karena dorongan ke atas permukaan pendukung dan selalu tegak lurus (atau normal) ke bidang. Normal ada saat permukaan bersentuhan dan berhenti segera setelah permukaan dipisahkan.

Kekuatan F mewakili gaya gesekan dinamis. Ini sebenarnya didistribusikan di permukaan bawah blok, tetapi kita dapat mewakili itu sebagai satu gaya F diterapkan di tengah blok.

Karena ada keseimbangan vertikal, besarnya normal N Itu sama dengan berat mg:

N = mg

Dalam arah horizontal, gaya gesekan menghasilkan perlambatan blok massa M menurut hukum kedua Newton:

-F = m a

Kekuatan gesekan F titik ke kiri, jadi komponen horizontalnya negatif, m adalah massa blok dan A adalah akselerasi pengereman.

Sebelumnya diperoleh A = - v² / 2d Dan juga model gesekan dinamis menunjukkan bahwa:

F = μd n

Mengganti persamaan sebelumnya yang Anda miliki:

-μ_D N = - v² / 2d

Dengan mempertimbangkan bahwa n = mg, Anda sudah dapat menghapus koefisien gesekan dinamis: 

Dapat melayani Anda: model atom Schrödinger

μ_D = v² / (2d mg)

Tabel koefisien rocy dari beberapa bahan

Tabel berikut menunjukkan koefisien gesekan statis dan dinamis untuk berbagai bahan. Perlu dicatat bahwa secara sistematis koefisien gesekan statis selalu lebih besar dari koefisien gesekan dinamis.

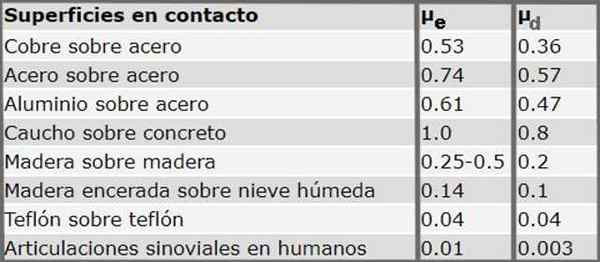Gambar 3. Koefisien gesekan statis dan dinamis untuk beberapa permukaan yang bersentuhan. Sumber: Serway R.KE. Fisik. McGraw-Hill (1992)

Latihan

- Latihan 1

Blok adonan 2 kg di lantai horizontal dipromosikan dan dilepaskan. Pada saat dirilis, kecepatan 1,5 m/s direkam. Dari saat itu hingga blok berhenti dengan gesekan dinamis 3 m. Tentukan koefisien gesekan kinetik.

Larutan

Menurut rumus yang diperoleh dalam contoh bagian sebelumnya, itu adalah koefisien dinamis (atau kinetik) adalah:

μ_D = v² / (2d mg) = 1.52 / (2x3x2 x9.8) = 0,019.

- Latihan 2

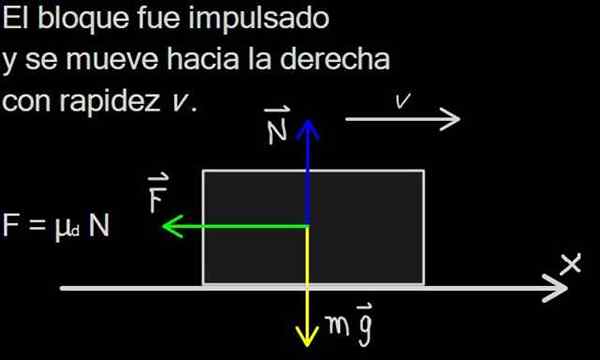
Mengetahui bahwa blok pada Gambar 1 turun dengan kecepatan konstan, bahwa massa blok adalah 1 kg dan bahwa kecenderungan bidang adalah 30º, menentukan:

a) nilai gesekan dinamis

b) Koefisien gesekan dinamis antara blok dan bidang.

Larutan

Pada Gambar 4, Persamaan Gerakan (Hukum Kedua Newton) ditunjukkan untuk masalah blok yang menurunkan kemiringan dengan koefisien gesekan μ_D  dan kecenderungan α (lihat diagram gaya pada Gambar 1)

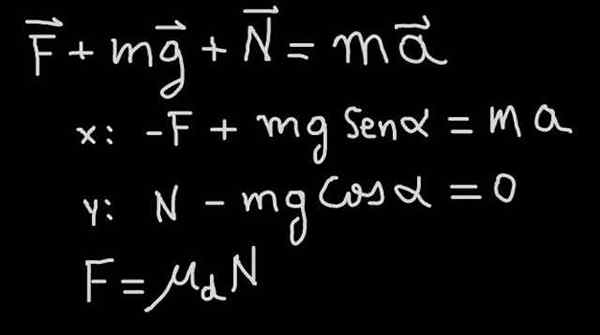Gambar 4. Hukum kedua Newton diterapkan pada blok yang meluncur di lereng dengan gesekan. Sumber: f. Zapata.

Dalam latihan kami, kami diberitahu bahwa blok turun dengan kecepatan konstan, oleh karena itu turun dengan akselerasi A = 0. Dari sana ia mengikuti bahwa gaya gesekan sedemikian rupa sehingga sama dengan komponen tangensial dari berat: f = mg sen (α).

Dalam kasus kami m = 1 kg dan α = 30º sehingga gaya gesekan f memiliki nilai 4.9n.

Di sisi lain, gaya normal N adalah sama dan bertentangan dengan komponen tegak lurus dari berat: n = mg cos (α) = 8.48n .

Dari sana ia mengikuti bahwa koefisien gesekan dinamis adalah:

μ_D = F / n = 4.9n / 8.48n = 0.57

Referensi

1. Alonso m., Finn e. 1970. Fisik. Volume I. Mekanika. Dana Pendidikan Inter -American S.KE.
2. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
3. Hewitt, hlm. 2012. Ilmu Fisik Konseptual. Edisi Kelima.
4. Rex, a. 2011. Dasar -dasar fisika. Pearson. 
5. Serway r. 1992. Fisik. McGraw-Hill.
6. Muda, h. 2015. Fisika Universitas dengan Fisika Modern. Edisi ke -14. Pearson.