Kekuatan yang dihasilkan bagaimana latihan yang dihitung dan diselesaikan

Itu memaksa hasilnya Itu adalah jumlah dari semua kekuatan yang bertindak pada tubuh yang sama. Ketika sebuah tubuh atau objek tunduk pada aksi beberapa kekuatan secara bersamaan terjadi efek. Kekuatan yang bekerja dapat digantikan oleh satu kekuatan yang menghasilkan efek yang sama. Kekuatan unik ini adalah gaya yang dihasilkan yang juga dikenal sebagai gaya bersih dan diwakili dengan simbol F_R .

Efek yang dihasilkannya F_R Itu akan tergantung pada ukuran, arah, dan artinya. Besaran fisik yang memiliki arah dan makna adalah magnitudo vektor.

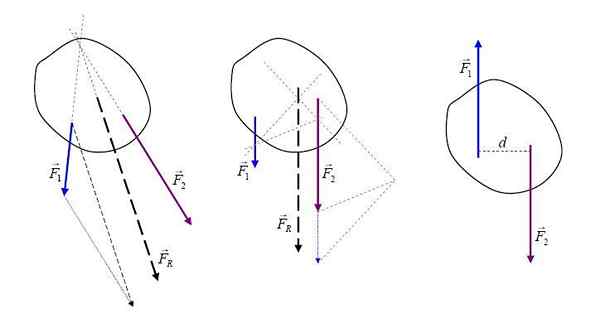Kekuatan yang dihasilkan. Oleh Ilevanat (https: // commons.Wikimedia.org/wiki/file: Rejultanta.Jpg), dari wikimedia commons

Menjadi kekuatan yang bertindak pada magnitudo tubuh dan vektor, gaya yang dihasilkan F_R  Ini adalah jumlah vektor dari semua kekuatan dan dapat diwakili secara grafis dengan panah yang menunjukkan arah dan artinya.

Dengan gaya yang dihasilkan, masalah tubuh yang dipengaruhi oleh beberapa kekuatan disederhanakan dengan menguranginya menjadi satu gaya yang bertindak.

[TOC]

Rumus

Representasi matematika dari kekuatan yang dihasilkan adalah vektor musim panas dari pasukan.

 F_R= ∑F          (1)

 ∑F = f₁+ F₂+ F₃+.. F_N           (2)

F_R= Kekuatan yang dihasilkan

∑F = Jumlah kekuatan

N= Jumlah kekuatan

Kekuatan yang dihasilkan juga dapat diwakili dengan persamaan hukum kedua Newton.

   F_R= m.ke          (3)

M= massa tubuh

a = percepatan tubuh

Jika Persamaan (1) diganti dalam Persamaan (3) Persamaan berikut diperoleh:

∑F = m.ke          (4)

F₁+ F₂+ F₃+.. F_{N =} M.ke          (5)

Ekspresi Matematika (4) dan (5) memberikan informasi tentang status tubuh dengan mendapatkan akselerasi vektor ke.

Bagaimana kekuatan yang dihitung dihitung?

Kekuatan yang dihasilkan diperoleh saat menerapkan hukum kedua Newton yang menetapkan yang berikut:

Dapat melayani Anda: kekuatan jarak

Gaya bersih yang bekerja pada tubuh sama dengan produk massa dengan percepatan yang diperolehnya. (Persamaan (3))

Percepatan tubuh akan memiliki arah gaya bersih yang diterapkan. Jika semua kekuatan yang bekerja dalam tubuh diketahui, itu akan cukup untuk menambahkannya secara vektor untuk mendapatkan gaya yang dihasilkan. Demikian juga, jika gaya yang dihasilkan diketahui maka ia akan membaginya dengan tubuh tubuh untuk mendapatkan akselerasinya.

Jika gaya yang dihasilkan dibatalkan, tubuh sedang istirahat atau kecepatan konstan. Jika gaya yang dihasilkan bekerja pada tubuh, gaya tunggal sama dengan gaya itu F_R=F.

Ketika beberapa kekuatan bertindak pada tubuh yang sama, komponen vektor gaya harus diperhitungkan, dan jika kekuatan itu paralel atau tidak.

Misalnya, jika kita secara horizontal menggeser buku yang diletakkan di atas meja. Kekuatan dalam arah horizontal adalah satu -satunya yang memberikan akselerasi pada tubuh. Gaya net vertikal pada buku ini adalah nol.

Jika gaya yang diterapkan pada buku ini memiliki kecenderungan sehubungan dengan bidang horizontal tabel, gaya ditulis berdasarkan komponen vertikal dan horizontal.

Hasilnya kekuatan paralel 

Kekuatan paralel yang bertindak pada tubuh adalah kekuatan -kekuatan yang bertindak ke arah yang sama. Mereka bisa dari dua jenis selera yang sama atau di arah yang berlawanan.

Ketika kekuatan yang bekerja pada tubuh memiliki arah yang sama dan pengertian yang sama atau berada di arah yang berlawanan, gaya yang dihasilkan diperoleh dengan melakukan jumlah aljabar dari nilai numerik gaya.

Dapat melayani Anda: Aliran medan listrik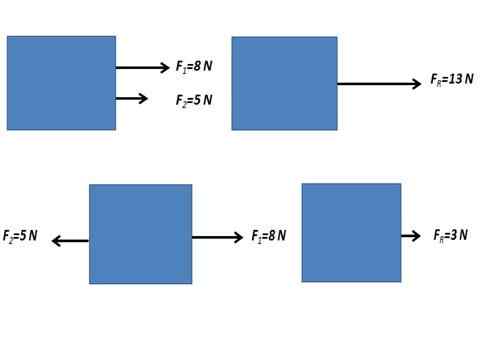Kekuatan yang dihasilkan dari dua kekuatan paralel.

Kekuatan non -paralel

Saat gaya non -paralel diterapkan pada tubuh, gaya yang dihasilkan akan memiliki komponen persegi panjang dan vertikal. Ekspresi matematika untuk menghitung gaya bersih adalah:

F_R²= (∑ f_X)²+(∑ f_Dan)²            (6)

Jadi θ_X= ∑ f_Dan / ∑ f_X         (7)

∑ f_X  dan ∑ f_X= Jumlah aljabar dari komponen X Dan Dan kekuatan yang diterapkan

θ_X= sudut yang membentuk gaya yang dihasilkan F_R Dengan poros X

Perhatikan bahwa kekuatan yang dihasilkan dari ekspresi (6) tidak disorot dalam huruf tebal dan itu karena hanya mengungkapkan nilai numerik. Alamat ditentukan oleh sudut θ_X.

Ekspresi (6) valid untuk kekuatan yang bekerja di bidang yang sama. Ketika kekuatan bertindak di luar angkasa, komponen diperhitungkan z kekuatan jika bekerja dengan komponen persegi panjang.

Latihan terpecahkan

1. Tentukan kekuatan yang dihasilkan dari tubuh yang tunduk pada kekuatan berikut yang ditunjukkan pada gambar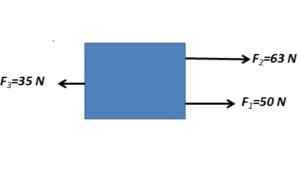

Kekuatan paralel ditambahkan dalam arti yang sama dan kurangi dengan gaya paralel di arah yang berlawanan

F_R= 63 n + 50 n - 35 n = 78n

Gaya yang dihasilkan memiliki besarnya 78N dengan arah horizontal.

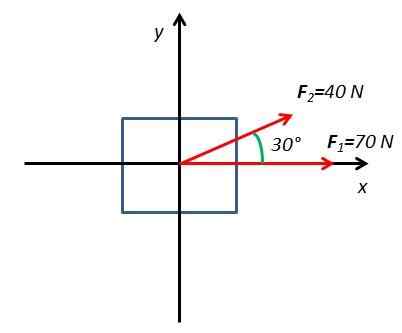
2.Hitung gaya yang dihasilkan dari tubuh di bawah pengaruh dua kekuatan F_{1 Dan} F₂. Kekuatan F₁ Ini memiliki besarnya 70N dan sedang diterapkan secara horizontal. Kekuatan F₂ Ini memiliki besarnya 40N dan sedang diterapkan pada sudut 30 ° sehubungan dengan bidang horizontal.

Untuk menyelesaikan latihan ini, diagram tubuh bebas dengan sumbu koordinat ditarik X Dan Dan

Semua komponen ditentukan X Dan Dan kekuatan yang bekerja di tubuh. Kekuatan F₁ Itu hanya memiliki komponen horizontal pada sumbu X. Kekuatan F₂ Ini memiliki dua komponen F_2x  dan f_{2 dan} yang diperoleh dari fungsi sinus dan kosinus sudut 30.

Dapat melayani Anda: gesekan: jenis, koefisien, perhitungan, latihan

F_1x = F₁=70n

F_2x = F₂ Cos 30 ° = 40 n.Cos 30 ° = 34.64n

F_1y = 0

F_{2 dan}= F₂ tanpa 30 ° = 40 tanpa 30 ° = 20n

∑ f_X =70n+34.64n = 104.64n

∑ f_Dan=20n+0 = 20n

Setelah kekuatan yang dihasilkan pada sumbu telah ditentukan X Dan Dan Nilai numerik dari gaya yang dihasilkan diperoleh.

F_R²= (∑ f_X)²+(∑ f_Dan)²

Kekuatan yang dihasilkan adalah akar kuadrat dari jumlah musim panas dari komponen kekuatan

F_R= √ (104.64n)²+(20n)²

F_R= 106.53n

Sudut yang membentuk gaya yang dihasilkan F_R Itu diperoleh dari ekspresi berikut:

θ_X= tan^-1(∑ f_Dan / ∑ f_X)

θ_X= Jadi^-1(20n / 104,64n) = 10,82 °

Kekuatan yang dihasilkan F_R Ini memiliki besarnya 106,53N dan memiliki arah yang ditentukan oleh sudut 10,82 ° yang terbentuk dengan horizontal.

Referensi

1. Dola, G, Duffy, M dan Percival, To. Fisika. Spanyol: Heinemann, 2003.
2. Avison, J H. Dunia Fisika. India: Thomas Nelson and Sons, 1989.
3. Pinent, m. Proses fisik. United Kingdom: Nelson Thomas, 2002.
4. Yadav, s k. Mekanika Teknik. Delhi: Discovery Publishing House, 2006.
5. Serway, R A dan Jewett, J W. Fisika untuk Ilmuwan dan Insinyur. California, AS: Brooks/Cole, 2010.