Matematika

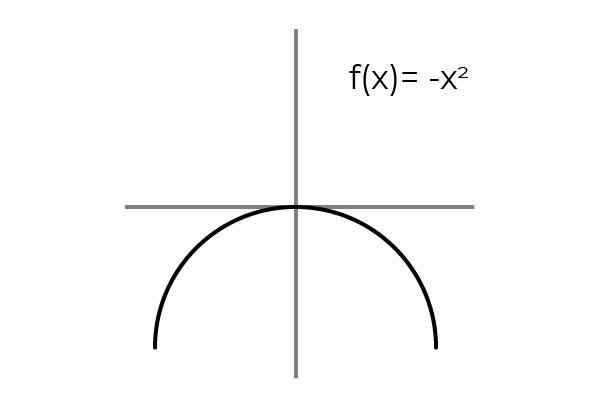
Fungsi BETTIVE APA YANG ADA, Bagaimana cara melakukannya, contoh, latihan

Fungsi BETTIVE APA YANG ADA, Bagaimana cara melakukannya, contoh, latihan

A Fungsi BYJECTIVE Itu adalah salah satu yang memenuhi kondisi ganda Suntikan dan berlebihan. Artinya, semua elemen domain memiliki satu gambar dalam kodominium, dan pada gilirannya kodominium sama dengan kisaran fungsi ( RF ).

Itu terpenuhi ketika hubungan biunivokal antara unsur -unsur domain dan kodominium dipertimbangkan. Contoh sederhana adalah fungsinya F: r → R ditentukan oleh garis F (x) = x

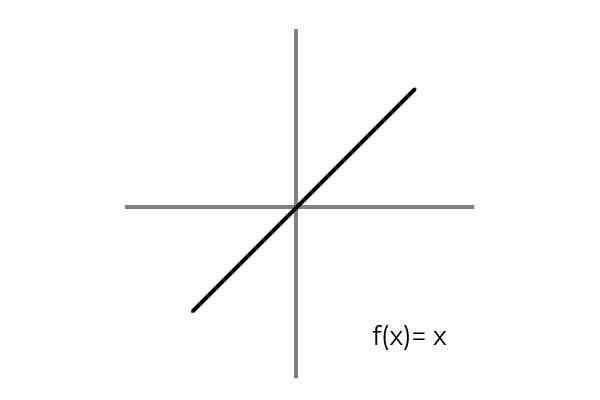Sumber: Penulis

Diamati bahwa untuk setiap nilai domain atau set keberangkatan (keduanya berlaku sama) ada satu gambar dalam kodominium atau set kedatangan. Selain itu tidak ada elemen kodominium yang bukan gambar.

Dengan demikian F: r → R ditentukan oleh garis F (x) = x

[TOC]

Bagaimana fungsi Bijyjective?

Untuk menanggapi ini, perlu memiliki konsep yang jelas terkait Injeksi Dan Overjektivitas suatu fungsi, Selain kriteria fungsi pengkondisian untuk menyesuaikannya dengan persyaratan.

Injeksi suatu fungsi

Suatu fungsi adalah Suntikan Ketika masing -masing elemen domainnya terkait dengan satu elemen kodominasi tunggal. Elemen kodominium hanya dapat menjadi gambar elemen tunggal dari domain, dengan cara ini nilai -nilai variabel dependen tidak dapat diulangi.

Mempertimbangkan Suntikan Berikut ini harus dipenuhi ke suatu fungsi:

∀ x1  ≠ x2   ⇒ f (x1 ) ≠ f (x2 )

Overjektivitas suatu fungsi

Suatu fungsi diklasifikasikan sebagai Overjective, Jika setiap elemen kodominasi adalah gambar dari setidaknya satu elemen domain.

Mempertimbangkan Overjective Berikut ini harus dipenuhi ke suatu fungsi:

Dapat melayani Anda: pengambilan sampel penggantian

Menjadi F: dF → CF

∀ B ℮ CF  DAN untuk ℮  DF   / F (a) = b

Ini adalah cara aljabar untuk menetapkan itu untuk setiap "b" yang menjadi milik cF Ada "A" milik DF sehingga fungsi yang dievaluasi dalam "A" sama dengan "B". 

Pengkondisian fungsi

Terkadang fungsi yang tidak Bytyptive, dapat menjalani pengkondisian tertentu. Kondisi baru ini dapat mengubahnya menjadi a Fungsi BYJECTIVE. Semua jenis modifikasi pada domain dan kodominasi fungsi adalah valid, di mana tujuannya adalah untuk memenuhi injeksi dan lebih dari sifat alchevity dalam hubungan yang sesuai.

Contoh: latihan terpecahkan

Latihan 1

Jadilah fungsinya F: r → R ditentukan oleh garis F (x) = 5x +1

A: [semua bilangan real]

Diamati bahwa untuk nilai domain apa pun ada gambar dalam kodominium. Gambar ini unik, yang membuat F jadilah satu Fungsi suntikan. Dengan cara yang sama kami mengamati bahwa kodominium fungsi sama dengan jangkauannya. Dengan demikian memenuhi kondisi Overjektivitas.

Menjadi suntikan dan berlebihan pada saat yang sama kita dapat menyimpulkan itu

F: r → R ditentukan oleh garis F (x) = 5x +1 adalah Fungsi BYJECTIVE.

Ini berlaku untuk semua fungsi linier (fungsi yang tingkat variabelnya lebih besar adalah satu).

Latihan 2

Jadilah fungsinya F: r → R didefinisikan oleh F (x) = 3x2 - 2

Saat menggambar garis horizontal, diamati bahwa grafik ditemukan pada lebih dari satu kesempatan. Karena ini fungsinya F Itu bukan suntikan dan karena itu tidak akan Bytyptive Saat didefinisikan R → R

Dengan cara yang sama ada nilai kodominium yang bukan gambar dari elemen domain apa pun. Karena itu, fungsinya tidak terlalu berlebihan, yang juga pantas untuk mengkondisikan set kedatangan.

Dapat melayani Anda: Teori Set: Karakteristik, Elemen, Contoh, Latihan

Domain dan kodominasi fungsi dikondisikan

                                               F: [0 , ∞] → [ - 2 , ∞ ]

Di mana diamati bahwa domain baru mencakup nilai dari nol ke infinity positif. Menghindari pengulangan nilai yang mempengaruhi suntikan.

Dengan demikian, kodominium telah dimodifikasi, menghitung dari "-2" ke infinity positif, menghilangkan dari kodominasi nilai-nilai yang tidak sesuai dengan elemen domain apa pun

Dengan cara ini dapat dipastikan itu F : [0 , ∞] → [ - 2 , ∞ ] didefinisikan oleh F (x) = 3x2 - 2

Itu bersifat bypective

Latihan 3

Jadilah fungsinya F: r → r didefinisikan oleh F (x) = sin (x)

Dalam interval [ -∞ , +∞ ] Fungsi sinus memvariasikan hasilnya antara nol dan satu.

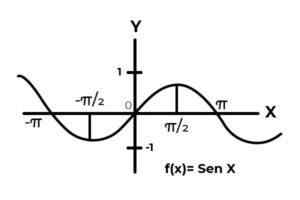Sumber: Penulis.

Fungsinya F Itu tidak sesuai dengan kriteria injektifitas dan overjectivity, karena nilai variabel dependen diulang setiap interval π. Selain itu, ketentuan kodominium di luar interval [ -sebelas ] Mereka bukan gambar dari elemen domain apa pun.

Saat mempelajari grafik fungsi F (x) = sin (x) interval diamati di mana perilaku kurva memenuhi kriteria Bubectivity. Seperti interval  DF  = [  π/2,3π/2  ] Untuk domain. DAN CF  = [-1, 1] Untuk kodominium.

Di mana fungsi bervariasi dari 1 hingga -1, tanpa mengulangi nilai apa pun dalam variabel dependen. Dan pada saat yang sama co -oominium sama dengan nilai yang diadopsi oleh ekspresi Dosa (x)

Dengan cara ini fungsinya F: [  π/2,3π/2  ] → [-1, 1]  didefinisikan oleh F (x) = sin (x). Itu bersifat bypective

Latihan 4

Naikkan kondisi yang diperlukan untuk DF dan CF. Sehingga ungkapannya

Dapat melayani Anda: Kesalahan pengambilan sampel: Rumus dan persamaan, perhitungan, contoh

F (x) = -x2  Menjadi bijeksi.

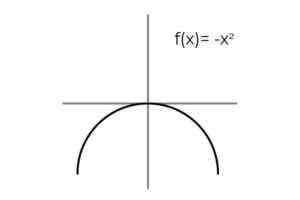Sumber: Penulis

Pengulangan hasil diamati ketika variabel mengambil nilai yang berlawanan:

F (2) = f (-2) = -4

F (3) = f (-3) = -9

F (4) = f (-4) = -16

Domain dikondisikan, membatasi ke sisi kanan garis asli.

DF = [0 , +∞ ]

Dengan cara yang sama diamati bahwa kisaran fungsi ini adalah interval [ -∞ , 0], yang, dengan melayani sebagai kodominium memenuhi kondisi overjektivitas.

Dengan cara ini kita bisa menyimpulkan itu

Ekspresi F: [0 , +∞ ] → [ -∞ , 0] didefinisikan oleh F (x) = -x2   Itu bersifat bypective

Latihan yang diusulkan

Verifikasi jika fungsi -fungsi berikut bersifat bypective:

F: [0 , ∞) → R didefinisikan oleh F (x) = 3 (x + 1)2  +2

F: [ 3π/2,5π/2  ] → R didefinisikan oleh F (x) = 5ctg (x)

F: [ -π,π  ] → R didefinisikan oleh F (x) = cos (x - 3)

F: r → R ditentukan oleh garis F (x) = -5x + 4

Referensi

  1. Pengantar logika dan pemikiran kritis. Merrilee h. Ikan salmon. Universitas Pittsburgh
  2. Masalah dalam analisis matematika. Piotr Bilar, Alfred Witkowski. Universitas Wroclaw. Tiang.
  3. Elemen analisis abstrak. Mícheál O'Searcoid PhD. Departemen Matematika. University College Dublin, Beldfield, Dublind 4
  4. Pengantar logika dan metodologi ilmu deduktif. Alfred Tarski, New York Oxford. Oxford University Press.
  5. Prinsip Analisis Matematika. Enrique Linés Escardó. Editorial Reverté s. Hingga 1991. Barcelona, ​​Spanyol.