Fungsi pertumbuhan bagaimana mengidentifikasinya, contoh, latihan

Kamu memiliki satu fungsi pertumbuhan Ketika nilai y meningkat jika x juga meningkat, yang bertentangan dengan fungsi penurunan, di mana nilai dan berkurang ketika x meningkat.

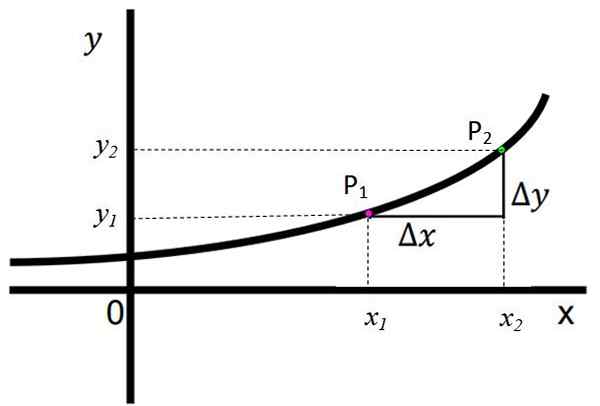
Gambar berikut menunjukkan fungsi yang tumbuh, dan diamati dengan jelas bahwa ketika bergerak dari kiri ke kanan pada sumbu x, nilai koordinat masing -masing dan, setara dengan f (x), secara bertahap meningkat. Dikatakan bahwa jika untuk semuanya x₂ > x₁, Kemudian itu ada dan₂ > dan₁.

Gambar 1. Fungsi yang berkembang. Sumber: f. Zapata.

Poin hal₁ Dan p₂ Mereka ditunjukkan, mereka masing -masing, koordinat (x₁, Dan₁) dan (x₂,Dan₂). Mereka didefinisikan:

Δy = y₂ -Dan₁

Δx = x₂ -X₁

Dalam fungsi ini, baik Δy dan Δx memiliki tanda positif, yang berarti itu dan₂ > dan₁ dan x₂ > x₁, masing -masing. Ini adalah tanda yang jelas bahwa fungsi secara efektif tumbuh.

Contoh yang baik dari fungsi yang selalu berkembang (meningkatkan monoton) adalah logaritma Neperian dari bilangan real. Semakin tinggi angkanya, semakin besar logaritma.

[TOC]

Bagaimana mengidentifikasi fungsi yang berkembang?

Dalam fungsi sederhana dan kontinu seperti yang ditunjukkan pada Gambar 1, mudah untuk menentukan apakah fungsi meningkat atau menurun, asalkan grafik tersedia.

Namun, fungsi yang lebih kompleks dapat tumbuh dalam beberapa interval dan menurun pada yang lain. Itulah mengapa kita membicarakannya Interval pertumbuhan dan berkurang dari suatu fungsi.

Di jaringan ada grafik online gratis, seperti Geogebra, yang memungkinkan grafik semua jenis fungsi. Memiliki grafik, mudah untuk menentukan apakah fungsinya selalu meningkat, seperti f (x) = log x atau jika memiliki interval di mana ia tumbuh dan lainnya di mana ia berkurang dan apa itu.

Kriteria turunan pertama

Mempertimbangkan interval numerik tertentu i, jika hasil bagi antara kuantitas Δy dan Δx positif, fungsinya meningkat. Dan sebaliknya, jika negatif, fungsinya berkurang.

Itu dapat melayani Anda: probabilitas frekuensi: konsep, bagaimana itu dihitung dan contoh

Kamu harus:

Δy / Δx> 0 → fungsi pertumbuhan

Fakta bahwa Δy / Δx> 0 dan fungsinya meningkat dalam interval tertentu, menunjukkan bahwa yang pertama berasal dari fungsi, atau lebih tepatnya tandanya, dapat digunakan sebagai kriteria untuk menentukan apakah berlaku, fungsi tersebut tumbuh secara khusus interval atau bahkan pada titik tertentu dari domain Anda.

Memang, turunan pertama didefinisikan sebagai kemiringan kurva setiap titik:

Yang berarti Δx dapat dilakukan sekecil yang Anda inginkan. Jika f '(x)> 0 untuk nilai x tertentu, misalnya x = a, kemiringan kurva pada titik itu f' (a) positif dan fungsinya akan meningkat di sana.

Teorema berikut menawarkan kriteria untuk mengetahui kapan fungsi tumbuh dalam interval (a, b):

Dalil

Misalkan f (x) menjadi fungsi yang dapat diturunkan di (a, b). Jika f '(x)> 0, untuk nilai x milik interval tersebut, dikatakan bahwa f (x) tumbuh dalam (a, b).

Teorema diterapkan untuk mencari tahu di mana interval fungsi tumbuh, mengikuti langkah -langkah ini:

Langkah 1

Temukan titik -titik di mana f '(x) = 0, serta yang di mana f' (x) tidak ada. Ini, disebut poin kritis, Ini adalah titik di mana f '(x) dapat mengubah tanda dan karenanya f (x) memiliki kesempatan untuk beralih dari tumbuh menjadi penurunan atau sebaliknya.

Langkah 2

Temukan tanda f '(x) untuk nilai sewenang -wenang di masing -masing interval yang ditentukan oleh poin yang ditemukan pada langkah 1.

Langkah 3

Gunakan teorema untuk mengetahui apakah fungsinya tumbuh atau tidak dalam setiap interval.

Contoh fungsi yang berkembang

Ada fungsi yang memiliki beberapa interval pertumbuhan dan penurunan lainnya, tetapi yang ditunjukkan di bawah ini selalu tumbuh.

Berat Badan Berdasarkan Usia

Berat orang tersebut sejak lahir, sampai kira -kira berakhir remaja, hampir selalu merupakan fungsi usia yang berkembang. Bayi dan anak -anak tumbuh dan berkembang selama bertahun -tahun, dan kemudian, ketika mereka mencapai usia dewasa, sisa hidup mereka diharapkan untuk mempertahankan bobot yang stabil, meskipun naik turunnya downs.

Dapat melayani Anda: garis vertikal

Fungsi logaritma

Fungsi logaritma variabel nyata neperian f (x) = ln x dan logaritma desimal f (x) = log x selalu tumbuh.

Fungsi akar kuadrat dari bilangan real

Fungsi lain yang selalu tumbuh adalah fungsi akar kuadrat dari bilangan real positif:

y = √x

Fungsi terkait dan fungsi linier

Fungsi terkait:

f (x) = mx + b

Itu tumbuh setiap kali garis adalah kemiringan positif. Demikian pula, identitas dan fungsi linier:

f (x) = x dan f (x) = kapak, dengan a> 0

Mereka tumbuh di semua domain mereka.

Fungsi eksponensial

Fungsi eksponensial seperti f (x) = e^X  Dan secara umum, fungsi formulir:

f (x) = a^X, Dengan> 1

Mereka tumbuh di semua domain mereka.

Fungsi indeks potensial impar

Fungsi potensial eksponen aneh, seperti ini:

• f (x) = x³
• g (x) = x⁵

Mereka selalu tumbuh.

Latihan

Latihan 1

Tentukan interval mana fungsi yang diwakili dalam grafik berikut meningkat:

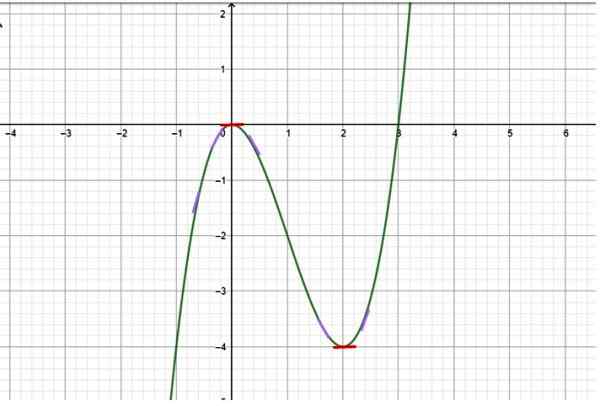Gambar 2. Fungsi dengan pertumbuhan dan penurunan interval. Sumber: f. Zapata.

Larutan

Karena grafik tersedia, dari pengamatan yang cermat, ditentukan bahwa fungsi memiliki perilaku berikut:

-Dari x → -∞ ke x = 0 fungsi meningkat, karena nilai -nilai y menjadi kurang dan kurang negatif. Segmen kemiringan kecil telah ditarik dalam warna ungu untuk menunjukkan kemiringan garis garis singgung ke kurva di berbagai titik (kemiringan garis singgung ke kurva adalah turunan pertama).

Segmen ini memiliki kemiringan positif, sehingga teorema memastikan bahwa fungsi tumbuh dalam interval ini.

-Tetapi pada x = 0 kemiringan kurva dibatalkan, yang ditunjukkan dengan segmen merah horizontal kecil. Ini adalah sebuah titik kritis dari fungsi tersebut.

Dapat melayani Anda: apa itu matematika dan untuk apa mereka? 7 aplikasi penting

Dari sana fungsi mulai berkurang, menjadi lebih negatif nilai -nilai dan. Situasi ini berlanjut hingga x = 2, yang merupakan titik kritis lainnya.

Kemudian, dalam interval dari x = 0 hingga x = 2 fungsi berkurang.

-Dari x = 2 fungsi menjadi kurang dan kurang negatif, sampai pada x = 3 melintasi sumbu x dan terus menjadi lebih positif setiap kali. Oleh karena itu ini adalah interval pertumbuhan.

Kesimpulan: Interval pertumbuhan adalah (-∞, 0) dan (2, ∞+), sedangkan interval penurunan adalah (0,2).

Latihan 2

Tentukan interval pertumbuhan dari fungsi berikut, melalui kriteria turunan pertama:

f (x) = x² - 2x

Larutan

Mengikuti langkah -langkah yang ditunjukkan di atas, turunan pertama dihitung dan sama dengan 0 untuk menemukan poin kritis:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Nilai ini menentukan keberadaan interval (-∞, 1) dan (1, ∞+). Dua nilai sewenang -wenang dipilih yang dimiliki masing -masing:

-Untuk x = 0, yang termasuk dalam (-∞, 1), Anda harus f '(0) = 2.0 - 2 = -2. Karena hasilnya negatif, fungsinya berkurang dalam interval ini.

-Untuk x = 3, milik (1, ∞+), turunan pertama bernilai f '(3) = 2.3 - 2 = 4. Karena hasilnya positif, disimpulkan bahwa fungsi tumbuh dalam interval ini.

Pembaca dapat membuat grafik fungsi asli f (x) = x² - 2x pada grafik online untuk menguatkan hasil ini.

Referensi

1. Ayres, f. 2000. Perhitungan. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Perhitungan dengan geometri analitik. Harla, s.KE.
3. Purcell, e. J., VARBERG, D., & Rigdon, s. DAN. (2007). Perhitungan. Meksiko: Pendidikan Pearson.
4. Matemobile. Fungsi, tumbuh, menurun dan konstan. Pulih dari: matemovil.com
5. Requena, b. Fungsi yang berkembang. Pulih dari: universoformulas.com.
6. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.