Mengurangi fungsi bagaimana mengidentifikasi, contoh, latihan

A fungsi penurunan f adalah orang yang nilainya menurun karena nilai x meningkat. Berarti bahwa dalam interval tertentu, mempertimbangkan dua nilai x₁ dan x₂ sedemikian rupa x₁ < x₂, lalu f (x₁)> f (x₂).

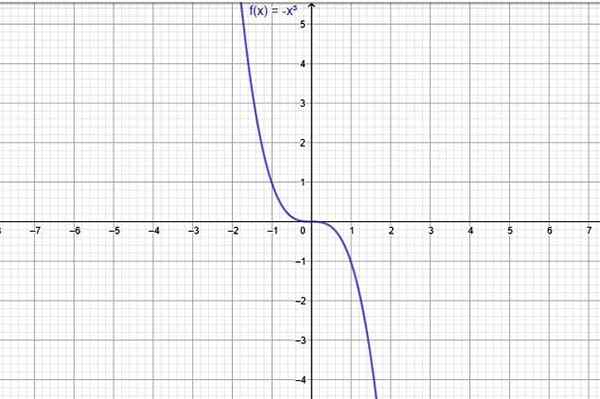
Contoh fungsi yang selalu menurun adalah f (x) = -x³, grafiknya menunjukkan gambar berikut:

Gambar 1. Fungsi yang selalu berkurang di seluruh domainnya adalah f (x) = -x^3. Sumber: f. Zapata melalui Geogebra.

Meskipun beberapa fungsi seperti ini ditandai dengan berkurang di semua domain mereka, tidak semua berperilaku seperti ini, ada peningkatan dan juga yang tumbuh dan berkurang dalam interval domain tertentu. Studi tentang pertumbuhan dan penurunan interval disebut kesamaan dari fungsi tersebut.

Demikian juga, pertumbuhan atau penurunan fungsi dapat dipertimbangkan pada titik domain tertentu. Tetapi fungsi apa pun yang menurun dalam interval tertentu, juga di setiap titik yang dimiliki olehnya.

[TOC]

Bagaimana mengidentifikasi fungsi penurunan?

Grafik fungsi menunjukkan secara visual apakah menurun atau tidak. Jika, saat bergerak dalam arti yang meningkat dari X, fungsi "turun", itu berarti menurun.

Dan jika Anda memiliki interval di mana ia berkurang dan tumbuh secara bergantian, yang paling umum, karena ini jelas diungkapkan dengan mengamati perilaku fungsi di seluruh domainnya, karena akan ada interval di mana fungsi "naik" dan lainnya di dalam "Turun" mana.

Atau, jika grafik fungsi tidak tersedia, secara analitik dimungkinkan untuk menentukan apakah menurun pada satu titik atau dalam interval, melalui turunan pertama.

Kriteria turunan pertama

Perhatikan perilaku fungsi penurunan yang ditunjukkan pada Gambar 2. Segmen garis merah muda bersinggungan dengan titik -titik yang koordinatnya adalah [a, f (a)] Dan [A+h, f (a+h)] dan memiliki kemiringan negatif.

Dapat melayani Anda: bagaimana informasi yang diperoleh dalam survei?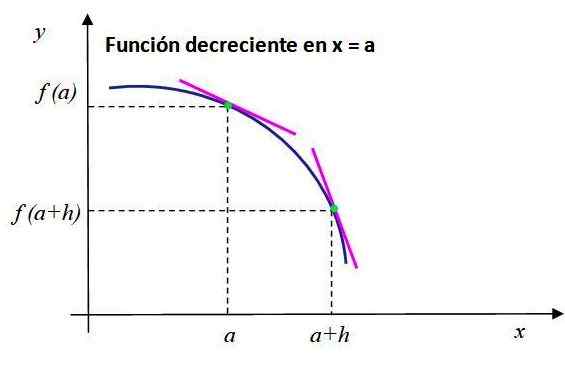Gambar 2. Kemiringan garis garis singgung ke grafik f (x) negatif pada x = a, maka fungsinya berkurang pada titik ini. Sumber: f. Zapata.

Untuk fungsi ini, berikut ini dipenuhi:

F (a+h) - f (a) < 0 ⇒  F (a+h) < f (a)

Oleh karena itu dapat dianggap bahwa fungsinya berkurang x = a.

Namun, yang pertama berasal dari fungsi f (x), dievaluasi pada x = a, yang menurut definisi adalah kemiringan garis garis singgung ke kurva pada x = a, diberikan oleh:

Batas menunjukkan bahwa nilai h dapat dilakukan sekecil yang Anda inginkan dan menyarankan bahwa tanda fa), Dapat digunakan untuk mengetahui apakah fungsi tersebut menurun pada titik tertentu, selama turunannya ada pada saat itu.

Maka ya fa) < 0, Dapat ditegaskan bahwa fungsinya menurun, dan sebaliknya, jika f '(a)> 0, Maka fungsinya tumbuh pada saat itu.

Teorema untuk mengurangi dan pertumbuhan fungsi

Sebelumnya referensi dibuat untuk perilaku fungsi pada suatu titik. Sekarang, teorema berikut memungkinkan untuk mengetahui interval di mana suatu fungsi berkurang, tumbuh atau konstan:

Biarkan F menjadi fungsi yang dapat dibedakan dalam interval (a, b). Memang benar bahwa:

-Ya f '(x) < 0 para todo x perteneciente a (a,b), entonces f(x) es decreciente en (a,b).

-Jika sebaliknya f '(x)> 0 untuk semua x milik (a, b), dikatakan bahwa fungsi f (x) tumbuh dalam (a, b).

-Akhirnya, jika f '(x) = 0 untuk semua x milik interval (a, b), f (x) konstan dalam interval tersebut.

Demonstrasi

Misalkan f '(x) < 0 para cualquier valor de x en el intervalo (a,b), además se tienen x₁ dan x₂ milik interval tersebut dan kondisi bahwa x₁< x₂.

Teorema nilai rata -rata menyatakan bahwa ada bilangan real c, antara x₁ dan x₂, seperti yang:

Dapat melayani Anda: faktor umum untuk istilah pengelompokan: contoh, latihan

Seperti yang ditetapkan sejak x₁< x₂,  Δx positif. Jadi, karena f '(c) negatif, jadi Δy juga. Karena itu f (x₁) lebih besar dari f (x₂) Dan fungsi secara efektif berkurang pada semua titik dalam interval (a, b).

Langkah -langkah untuk mengetahui apakah suatu fungsi menurun

Untuk menemukan interval penurunan dan pertumbuhan fungsi dengan menerapkan teorema sebelumnya, langkah -langkah ini diikuti:

-Temukan yang pertama berasal dari fungsi dan mencocokkannya dengan nol, menyelesaikan persamaan yang dihasilkan. Juga menentukan titik -titik di mana turunannya tidak ada.

Semua poin ini disebut poin kritis Dan perlu untuk menemukannya, karena di dalamnya turunan tersebut memiliki kesempatan untuk mengubah tanda mereka, menunjukkan bahwa fungsi berubah dari tumbuh menjadi menurun atau sebaliknya.

-Domain fungsi dibagi menjadi interval yang ditentukan oleh titik -titik di mana turunan pertama dibatalkan atau tidak ada.

-Akhirnya, tanda turunan dipelajari pada titik sewenang -wenang yang dimiliki masing -masing interval yang diperoleh pada langkah sebelumnya.

Contoh fungsi penurunan

Fungsi tidak semuanya berkurang pada tingkat yang sama, beberapa melakukannya lebih cepat dari yang lain. Fungsi -fungsi berikut, yang sering muncul dalam praktik, menurun:

Fungsi eksponensial

Fungsi bentuk f (x) = a^X, Dengan antara antara 0 dan 1, tidak termasuk ini, dengan cepat berkurang di seluruh domain mereka.

Fungsi 1/x

Melalui program grafik online sebagai geogebra, grafik fungsi f (x) = 1/x dibangun, mengkonfirmasi bahwa ia berkurang di seluruh domainnya.

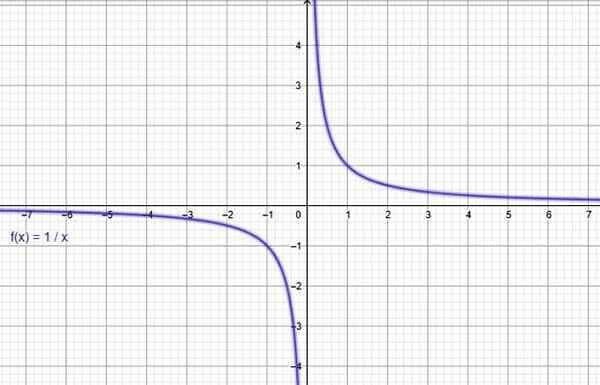Gambar 3. Fungsi f (x) = 1/x menurun. Sumber: f. Zapata melalui Geogebra.

Fungsi terkait

Fungsi bentuk y = mx + b dengan m<0 tienen gráficas que son rectas de pendiente negativa y por lo tanto son funciones decrecientes.

Dapat melayani Anda: kesetaraan matematika

Olahraga diselesaikan

Temukan, jika ada, interval penurunan fungsi:

f (x) = x⁴ - 6x² - 4

Larutan

Langkah pertama adalah menemukan f '(x):

f '(x) = 4x³ - 12x

Turunan pertama F (x) adalah fungsi kontinu, yaitu, tidak memiliki poin diskontinuitas, tetapi dibatalkan dalam:

4x³ - 12x = 0 = 4x (x²-3) = 0

Solusi dari persamaan ini adalah: x₁ = 0, x₂ = - √3 dan x₃ = √3. Ini adalah titik-titik penting, yang membagi domain f (x) dalam interval: (-∞,- √3); (- √3.0); (0, √3); (√3, ∞+).

Kemudian yang pertama diturunkan dalam nilai x sewenang -wenang dievaluasi, yang termasuk dalam setiap interval. Nilai -nilai ini dipilih:

Untuk (-∞,- √3)

F '(-2) = 4 (-2)³ - 12x (-2) = -32+24 = -8

Untuk (- √3.0)

F '(-1) = 4 (-1)³ - 12x (-1) = -4+12 = 8

Untuk (0, √3)

f '(1) = 4 (1)³ - 12x (1) = 4-12 = -8

Untuk (√3, ∞+)

f '(2) = 4 (2)³ - 12x (2) = 32-24 = 8

Seperti beberapa interval, adalah ide yang baik untuk membuat tabel untuk mengatur hasilnya. Panah ke atas menunjukkan bahwa fungsi tumbuh dan turun, yang berkurang:

Disimpulkan bahwa fungsi berkurang pada interval (-∞,- √3) dan (0, √3) dan tumbuh dalam interval yang tersisa. Fungsi asli di Geogebra mudah diperiksa dengan grafik.

Referensi

1. Ayres, f. 2000. Perhitungan. 5ed. MC Graw Hill.
2. Leithold, l. 1992. Perhitungan dengan geometri analitik. Harla, s.KE.
3. Purcell, e. J., VARBERG, D., & Rigdon, s. DAN. (2007). Perhitungan. Meksiko: Pendidikan Pearson.
4. Matemobile. Fungsi, tumbuh, menurun dan konstan. Pulih dari: matemovil.com
5. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.