Matematika

Fungsi vektor

Apa fungsi vektor?

A fungsi vektor dari parameter T, Itu adalah fungsi yang domainnya adalah nilai nyata dari T, sedangkan rute dibentuk oleh vektor formulir R (T). Fungsi seperti itu dapat dinyatakan sebagai:

R (T) = f (T) yo + G (T) J + H (T) k

Di mana yo, J Dan k Mereka adalah vektor unit dalam tiga arah utama ruang, dan fungsi f, g dan h adalah fungsi nyata dari variabel T. Notasi memanfaatkan tebal, untuk membedakan magnitudo vektor.

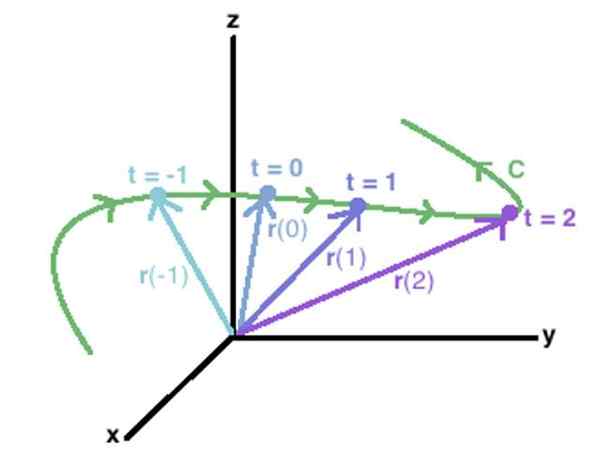Fungsi vektor dalam ruang dapat digunakan untuk menggambarkan kurva C, bergabung dengan titik -titik ekstrem dari masing -masing vektor yang ditentukan oleh fungsi tersebut. Sumber: Wikidot.

Cara lain untuk menunjukkan fungsi vektor adalah melalui kurung persegi:

R (T) = T), G (T), H (T)>

Fungsi vektor dapat digunakan untuk mempelajari kurva di bidang dan ruang, seperti lintasan yang mengikuti objek yang bergerak. Contohnya adalah perumpamaan yang dijelaskan oleh bola yang diproyeksikan dengan kecepatan awal, di bawah gravitasi.

Jika Anda ingin mengetahui posisi bola setiap saat T, Fungsi vektor dengan dua komponen, satu horizontal dan satu vertikal:

R (T) = x (T) yo + Dan(T) J

Keduanya X (T) sebagai y (T) Mereka adalah fungsi waktu T. Dengan demikian, saat bergabung dengan titik -titik ekstrem dari masing -masing vektor R(T) Mungkin, bentuk perumpamaan yang dijelaskan oleh bola di pesawat Xy.

Konsep dengan mudah meluas ke kurva C di ruang angkasa, seperti yang ditunjukkan pada gambar di atas. Vektor muncul di dalamnya R (-1), R (0), R (1) R (2), yang ujungnya menggambar kurva C, ditarik berwarna hijau.

Batas, turunan dan integral fungsi vektor

Alat perhitungan yang berlaku untuk fungsi variabel nyata nyata juga dapat diterapkan pada fungsi vektor.

Dapat melayani Anda: faktorisasi

Batas fungsi vektor

Batas fungsi vektor R (T) = f (T) yo + G (T) J + H (T) k, Saat t → A, itu didefinisikan sebagai:

$\dpi110 \displaystyle \lim_t \to a\textbfr(t)=\left [ \displaystyle \lim_ t\to a f(t)\right ]\textbfi+\left [ \displaystyle \lim_ t\to a g(t)\right ]\textbfj+\left [ \displaystyle \lim_ t\to a h(t)\right ]\textbfk$

Dengan asumsi bahwa ada batas masing -masing F (T), G (T) dan H (T), Kapan T → a.

Berasal dari fungsi vektor

Definisi berasal dari fungsi vektor R (t) = f (T) yo + G (T) J + H (T) k Itu analog dengan turunan dari fungsi nyata dari variabel nyata. Panggilan R'(t) untuk turunan tersebut, Anda memiliki:

$\dpi110 \mathbfr'(t)=\displaystyle \lim_\Delta t \to 0\frac\mathbfr(t+\Delta t)-\mathbfr(t)\Delta t$

Turunannya ada setiap kali batas sebelumnya ada, dan jika demikian, fungsinya R(T) berbeda T.

Integral fungsi vektor

Menjadi R (t) = f (T) yo + G (T) J + H (T) k fungsi vektor, sehingga fungsi f, g dan h dapat diintegrasikan T.

Jadi:

$\dpi110 \int \mathbfr(t)dt =\left [ \int f(t)dt \right ]\mathbfi+\left [ \int g(t)dt \right ]\mathbfj+\left [ \int h(t)dt \right ]\mathbfk+\mathbfC$

Dengan:

C = c₁yo + C₂J

Yang berarti bahwa konstanta integrasi juga merupakan vektor, tetapi konstan.

Contoh fungsi vektor

Contoh 1

Anda memiliki fungsi vektor yang diberikan oleh R (T) = 3sec T yo + 2tan T J. Dimungkinkan untuk mengevaluasinya untuk nilai t yang berbeda, seperti t = π/4 dan t = π, menimbulkan vektor R (π/4) dan R (π):

R (π/4) = 3SEC (π/4) yo + 2tan (π/4) J = 3√2 yo + 2 J

R (π) = 3sec (π) yo+2tan (π) J = - 3 yo

Namun, R (T) Itu tidak ada untuk nilai t = ∓π/2, ∓3π/2, ∓5π/2…, karena fungsi SEC T = 1 /cos T Itu tidak didefinisikan, begitu juga begitu T = sen T / cos T.

Oleh karena itu, domain fungsi r (t) adalah semua nilai nyata dari t, kecuali yang dari bentuk:

∓ (2n+1) π/2; Dengan n = 0, 1, 2, .. .

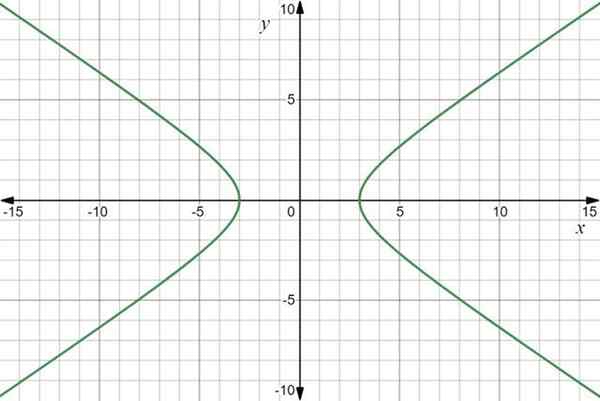
Grafik fungsi adalah hiperbola:

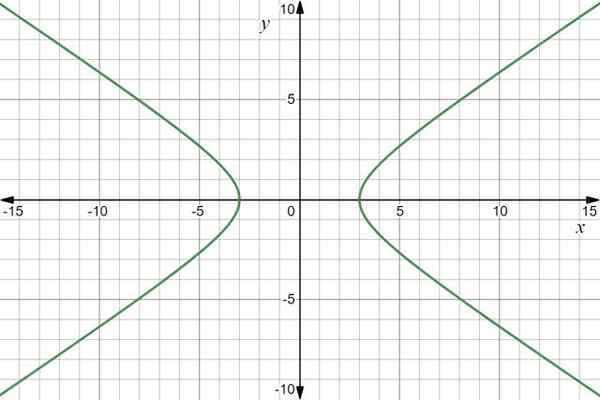Grafik fungsi vektor R (t) = 3sec t yo+2 tan t J. Sumber: f. Zapata melalui Desmos.

Contoh 2

Dalam peluncuran proyektil yang cenderung, posisi seluler adalah fungsi vektor R (T) = x (T) yo + Dan(T) J . Dengan asumsi bahwa resistensi udara tidak campur tangan, dan gravitasi adalah satu -satunya kekuatan yang bekerja pada ponsel, gerakan horizontal adalah seragam bubur, sedangkan vertikal dipercepat secara seragam, menjadi g = 9.8 m/s² Nilai akselerasi. Akselerasi ini vertikal ke arah tanah.

Dapat melayani Anda: aturan derivasi (dengan contoh)

Dalam hal ini, fungsi x (T) Dan (T) Mereka masing -masing:

x (t) = x_{salah satu} + v_sapi∙ t
dan (t) = y_{salah satu} + v_Oy∙ t - ½ gt²

Jumlah v_sapi dan v_Oy Mereka adalah komponen dari fungsi vektor yang menggambarkan kecepatan seluler setiap saat:

v (T) = v_X(T) yo + v_Dan(T) J

Dengan:

v_sapi = v_{salah satu}∙ cos θ
v_Oy = v_{salah satu}∙ sen θ

Menjadi θ sudut yang membentuk kecepatan awal sehubungan dengan horizontal.

Untuk bagiannya, posisi awal ponsel adalah titik koordinat (x_{salah satu},Dan_{salah satu}), atau setara, vektor posisi yang diberikan oleh:

R_{salah satu} (T) = x_{salah satu} yo + Dan_{salah satu} J

Perhatikan bahwa, dalam persamaan yang ditunjukkan, tanda negatif telah ditetapkan ke arah vertikal, sehingga istilah ketiga persamaan untuk y (t) mengambilnya. Juga dimungkinkan untuk menetapkan asal ke posisi awal ponsel.

Kecepatan proyektil instan

Kecepatan sesaat V (t) adalah yang pertama berasal dari posisi, sehubungan dengan waktu. Ini dihitung dengan menerapkan aturan derivasi yang diketahui:

v(t) = R ' (T) = [x (T) yo + Dan(T) J]'= X '(T) yo + Dan'(T) J = v_sapiyo + (v_Oy - GT) J

Modul kecepatan diberikan oleh:

$\dpi110 \left|\textbfv \right|=\sqrtv_ox^2+v_oy^2$

Percepatan proyektil instan

Diketahui bahwa itu adalah g, dalam arah vertikal dan arah ke bawah. Ini diverifikasi mengetahui bahwa akselerasi adalah turunan kecepatan pertama sehubungan dengan waktu (atau turunan kedua dari posisi sehubungan dengan waktu, jika lebih disukai):

ke(t) = V ' (T) = [V_sapiyo + (v_Oy - GT) J] '= [V_sapiyo] '+ [(v_Oy - GT) J] '= = - g J

Inilah hasil yang diharapkan.

Olahraga diselesaikan

Mengingat fungsi vektor R (T) = 3t yo + (T - 1) J, menemukan R '(t) dan R "(T).

Larutan

Menerapkan aturan derivasi untuk masing -masing komponen, Anda memiliki:

Dapat melayani Anda: Konstanta Integrasi: Arti, Perhitungan, dan Contoh

R '(t) = = 3 yo + J

Dan, karena turunan dari konstanta adalah 0:

R "(t) = 0

Artinya, R "(t) sama dengan vektor nol.

Referensi

Figueroa, d. 2005. Seri: Fisika untuk Sains dan Teknik. Volume 1. Kinematika. Diedit oleh Douglas Figueroa (USB).
Larson, r. Perhitungan dengan geometri analitik. 2nd. Edisi. Bukit McGraw.
Mathonline. Fungsi bernilai vektor. Dipulihkan dari: MathOnline.Wikidot.com.
Opentax. Kalkulus Volume 3. Diperoleh dari: OpenStax.org.
Purcell, e. J. 2007. Perhitungan. Pendidikan Pearson.