Sejarah latar belakang dan geometri pengembangan dari asalnya

Itu Sejarah Geometri Itu dimulai dengan peradaban pertama yang memanfaatkan cabang matematika ini secara praktis, khususnya orang -orang dari Lembah Indo dan Babel yang tahu segitiga tumpul, sekitar 3000 hingga.C.

Dalam tulisan -tulisan juru tulis Mesir Ahmes (1550 hingga.C.) Metode digunakan untuk menghitung area lingkaran. Untuk bagian mereka, orang Babilonia memiliki aturan umum untuk mengukur volume dan area. 

Ahme Papyrus atau Rhind Mathematical Papyrus

Kedua peradaban, orang Mesir dan Babel, tahu versi Teorema Pythagoras 1500 tahun sebelum versi Pythagoras. Di sisi lain, orang-orang India dari periode Veda (1500-100 hingga.C.) menggunakan geometri dalam konstruksi altar.

[TOC]

Yunani kuno

Orang -orang Yunani cenderung menuju pengembangan matematika untuk waktu yang lama. Karakter seperti Pythagoras dan Plato, terkait dengan angka dengan semua yang ada di dunia. Bagi mereka, matematika adalah kunci untuk menafsirkan alam semesta; Ideal ini diikuti dalam pengikut Pythagoras selama beberapa abad.

Tales of Miletus

Tales de Mileto adalah salah satu orang Yunani pertama yang berkontribusi pada kemajuan geometri. Waktu yang lama dihabiskan di Mesir dan dari pengetahuan dasar yang dipelajari ini. Dia adalah orang pertama yang membuat formula pengukuran geometri.

Tales of Miletus

Dia berhasil mengukur ketinggian piramida Mesir, mengukur bayangannya pada saat yang tepat di mana tingginya sama dengan ukuran bayangannya.

Pythagoras

Pythagoras

Dalam kontribusi paling signifikan dari Pythagoras (569 ke.C. - 475 a.C.) Ke geometri adalah teorema terkenal Pythagoras, yang menetapkan bahwa dalam segitiga persegi panjang, kuadrat dari hipotenus (sisi yang bertentangan dengan sudut kanan) sama dengan jumlah kotak dari sisi yang tersisa.

Elemen Euclid

Pekerjaan paling menonjol yang telah diselamatkan sejak zaman kuno telah menjadi penelitian Elemen-elemen, dari Euclid de Alejandría (325 a.C. - 265 a.C.), dibuat selama 300 -an.C. Ini adalah karya nilai historis besar yang telah berfungsi sebagai dasar untuk pengajaran matematika selama lebih dari 2000 tahun.

Euclid

Elemen-elemen Itu adalah salah satu buku pertama dan kompilasi studi yang menjelaskan prinsip -prinsip matematika yang dapat diterapkan pada situasi apa pun. Termasuk dalil, yang merupakan prinsip mendasar geometri dalam pekerjaan mereka. Di sisi lain, ada prinsip -prinsip kuantitatif yang dikenal sebagai gagasan dasar.

Pengajaran Euclid Mengurangi instrumen konstruksi dalam geometri menjadi hanya dua: aturan tanpa langkah dan kompas. Ini menghasilkan tiga masalah klasik yang tidak menemukan jawaban sampai abad kesembilan belas: quadrature of the circle, duplikasi kubus dan triseksi sudut. 

Dapat melayani Anda: di abad mana orang Spanyol menaklukkan tenochtitlan?

Bagi orang kuno, dua entitas geometris yang ideal adalah garis lurus dan lingkaran, sehingga sebagian besar teorema geometris yang diusulkan adalah produk eksplorasi dengan instrumen ini.

Geometri dalam Astronomi

Geometri juga mendapat manfaat bagi orang -orang Yunani dalam hal studi bintang -bintang. Mereka menghitung gerakan melalui pengamatan dan membuat bidang geometris langit membangun bumi sebagai titik pusat, dan baik matahari dan bulan dan planet dan entitas lainnya yang bergerak di sekitarnya, berputar di satu set lingkaran. 

Salah satu kontribusi paling berpengaruh adalah Almagest, ditulis di abad kedua d.C oleh Claudio Ptolemy (100 D. C.- 170 d.C), wadah perjanjian astronomi dari katalog bintang. Itu adalah teks paling lengkap dari masanya dan memengaruhi studi astronomi dengan cara transendental sampai Abad Pertengahan sangat maju. Itu adalah bagian dari media yang paling mempopulerkan sistem geosentris, yang mengklaim bahwa bumi adalah pusat alam semesta.

Ptoleme

Pengaruh Islam

Menjelang IX berabad -abad, ketika dunia Arab berada dalam ekspansi besar, sebagian besar budayanya meresapi beberapa bidang sains dan seni. Mereka adalah penggemar hebat karya matematika dan filosofis orang -orang Yunani. 

Salah satu cabang yang paling dieksplorasi dalam kebutuhan mereka adalah astronomi, untuk menemukan orientasi yang tepat di mana MECA adalah melakukan kalimat.

Mengikuti studi tentang Euclid dan kontribusi lain seperti Ptoleme, Muslim mengembangkan proyeksi stereografi, yaitu proyeksi bola langit di pesawat untuk menggunakannya sebagai peta. Ini berarti kemajuan mengenai studi trigonometri.

Di antara karakter yang paling representatif adalah Thābit Ibn Qurra (826/36-901) yang membuat terjemahan yang relevan dari teks-teks kuno Apollonius, Archimedes, Euclid dan Ptolemy. Beberapa di antaranya adalah satu -satunya versi yang masih hidup dari tulisan -tulisan kuno.

Eksplorasi tentang geometri astronomi juga memungkinkan penciptaan salah satu instrumen yang paling representatif, astrolabio, yang menyederhanakan perhitungan astronomi saat ini. Selain itu, instrumen ini juga memungkinkan mereka untuk mengetahui waktu dan akhirnya mendapatkan panduan ke Meca. 

Itu dapat melayani Anda: 8 kebiasaan dan tradisi Mixtec

Pengembangan Warisan Eropa

Pada abad kedua belas, setelah penyisipan ajaran klasik orang -orang Yunani berkat ekspansi Muslim dan pengembangan penemuan yang sama, terjemahan teks -teks Latin langsung dari bahasa Yunani mulai dibuat langsung dari bahasa Yunani atau dari bahasa Arab. 

Ini akan memberi jalan bagi pembelajaran baru di Eropa yang akan dipromosikan oleh Renaissance. Penemuan kembali gagasan seperti "bukti" dimulai, sebuah konsep yang dikembangkan di antara orang -orang Yunani yang tertarik pada demonstrasi postulat dalam kenyataan.

Geometri dalam Seni

Pengetahuan juga tercermin dalam seni, seperti lukisan atau arsitektur, karena geometri akan mulai menjadi bagian mendasar dari pengembangan perspektif dalam seni.

Filippo Brunelleschi (1377-1446), adalah orang yang berhasil mengembangkan perspektif linier melalui matematika. Tujuan dari teori ini adalah untuk mewakili dalam pesawat ruang tiga dimensi dari bagaimana hal itu dirasakan oleh mata manusia. Dengan demikian, ia menetapkan bahwa semua garis dalam gambar harus menyatu atau menemukan kebocoran untuk menghasilkan sensasi kedalaman. 

Filippo Brunelleschi. Sumber: i, sailko/cc by-s (http: // createveCommons.Org/lisensi/by-sa/3.0/)

Brunelleschi adalah orang pertama yang menggambarkan perspektif sebagai prosedur ilmiah dan ini berfungsi sebagai dasar pekerjaan selanjutnya dalam seni.

Dalam contoh lain dari penerapan geometri untuk studi seni dan manusia itu sendiri, adalah karya Leonardo da Vinci (1452 -1519) dalam gambarnya Pria Vitruvio. Ini adalah studi berdasarkan proporsi yang paling sempurna untuk tubuh manusia melalui analisis geometris dari strukturnya.

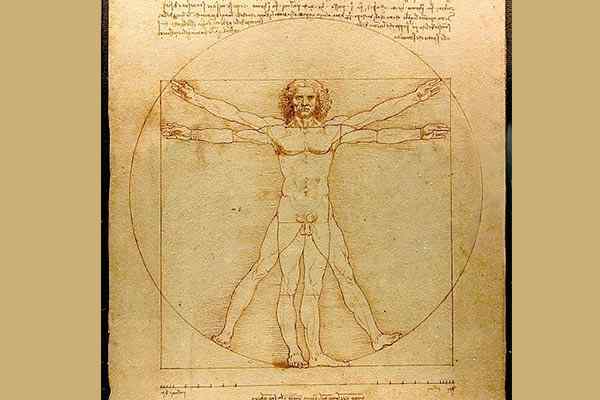The Man of Showcase oleh Leonardo da Vinci / Public Domain

Di antara area lain, arsitektur juga menonjol, di mana berbagai elemen seperti simetri dan keseimbangan mulai muncul sebagai karakteristik mendasar. Square, pintu dan jendela persegi panjang, diposisikan dengan cara yang seimbang; Penggunaan elemen klasik zaman kuno seperti kolom, kubah dan lemari besi.

Melangkah ke modernitas

Analisis perspektif dan proyeksi selama Renaissance adalah salah satu insentif untuk membangkitkan minat ahli matematika. Mulai saat ini, basis matematika yang lebih solid dan kompleks mulai didirikan dalam geometri.

Salah satu karya terpenting untuk modernitas adalah karya arsitek Girard dilucuti (1591-1661), yang dianggap sebagai awal untuk geometri proyektif. Di satu sisi, ia menetapkan bahwa garis paralel dalam proyeksi harus bertemu pada titik pada garis infinity, yaitu, cakrawala.

Dapat melayani Anda: Pemberontakan Tuxtepec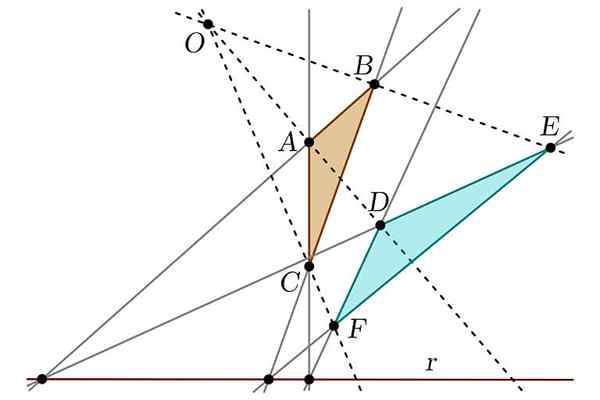Teorema yang beredar

Di sisi lain, ia juga menemukan apa yang akan diakui sebagai teorema yang beredar, yang menetapkan hubungan antara dua tokoh yang dapat dianggap "proyektif". Itu juga bertanggung jawab untuk menyederhanakan karya Apollonius sehubungan dengan bagian kerucut, membuat analogi antara sosok ini dan silinder.

Peristiwa hebat lainnya pada periode itu adalah penciptaan geometri analitik melalui studi René Descartes (1596-1650) dan Pierre de Fermat (1601-1665) secara independen. Ini adalah studi tentang geometri melalui penggunaan sistem koordinat. 

René Descartes mengerjakan desktop Anda. Wikimedia Commons

Geometri non -euclidian

Menjelang abad ke -18 dan ke -19 studi dimulai pada geometri non -euclidian. Secara khusus adalah Gauss, Johann Boleai dan Lobachevsky, yang menemukan bahwa postulat kelima Euclid, yang dikenal sebagai postulat paralel, tidak dapat diverifikasi.

Dengan cara ini mereka mengembangkan jenis geometri di mana postulat ini memenuhi syarat sebagai salah. Bentuk baru ini berhasil dengan memberikan hasil yang memuaskan dalam gaya geometri yang tidak perlu memenuhi semua postulat Euclid. Dengan demikian, geometri hiperbolik dan geometri elips lahir kemudian.

Perlu menyoroti karya Leonhard Euler (1707-1783) di abad ke-18, sehubungan dengan pengembangan notasi matematika. Selanjutnya, abad kedua puluh akan membawa serta pengembangan bidang geometri yang lebih spesifik di antaranya adalah:

-Geometri Aljabar: Ini adalah cabang matematika yang menggabungkan aljabar abstrak dan geometri analitik.

-Geometri yang terbatas: Ini adalah sistem geometris yang terdiri dari sejumlah poin yang terbatas, yaitu, mereka memiliki akhir atau batas dan oleh karena itu, mereka dapat diukur.

-Geometri Digital: Ini adalah cabang ilmu komputer yang studi tentang algoritma dan struktur data yang dapat diwakili dalam istilah geometris. 

Referensi

1. (2016) Apa yang menjadikan elemen euclid satu -satunya buku yang dapat bersaing dengan Alkitab. BBC. BBC pulih.com
2. Tiga Masalah Klasik Matematika Yunani. Universitas Antioquia. Pulih dari pengajaran.Anda.Edu.bersama
3. Heilbron J.L (2020). Geometri. Encyclopædia Britannica. Pulih dari Britannica.com
4. Sejarah Geometri. Wikipedia, ensiklopedia gratis. Diterima dari.Wikipedia.org
5. Geometri analitik. Wikipedia, ensiklopedia gratis. Diterima dari.Wikipedia.org
6. (2017) Geometri dan matematika di Renaissance. Pulih dari ukessays.com
7. Sáiz a. Perspektif Linier di Brunelleschi. Universitas Valencia. UV pulih.adalah
8. Editor Encyclopaedia Britannica (2019). Arsitektur Renaissance. Encyclopædia Britannica. Pulih dari Britannica.com
9. Andersen K (2020). Girard dilucuti. Encyclopædia Britannica. Pulih dari Britannica.com
10. (2011) Pengantar yang menarik untuk geometri komputasi. Diperoleh dari Gaussians.com