Rumus induksi magnetik, bagaimana itu dihitung dan contohnya

Itu induksi magnetik atau kepadatan fluks magnetik adalah perubahan lingkungan yang disebabkan oleh adanya arus listrik. Mereka memodifikasi sifat ruang sekitarnya, menciptakan a bidang Vektor.

Vektor Induksi magnetik, kepadatan fluks magnetik Atau sederhana Medan gaya B, Ini memiliki tiga karakteristik khas: intensitas yang diekspresikan oleh nilai numerik, alamat dan juga perasaan yang diberikan pada setiap titik dalam ruang angkasa. Itu disorot dalam huruf tebal untuk membedakannya dari jumlah numerik murni atau skalar.

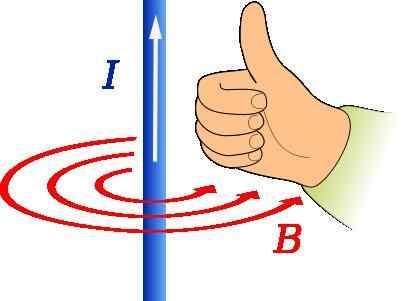Aturan ibu jari kanan untuk menentukan arah dan arah vektor induksi magnetik. Sumber: JFMelero [CC BY-SA 4.0 (https: // createveCommons.Org/lisensi/by-sa/4.0)]

Aturan ibu jari kanan digunakan untuk menemukan arah dan arah medan magnet yang berasal dari kawat yang mengangkut arus, seperti yang ditunjukkan pada gambar di atas.

Jempol tangan kanan harus menunjuk ke arah arus. Kemudian pergantian jari yang tersisa menunjukkan bentuk B, bahwa pada gambar diwakili oleh lingkaran konsentris merah.

Dalam hal ini, alamat B Itu tangensial terhadap keliling konsentris dengan kawat dan artinya bertentangan dengan tangan jam.

Itu induksi magnetik B Dalam sistem internasional Tesla (T) diukur, namun lebih umum untuk mengukurnya di unit lain yang disebut Gauss (g). Kedua unit ditunjuk masing-masing untuk menghormati Nikola Tesla (1856-1943) dan Carl Friedrich Gauss (1777-1855) untuk kontribusi luar biasa mereka terhadap ilmu listrik dan magnet.

[TOC]

Apa sifat induksi magnetik atau kepadatan fluks magnetik?

Kompas yang ditempatkan di dekat kawat dengan arus, akan selalu selaras B. Fisikawan Denmark Hans Christian Oersted (1777-1851) adalah orang pertama yang menyadari fenomena ini pada awal abad ke-19.

Dapat melayani Anda: kecepatan areolar: bagaimana latihan itu dihitung dan diselesaikan

Dan ketika saat ini berhenti, kompas menunjuk ke utara geografis, seperti biasa. Dengan mengubah posisi kompas dengan hati -hati, peta diperoleh dari bentuk medan magnet.

Peta ini selalu memiliki bentuk lingkaran konsentris ke kawat, seperti yang dijelaskan di awal. Dengan cara ini dapat divisualisasikan B.

Bahkan jika kawatnya tidak lurus, vektor B akan membentuk lingkaran konsentris di sekitarnya. Untuk menentukan bentuk apa yang dimiliki lapangan, sudah cukup untuk membayangkan segmen kawat yang sangat kecil, sangat kecil sehingga mereka tampak bujursangkar dan dikelilingi oleh keliling konsentris.

Garis medan magnet diproduksi oleh loop kawat yang mengangkut arus. Sumber: Pixabay.com

Ini menunjukkan sifat penting dari garis medan magnet B: Mereka kurang prinsip atau akhir, mereka selalu kurva tertutup.

Hukum Biot-Savart

Abad ke -19 menentukan awal era listrik dan magnet dalam sains. Menjelang tahun 1820 fisikawan Prancis Jean Marie Biot (1774-1862) dan Felix Savart (1791-1841) menemukan hukum yang menyandang namanya dan yang memungkinkan menghitung vektor B.

Mereka membuat pengamatan berikut tentang kontribusi pada medan magnet yang dihasilkan oleh segmen kawat panjang diferensial dl yang mengangkut arus listrik yo:

• Besarnya B berkurang dengan terbalik ke kuadrat jarak ke kawat (ini masuk akal: jauh dari kawat intensitas B Itu pasti kurang dari di titik terdekat).
• Besarnya B Itu sebanding dengan intensitas arus yo yang melakukan perjalanan di kawat.
• Alamat B Itu tangensial untuk lingkar radio R berpusat di kawat dan arah B Itu diberikan, seperti yang kami katakan, dengan aturan ibu jari yang tepat.

Produk vektor atau produk silang adalah alat matematika yang sesuai untuk mengekspresikan poin terakhir. Untuk membangun produk vektor, dua vektor diperlukan, yang didefinisikan sebagai berikut:

• Dl Itu adalah vektor yang besarnya adalah panjang segmen diferensial dl
• R Itu adalah vektor yang beralih dari kawat ke titik di mana Anda ingin menemukan lapangan

Dapat melayani Anda: spektrum elektromagnetik: karakteristik, pita, aplikasi

Rumus

Semua ini dapat digabungkan dalam ekspresi matematika:

Konstanta proporsionalitas yang diperlukan untuk menetapkan kesetaraan adalah Permeabilitas magnetik ruang kosong μ_{salah satu}  = 4π.10^-7 T.m/a

Ekspresi ini adalah Hukum Biot dan Savart, yang memungkinkan Anda menghitung medan magnet dari segmen saat ini.

Segmen tersebut pada gilirannya harus menjadi bagian dari sirkuit yang lebih besar dan lebih besar: distribusi saat ini.

Kondisi bahwa sirkuit ditutup diperlukan agar arus listrik mengalir. Arus listrik tidak dapat mengalir di sirkuit terbuka.

Akhirnya, untuk menemukan medan magnet total dari distribusi saat ini, semua kontribusi dari setiap segmen diferensial ditambahkan Dl. Ini setara dengan mengintegrasikan semua distribusi:

Untuk menerapkan hukum Biot-Savart dan menghitung vektor induksi magnetik, perlu untuk mempertimbangkan poin-poin penting yang sangat penting:

• Produk vektor antara dua vektor selalu menghasilkan vektor lain.
• Besarnya produk vektor dalam undang-undang Biot-Savart adalah:Di mana θ adalah sudut antara Dl Dan R.
• Produk vektor harus ditemukan sebelum Jika resolusi integral diselesaikan, maka integral dari masing -masing komponen yang diperoleh secara terpisah diselesaikan.
• Perlu untuk menarik situasi dan membangun sistem koordinat yang memadai.
• Setiap kali keberadaan beberapa simetri diamati, itu harus digunakan untuk menghemat waktu perhitungan.
• Ketika ada segitiga, teorema Pythagoras dan teorema kosinus sangat membantu untuk membangun hubungan geometris antara variabel.

Bagaimana itu dihitung?

Dengan contoh praktis dari perhitungan B Untuk kawat bujursangkar, rekomendasi ini diterapkan.

Itu dapat melayani Anda: beban tepat waktu: Properti dan Hukum Coulomb

Contoh

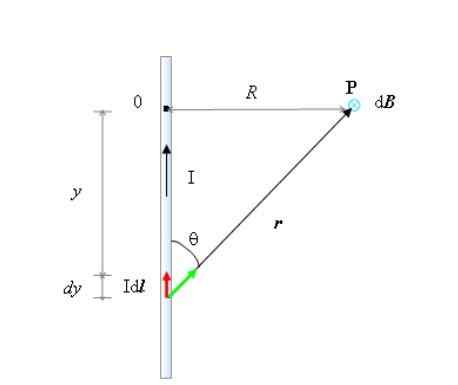
Hitung vektor medan magnet yang dihasilkan oleh kawat bujursangkar yang sangat panjang pada titik p ruang, menurut gambar yang ditunjukkan.

Geometri yang diperlukan untuk menghitung medan magnet pada titik P, dari kawat arus yang sangat panjang. Sumber: Made sendiri.

Dari sosok yang harus Anda lakukan:

• Kawat diarahkan secara vertikal, dengan arus saya mengalir. Alamat ini adalah +dan dalam sistem koordinat, yang asalnya tepat atau.
• θ adalah sudut antara Dl Dan R Dan juga benar bahwa: 
• Dalam hal ini, menurut aturan ibu jari kanan, B Pada titik P diarahkan di koran, sehingga dilambangkan dengan lingkaran kecil dan "x" pada gambar. Alamat ini akan diambil sebagai -z.
• Segitiga kanan yang kakinya Dan Dan R, menghubungkan kedua variabel menurut teorema Pythagoras: R²= R²+Dan²

Semua ini diganti dalam integral. Vektor atau produk silang ditunjukkan oleh besarnya arah plus dan maknanya:

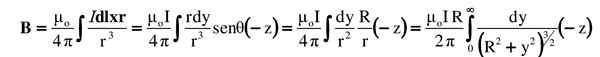
Integral yang diusulkan dicari dalam tabel integral atau diselesaikan dengan substitusi trigonometri yang tepat (pembaca dapat memeriksa hasilnya menggunakan y = rtg θ):

Hasilnya setuju dengan yang diharapkan: besarnya bidang berkurang dengan jarak r dan meningkat secara proporsional dengan intensitas arus i.

Sementara kawat yang sangat panjang adalah idealisasi, ekspresi yang diperoleh adalah pendekatan yang sangat baik untuk bidang kawat panjang.

Dengan Hukum Biot dan Savart adalah mungkin untuk menemukan medan magnet dari distribusi simetri tinggi lainnya, seperti spiral melingkar yang mengangkut arus, atau kabel terlipat yang menggabungkan segmen bujursangkar dan lengkung.

Tentu saja, untuk menganalisis yang integral, masalahnya harus memiliki tingkat simetri yang tinggi. Kalau tidak, alternatifnya secara numerik memecahkan integral.

Referensi

1. Serway, r., Jewett, J. (2008). Fisika untuk Sains dan Teknik. Volume 2. Meksiko. Editor Pembelajaran Cengage. 367-372.