Matematika

Interpolasi linier

2751
767
Miss Wm Hudson

Kami menjelaskan apa interpoasi linier, formulasinya, bagaimana melakukannya, dengan contoh dan latihan diselesaikan

Apa interpolasi linier?

Itu Interpolasi linier Ini terdiri dari memperkirakan lokasi titik dalam interval numerik, dengan asumsi bahwa nilai -nilai ekstrem interval tersebut disatukan oleh garis. Diketahui persamaan garis ini, dimungkinkan untuk menemukan titik yang tidak diketahui.

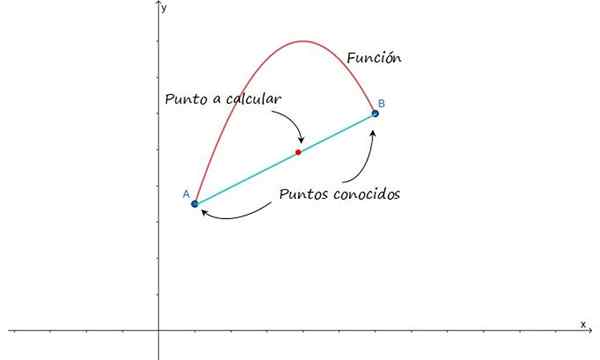
Idenya direkema pada gambar berikut, yang menunjukkan pendekatan pada grafik fungsi antara titik A dan B. Dengan asumsi bahwa titik -titik ini dekat, dimungkinkan untuk memperkirakan kurva yang menyatukannya melalui garis dan dengan demikian menemukan titik -titik perantara.

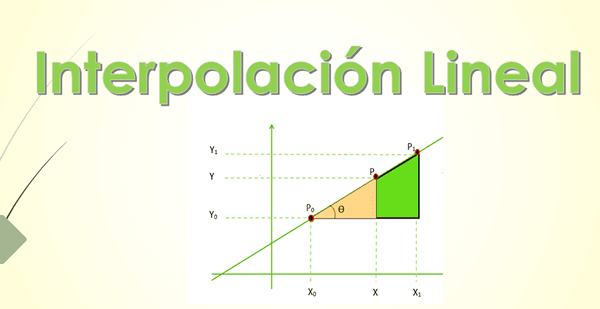
Gambar 1.- Untuk membuat interpolasi linier antara titik A dan B harus diasumsikan bahwa mereka disatukan oleh garis . Sumber: f. Zapata.

Anda juga dapat memperkirakan kurva yang bergabung dengan titik yang diberikan dengan menggunakan fungsi kuadratik atau polinomial lainnya. Namun, garis ini memiliki keuntungan dari kesederhanaan matematika, sehingga mudah ditangani, meskipun menjadi interpolasi paling sederhana dari semuanya, ada kemungkinan bahwa hasilnya tidak setepat yang diperoleh dengan menggunakan fungsi lain.

Rumus

Ada dua poin koordinat [x_{salah satu}, f (x_{salah satu})] dan [x₁, f (x₁)] di antaranya adalah titik [x, g (x)], yang koordinatnya diinginkan untuk mengetahui.

Langkah pertama terdiri dari bergabung dengan titik yang diketahui melalui segmen garis, di mana koordinat titik penghitungan ditemukan.

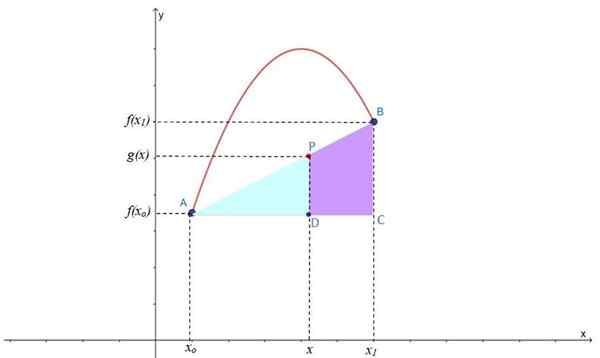Gambar 2.- Interpolasi linier untuk menemukan titik p pada garis interpoching g (x), terletak di antara titik A dan B dari f (x). Sumber: f. Zapata.

Seperti yang Anda lihat, dua persegi panjang terbentuk: ABC dan APD, yang juga memiliki sudut pandang akut yang sama, sehingga mereka adalah segitiga yang sama, yang dapat diterapkan oleh teorema Thales:

Itu dapat melayani Anda: geometri analitik

$\fracADAC=\fracAPAB=\fracPDBC$ Mengganti ukuran segmen sesuai dengan grafik, hubungan berikut diperoleh:

$\fracx-x_ox_1-x_o=\fracg(x)-f(x_o)f(x_1)-f(x_o)$ Dari sana kami melanjutkan untuk menghapus g (x):

$g(x)=f(x_o)+\left [\fracf(x_1)-f(x_o)x_1-x_o \right ]\left ( x-x_o \right )$ Panggilan:

F₁(X₁) = y₁ ; F_{salah satu}(X_{salah satu}) = y_{salah satu}; g (x) = y

Persamaan teratas diubah menjadi:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Rentang kesalahan

Ketika suatu fungsi mendekati dengan metode ini, tingkat kesalahan diberikan oleh nilai absolut dari perbedaan antara fungsi f (x) dan jalur interpolasi G (x):

Kesalahan = │f (x) - g (x) │

Cara membuat interpolasi linier?

Melakukan interpolasi linier sangat sederhana, Anda hanya perlu mengikuti langkah -langkah ini:

Langkah 1

Tentukan titik p (x, y) yang tidak diketahui.

Langkah 2

Menetapkan dua titik yang membatasi interval di mana nilai yang akan dihitung berada, yaitu, titik (x x_{salah satu},Dan_{salah satu}) dan (x₁, Dan₁).

Langkah 3

Ganti semua nilai dalam persamaan:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

Dan menghitung hasilnya.

Contoh interpolasi linier

Contoh 1

Anda ingin menemukan nilai perkiraan LN 3 melalui interpolasi linier, mengingat nilai -nilai berikut:

Ln 2 = 0.693147 dan ln 4 = 1.386294

Bandingkan hasilnya dengan nilai LN 3 yang diperoleh melalui kalkulator dan tentukan margin yang dilakukan.

Langkah 1

Untuk menemukan nilai perkiraan LN 3 Anda harus melanjutkan cara berikut: Pertama, yang tidak diketahui ditetapkan, yaitu y = ln 3, di samping nilai yang sesuai dari "x": x = 3. Inilah titik yang ingin Anda hitung: (3, ln 3).

Langkah 2

Maka Anda harus menetapkan titik batas interval dengan nilai yang diketahui. Itu diminta untuk melakukannya dengan beberapa poin berikutnya:

Batas bawah: [x_{salah satu} = 2; Dan_{salah satu} = ln 2 = 0.693147]
Batas atas: [x₁ = 4; Dan₁ = ln 4 = 1.386294]
Langkah 3

Nilai yang ditentukan dalam Langkah 1 dan 2 diganti dengan cermat dalam persamaan untuk menghasilkan hasil dari pendekatan ke LN 3:

Dapat melayani Anda: berapa banyak solusi yang dimiliki persamaan kuadratik?

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln\: 2+\left [\fracln4-ln24-2 \right ]\left (3-2 \right )$
$ln\: 3= 0.693147+\left [\frac1.386294-0.6931474-2 \right ]\left (3-2 \right )=1.039721$ Nilai riil LN 3 yang diperoleh dengan kalkulator adalah:

Ln 3 = 1.098612

Dan margin kesalahan adalah:

Kesalahan = │1.098612 - 1.03971 │ = 0.059

Persentase kesalahan interpolasi dihitung dengan membagi kesalahan antara nilai riil LN3 dan pengalikan dengan 100 %:

Persentase kesalahan = (kesalahan/nilai nyata) × 100 = (0.059/1.098612) × 100% = 5.4%

Contoh 2

Sekarang Anda ingin menemukan nilai perkiraan LN 3 dengan interpolasi linier, diketahui dua nilai ini:

Ln 2.5 = 0.916291 dan ln 3.5 = 1.252763

Juga menentukan kesalahan yang sesuai dan bandingkan dengan hasil dari contoh sebelumnya.

Langkah 1

Sekali lagi poin yang tidak diketahui adalah:

y = ln 3, x = 3

Langkah 2
Batas bawah: [x_{salah satu} = 2.5; Dan_{salah satu} = y_{salah satu} = Ln 2.5 = 0.916291]
Batas atas: [x₁ = 3.5; Dan₁ = Ln 3.5 = 1.252763]
Langkah 3

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$ln\: 3= ln \: 2.5+\left [\fracln\: 3.5-ln \: 2.53.5-2.5 \right ]\left (3-2.5 \right )=1.084527$ Memeriksa nilai yang ditawarkan oleh kalkulator:

Ln 3 = 1.098612

Level kesalahan ditentukan dalam kasus ini, yang hasilnya:

Kesalahan = │1.098612 - 1.084527 │ = 0.014

Kesalahan persentase dalam kasus ini adalah ≈ 1.3 %. Dibandingkan dengan tingkat kesalahan Contoh 1, nilai baru lebih tepat, karena interval yang dipilih untuk interpolar lebih rendah.

Latihan terpecahkan

Latihan 1

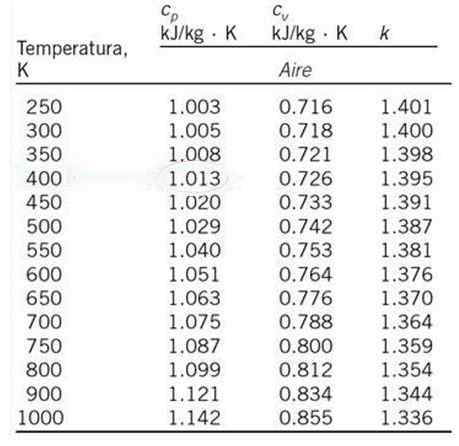
Hitung, dengan interpolasi linier, panas spesifik udara pada tekanan konstan c_P dan suhu 530 K, mulai dari tabel nilai yang ditunjukkan di bawah ini.

Larutan

Dalam resolusi banyak masalah, adalah umum bahwa nilai yang dicari tidak tampak persis seperti yang diinginkan dalam tabel nilai yang ada. Alternatifnya adalah memilih nilai yang paling dekat dengan yang diinginkan, tetapi berkali -kali interpolasi linier sudah cukup untuk menemukan pendekatan yang jauh lebih baik.

Dapat melayani Anda: tanda -tanda pengelompokan

Nilai c_P 530 K tidak muncul di tabel yang terpasang, tetapi interpolasi linier dapat dibuat dengan masing -masing pemanasan spesifik pada 500 K dan 550 K, yang merupakan suhu yang paling dekat dengan 530 K dan yang pemanasan spesifiknya muncul dalam tabel yang ditunjukkan.

Panas spesifik masing -masing panas untuk suhu ini adalah:

T_{salah satu} = 500 K; C_PO = 1.029 kJ /kg ∙ k

T₁ = 550 K; C_P1 = 1.040 kJ /kg ∙ k

Dan yang tidak diketahui adalah intinya (500k, c_P)

Mengganti dalam rumus interpolasi linier yang diberikan di atas, dengan t pada adegan variabel "x" dan c_P Alih -alih "Y", Anda memiliki:

$y=y_o+\left [\fracy_1-y_ox_1-x_o \right ]\left (x-x_o \right )$

$c_p= c_po+\left [\fracc_p1-c_poT_1-T_o \right ]\left (T-T_o \right )$

$c_p= 1.029+\left [\frac1.040-1.029550-500 \right ]\left (530-500 \right )\frackJkg\cdot K=1.03536\frackJkg\cdot K$

Latihan 2

Beban yang diterapkan pada pegas (dalam kilopondios) menghasilkan perpanjangan berikut (dalam milimeter) sesuai dengan tabel yang ditunjukkan:

Hitung perpanjangan saat beban 12.6 kp.

Larutan

Biarkan dan nilai perpanjangan yang dicari saat beban adalah C = 12.6 kp. Titik yang tidak diketahui adalah (12.6, y), yang merupakan salah satu poin:

C_{salah satu} = 10 kp; Dan_{salah satu} = 105 mm

C₁ = 15 kp; Dan₁ = 172 mm

Hanya tetap menggantikan nilai dalam persamaan:

$C= 105+\left [\frac172-10515-10 \right ]\left (12.6-10 \right )\: mm=139.84\: mm$ Latihan yang diusulkan

Hitung panas panas spesifik hingga volume konstan untuk suhu 727 K, menggunakan interpolasi linier dan tabel sekuritas latihan diselesaikan 1.

Referensi

Akademi Rafa Vilchez. Bagaimana melakukan interpolasi linier. Dipulihkan dari: Academiraafavilchez.com
Chapra, s. 2007. Metode numerik untuk insinyur. Ke -5. Edisi. Bukit McGraw.
Akademi Khan. Matematika interpolasi linier. Pulih dari: Khanacademy.org.
Kehidupan pendidikan. Formula interpolasi linier. Dipulihkan dari: TheeducationLife.com
X-Engineer. Interpolasi linier dan ekstrapolasi dengan kalkulator. Pulih dari: X-engineer.org.

Interpolasi linier

Apa interpolasi linier?

Rumus

Rentang kesalahan