Formula Hukum Biot-Savart, Demonstrasi, Aplikasi, Latihan

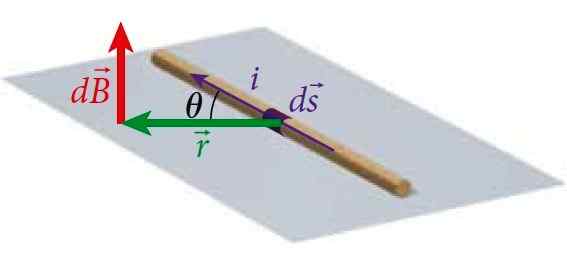
Itu Hukum Biot-Savart membangun hubungan antara medan magnet DB  Pada titik P, diproduksi oleh kawat tipis yang mengangkut I saat ini dan yang panjang diferensialnya adalah DS. Undang -undang ini digunakan untuk menemukan medan magnet distribusi saat ini melalui Prinsip superposisi. 

Ini berarti bahwa untuk menghitung medan magnet total pada titik P, kita harus menambahkan semua kontribusi bahwa setiap bagian diferensial DS dari kawat berkontribusi. Dan jumlah ini dilakukan melalui integral yang dilakukan selama seluruh distribusi saat ini.

Gambar 1. Segmen kawat mengangkut I arus, yang menghasilkan medan magnet pada titik p pada jarak tertentu dari kawat, yang dihitung oleh hukum biot-savart. Sumber: Bauer, W. Fisika untuk Teknik dan Ilmu Pengetahuan.

Dengan cara ini Anda dapat menghitung bidang yang menghasilkan kabel dengan arus geometri yang berbeda.

Hukum Biot-Savart dinamai menurut dua fisikawan Prancis yang menemukannya pada tahun 1820: Jean Marie Biot (1774-1862) dan Felix Savart (1791-1841). Untuk mencapai hal ini, mereka harus mempelajari intensitas dan bentuk medan magnet yang dihasilkan oleh berbagai distribusi saat ini.

[TOC]

Rumus

Ekspresi matematika dari undang-undang Biot-Savart adalah sebagai berikut:

Ini mempertahankan analogi dengan setara untuk menghitung medan listrik: Hukum Coulomb, hanya bahwa medan magnet DB di P IS tegak lurus ke pesawat tempat kawat berada. Kita bisa melihat ini pada Gambar 1.

Ekspresi sebelumnya juga dapat ditulis sebagai berikut:

Dalam kedua ekspresi, R Ini adalah vektor posisi, diarahkan dari elemen saat iniS Ke titik di mana Anda ingin menghitung bidang.

Dapat melayani Anda: konservasi momentum linier: prinsip, contoh, latihan.

Untuk bagian ini, R Dengan aksen sirkumflejo itu adalah vektor kesatuan yang diarahkan ke arah dan arah yang sama, tetapi dengan modul yang sama dengan 1. Vektor R Itu diwakili sebagai berikut:

Untuk alasan ini, dengan mengganti persamaan sebelumnya -yang memiliki r³ Dalam penyebut- ekspresi r segera tercapai² Di Denominator.

Selain vektor yang disebutkan di atas, rumus ini mengandung μ_{salah satu}, panggilan Permeabilitas vakum dan nilainya yang:

μ_{salah satu} = 4π x10^-7 T.m/ a.

Jika kita ingin menghitung vektor medan magnet, perlu untuk mengintegrasikan semua distribusi saat ini, di mana kita memerlukan data tentang geometri:

Produk vektor dan aturan tangan kanan

Undang-undang Biot-Savart melibatkan produk vektor antara vektor IDS Dan R. Hasil dari produk vektor antara dua vektor juga merupakan vektor.

Dalam hal ini modul produk ID VectorS X R IS: (IDS) ⋅R⋅senθ, di mana θ adalah sudut antara idS Dan R, seperti yang ditunjukkan pada Gambar 1.

Dengan cara ini besarnya bidang DB Itu diberikan oleh:

Arah dan makna dapat ditentukan dengan aturan tangan kanan, yang diilustrasikan dalam gambar ini:

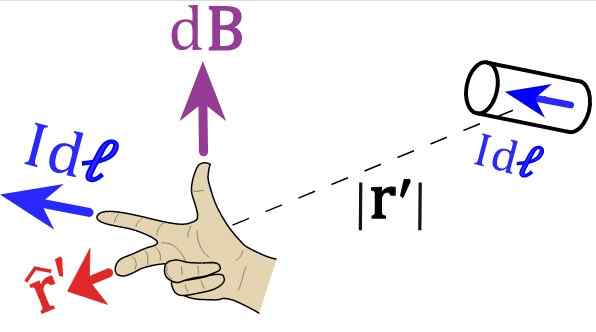Gambar 2. Aturan Tangan Kanan untuk Hukum Biot-Savart. Sumber: Wikimedia Commons.

Kami mengundang pembaca untuk memposisikan tangan kanannya mengikuti vektor Gambar 1 dan 2. Untuk Gambar 1, jari telunjuk harus menunjuk ke kiri, mengikuti IDS atau idl, Titik Jari Tengah sesuai dengan vektor R kesatuan.

Dan akhirnya ibu jari diarahkan ke atas dan ini adalah arah medan magnet.

Dapat melayani Anda: ellipsoid: karakteristik dan contoh

Demonstrasi Hukum Biot-Savart

Hukum Biot-Savart sangat eksperimental, yang berarti bahwa formulasinya berasal dari banyak pengamatan tentang perilaku medan magnet yang dihasilkan oleh kabel saat ini.

Pengamatan Biot dan Savart

Ini adalah pengamatan para ilmuwan Prancis tentang medan magnet DB:

-Besarnya DB berbanding terbalik dengan R².

-Ini juga berbanding lurus dengan besarnya elemen saat ini, yang disebut idS Dan juga ke sen θ, di mana θ adalah sudut antara vektor dS Dan R.

-DB tegak lurus terhadap kedua idS -arah saat ini- R.

-Beragam dB adalah tangensial ke lingkaran radio R kawat -centir. Dengan kata lain, bidang B yang diproduksi oleh segmen saat ini terdiri dari keliling konsentris terhadap tandus.

-Makna di mana ia berputar B Itu diberikan oleh aturan ibu jari kanan: ibu jari kanan diarahkan ke arah arus dan empat jari yang tersisa melengkung di sekitar kawat, mengikuti sirkulasi lapangan.

Semua pengamatan ini digabungkan dalam ekspresi matematika hukum yang dijelaskan sebelumnya.

Aplikasi Hukum Biot-Savart

Ketika distribusi saat ini memiliki simetri tinggi, integral dapat dengan mudah diselesaikan, mari kita lihat beberapa kasus:

Kawat bujursangkar dan tipis

Kawat bujursangkar dengan panjang L mengangkut I saat ini, seperti yang muncul pada gambar.

Itu menggambarkan geometri yang diperlukan untuk perhitungan bidang. Ini tegak lurus terhadap selembar kertas, keluar ke pesawat jika arus mengalir dari kiri ke kanan, dan masuk yang masuk (periksa dengan aturan kanan).

Dapat melayani Anda: paramagnetisme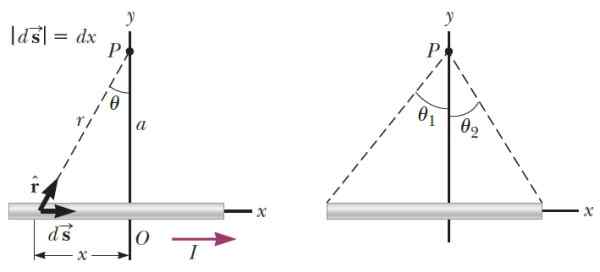Gambar 3.- Di sebelah kiri geometri yang diperlukan untuk menghitung medan magnet yang menghasilkan segmen kawat tipis pada titik p. Di sebelah kanan sudut yang menentukan posisi P sehubungan dengan ujung segmen. Sumber: Serway, R. Fisika untuk Sains dan Teknik.

Menjadi k  Vektor unit dalam arah tegak lurus terhadap bidang, setelah melakukan proses pengintegrasian, medan magnet yang dihasilkan kawat dalam P adalah:

Spira melingkar

Loop melingkar radio ke Itu mengangkut arus seperti yang ditunjukkan pada gambar dan menghasilkan medan magnet DB -dalam warna hijau gelap pada p pada sumbu aksial, pada jarak X dari tengah.

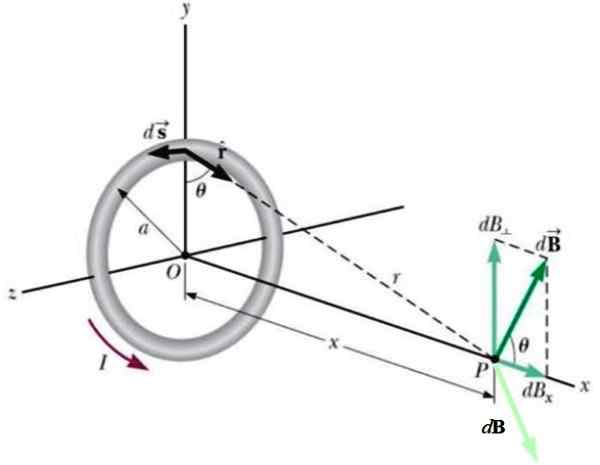Gambar 4.- Geometri untuk perhitungan bidang yang dihasilkan oleh spase melingkar pada titik p pada sumbu aksial. Sumber: Wikimedia Commons.

Elemen lain saat ini yang terletak di sisi yang berlawanan akan menghasilkan kontribusi lain untuk DB (hijau muda), sehingga komponen vertikal dibatalkan dengan yang pertama.

Hasilnya adalah bahwa medan magnet bersih bersifat horizontal, sehingga hanya terintegrasi ke dalam komponen -komponen ini, menghasilkan:

Olahraga diselesaikan

Ada kawat yang sangat panjang yang mengangkut arus 2 untuk mengalir seperti yang ditunjukkan pada gambar. Hitung besarnya medan magnet pada jarak radial 5 cm dari kawat.

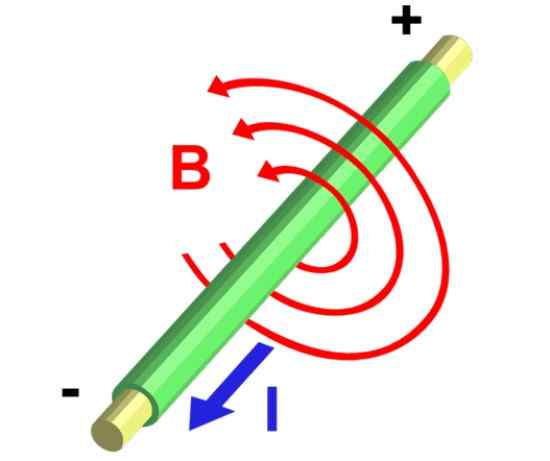Gambar 5.- Garis medan magnet dari segmen kawat bujursangkar yang mengangkut arus. Sumber: Wikimedia Commons.

Larutan

Karena ini adalah kabel yang sangat panjang, kita dapat mengambil ekspresi untuk segmen bujursangkar dan membuat θ₁= 0º dan θ₂ = 180º untuk sudut batas. Ini cukup untuk panjang kawat untuk menyimpan tak terbatas.

Dengan cara ini kita akan memiliki lapangan adalah:

Yang menyederhanakan:

Sekarang kami mengganti nilai pernyataan:

I = 2 a

R = 5 x10^-2 M

μ_{salah satu}= 4π x10^-7 T.m/ a

Arah dan rasa B Mereka ditunjukkan pada Gambar 5, di mana arah yang meninggalkan lembaran telah diambil sebagai k.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill.
2. Figueroa, d. 2005. Seri: Fisika untuk Sains dan Teknik. Volume 6. Elektromagnetisme. Diedit oleh Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fisik. Vol. 1. Edisi ke -3. di Spanyol. Perusahaan Editorial Kontinental S.KE. dari c.V.
5. Sears, Zemansky. 2016. Fisika Universitas dengan Fisika Modern. 14. Ed. Volume 1.
6. Serway, r., Jewett, J. 2008. Fisika untuk Sains dan Teknik. Volume 2. 7. Ed. Pembelajaran Cengage.