Penjelasan Hukum Kepler, Latihan, Eksperimen

Itu Hukum Kepler Tentang gerakan planet dirumuskan oleh astronom Jerman Johannes Kepler (1571-1630). Kepler menyimpulkan mereka berdasarkan karya astronom Denmarknya Tycho Brahe (1546-1601).

Brahe dengan hati -hati menyusun data dari pergerakan planet selama lebih dari 20 tahun, dengan akurasi dan akurasi yang mengejutkan, jika diperhitungkan bahwa pada saat teleskop belum ditemukan. Validitas data Anda masih valid hari ini.

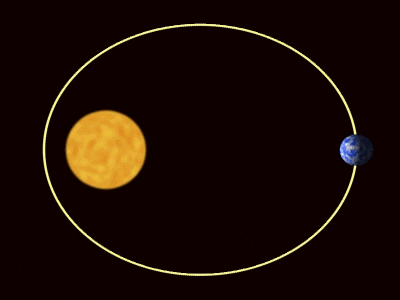Gambar 1. Orbit planet menurut hukum Kepler. Sumber: Wikimedia Commons. Willow/cc by (https: // createveCommons.Org/lisensi/oleh/3.0)

[TOC]

3 hukum Kepler

Hukum Kepler menetapkan:

-Hukum Pertama: Semua planet menggambarkan orbit elips dengan matahari di salah satu lampu sorot.

-Hukum kedua atau hukum yang sama: Garis yang diarahkan dari matahari ke planet mana pun (radio fokus), menyapu area yang sama dalam waktu yang sama.

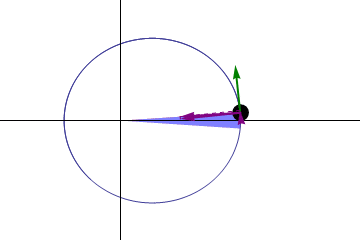Gambar 2. Hukum Area. Sumber: Wikimedia Commons. GONFER/CC BY-SA (https: // createveCommons.Org/lisensi/by-sa/3.0)

-Hukum Ketiga: Kuadrat waktu yang mengambil orbital planet mana pun di sekitar matahari sebanding dengan kubus dari jarak rata -rata ke matahari.

Menjadi T kata waktu, dipanggil Periode orbital, Dan R Jarak rata -rata, lalu:

T² sebanding dengan r³

T = k r³

Ini berarti hasil bagi T²/ R³ Itu sama untuk semua planet, yang memungkinkan untuk menghitung jari -jari orbital, jika periode orbital diketahui.

Kapan T Itu diungkapkan selama bertahun -tahun dan R Dalam unit astronomi ua*, konstanta proporsionalitas bernilai k = 1:

T²= r³

*Unit astronomi setara dengan 150 juta kilometer, yang merupakan jarak rata -rata antara bumi dan matahari. Periode orbital Bumi adalah 1 tahun.

Hukum Gravitasi Universal dan Hukum Ketiga Kepler

Hukum Gravitasi Universal menetapkan bahwa besarnya gaya tarik gravitasi antara dua objek massa M Dan M masing -masing, yang pusatnya terpisah jarak R, Itu diberikan oleh:

F = g mm /r²

G adalah konstanta gravitasi universal dan nilainya adalah G = 6.674 x 10 ^-sebelas N.M²/kg² .

Sekarang, orbit planet -planet itu berbentuk bulat panjang dengan eksentrisitas yang sangat kecil.

Ini berarti bahwa orbit tidak bergerak jauh dari lingkaran, kecuali dalam beberapa kasus seperti pluto kerdil. Jika kita memperkirakan orbit ke bentuk melingkar, percepatan gerakan planet adalah:

ke_C = v²/R

Mengingat F = ma, memiliki:

G mm /r² = m.v²/R

Di Sini v Ini adalah kecepatan linier planet di sekitar matahari, asumsi statis dan massa M, saat planet ini M. Jadi:

Dapat melayani Anda: angka penting: aturan, contoh, latihan terpecahkan

Ini menjelaskan bahwa planet -planet terjauh dari matahari memiliki kecepatan orbital yang lebih rendah, karena itu tergantung pada 1/√r.

Karena jarak yang dilalui planet ini kira -kira panjang lingkar: L = 2πr dan dibutuhkan waktu yang sama, periode orbital, diperoleh:

V = 2πr /t

Menyamakan kedua ekspresi untuk v ekspresi valid untuk t diperoleh², Kuadrat periode orbital:

Dan ini adalah hukum ketiga Kepler, karena dalam ungkapan ini tanda kurung 4π² /Gm Karena itu konstan T² sebanding dengan jarak R ditinggikan ke kubus.

Persamaan definitif untuk periode orbital diperoleh dengan mengekstraksi akar kuadrat:

Menghitung massa matahari

Berapa massa matahari? Dimungkinkan untuk mencari tahu melalui persamaan ini. Kita tahu bahwa periode orbital Bumi adalah satu tahun dan jari -jari orbital adalah 1 UA, setara dengan 150 juta kilometer, jadi kami memiliki semua data yang diperlukan.

Dalam persamaan kami sebelumnya, kami jelaskan M, tetapi tidak sebelum mengubah semua nilai ke sistem unit internasional jika:

1 tahun = 3.16 x 10⁷ detik.

1 ua = 150 juta km = 1.5 x10^sebelas M.

Dan dengan mengganti data dalam persamaan, kami memperoleh perkiraan yang cukup sukses dari matahari matahari dalam 2.0 x 10 ³⁰ kg.

Latihan

Meskipun Kepler hanya memikirkan planet -planet ketika ia memperoleh hukum terkenalnya, ini juga berlaku untuk pergerakan satelit dan badan -badan lain dari tata surya, seperti yang akan kita lihat selanjutnya.

- Latihan 1

Mengetahui bahwa orbit Jupiter adalah 5.19 kali lebih besar dari bumi, temukan periode orbital Jupiter.

Larutan

Menurut definisi unit astronomi, Jupiter berasal dari matahari 5.19 UA, oleh karena itu, menurut hukum ketiga Kepler:

T²= r³= (5.19)³ bertahun-tahun

Karena itu T = (5.19)^3/2  tahun = 11.8 tahun

- Latihan 2

Halley Comet mengunjungi matahari setiap 75.3 tahun. Menemukan:

a) Semi -mendengar orbitnya.

b) Ukuran apelium, jika perihelium berukuran 0.568 UA.

Larutan

Halley Comet mengunjungi matahari setiap 75.3 tahun. Menemukan:

a) Semi -mendengar orbitnya.

b) Ukuran apelium, jika perihelium berukuran 0.568 UA.

Solusi untuk

Ketika sebuah planet atau bintang lainnya berada pada titik yang paling dekat dengan matahari, dikatakan bahwa itu ada di perihelio, Dan saat lebih jauh, masuk aphelion. Dalam kasus khusus orbit melingkar, r dalam hukum ketiga Kepler adalah jari -jari orbit.

Dapat melayani Anda: Konstanta Antoine: Rumus, Persamaan, Contoh

Namun, dalam orbit elips tubuh selestial kurang lebih jauh dari matahari, menjadi semi -major "a" rata -rata antara aprotess dan perihelium:

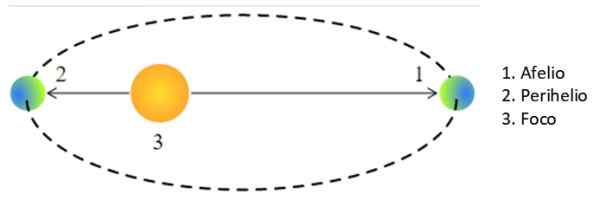
Gambar 3. Aflio dan Perihelio. Sumber: Wikimedia Commons. Pearson Scott Foresman / Domain Publik

Oleh karena itu, kami mengganti R oleh A dalam hukum ketiga Kepler, yang hasilnya untuk Halley di:

T²= a³→ a = (t)²³ → A = (75.3) ²³ Ua = 17.832 UA

Solusi b

A = ½ (perihelio + apelio)

17.832 = ½ (0.568+ aflio) → aflio = 2 x 17.832 - 0.568 ua = 35.10 ua.

Percobaan

Menganalisis pergerakan planet membutuhkan minggu, berbulan -bulan dan bahkan bertahun -tahun pengamatan dan pendaftaran yang cermat. Tetapi di laboratorium, percobaan yang sangat sederhana dapat dilakukan untuk membuktikan bahwa hukum kesetaraan Kepler terpenuhi.

Untuk ini, sistem fisik diperlukan di mana kekuatan yang mengatur gerakan adalah pusat, kondisi yang cukup untuk hukum daerah yang akan dipenuhi. Sistem seperti itu terdiri dari massa yang terikat pada tali panjang, dengan ujung utas tetap lainnya.

Adonan memisahkan sudut kecil dari posisi keseimbangannya dan dicetak sedikit impuls, sehingga mengeksekusi gerakan oval (hampir elips) pada bidang horizontal, seolah -olah itu adalah planet di sekitar matahari.

Pada kurva yang dijelaskan oleh pendulum, kita dapat membuktikan bahwa itu menyapu area yang sama di waktu yang sama, ya:

-Kami mempertimbangkan radio vektor mulai dari pusat daya tarik (titik kesetimbangan awal) hingga posisi massa.

-Dan kami barmo antara dua momen berturut -turut dengan durasi yang sama, di dua area gerakan yang berbeda.

Semakin lama benang pendulum dan semakin rendah sudut yang berangkat dari vertikal, gaya restoratif bersih akan lebih horizontal dan simulasi menyerupai kasus gerakan dengan gaya pusat dalam bidang.

Kemudian oval yang dijelaskan mendekati elips, seperti yang dilalui planet.

Bahan

-Utas yang tidak dapat dipertahankan

-1 adonan atau bola logam dicat putih yang bertindak sebagai pendulum lentil

-Penggaris

-Konveyor

-Kamera gambar dengan disk strobo otomatis

-Dukungan

-Dua Sumber Pencahayaan

-Selembar kertas atau karton hitam

Itu dapat melayani Anda: teori krisis besar: sejarah, prinsip, data untuk dan melawan

Prosedur

Perakitan gambar diperlukan untuk mengambil foto beberapa kilatan pendulum saat lintasannya mengikuti. Untuk melakukan ini, Anda harus meletakkan kamera tepat di atas pendulum dan album strobo otomatis di depan lensa.

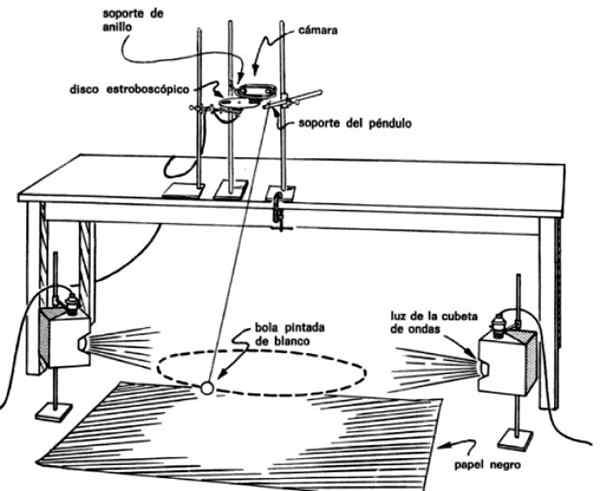Gambar 4. Majelis pendulum untuk memverifikasi bahwa itu menyapu area yang sama dalam waktu yang sama. Sumber: Panduan Laboratorium PSSC.

Dengan cara ini, gambar diperoleh pada interval waktu reguler pendulum, misalnya setiap 0.1 atau setiap 0.2 detik, yang memungkinkan untuk mengetahui waktu yang dibutuhkan untuk berpindah dari satu titik ke titik lainnya.

Anda juga harus menerangi massa pendulum dengan nyaman, meletakkan lampu di kedua sisi. Lentil harus dicat putih untuk meningkatkan kontras pada latar belakang, yang terdiri dari kertas hitam yang diperpanjang di tanah.

Sekarang Anda harus memeriksa bahwa pendulum menyapu area yang sama di waktu yang sama. Untuk ini, interval waktu dipilih dan poin yang ditempati oleh pendulum dalam interval tersebut ditandai di atas kertas.

Pada gambar, garis ditarik dari pusat oval ke titik -titik ini dan jadi kita akan memiliki yang pertama dari area yang disapu pendulum, yang kira -kira sektor elips seperti yang ditunjukkan di bawah ini:

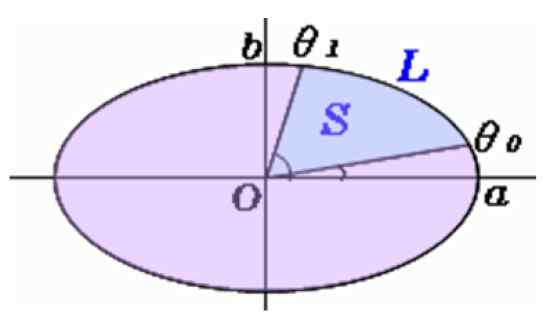Gambar 5. Area sektor elips. Sumber: f. Zapata.

Perhitungan area bagian elips

Sudut diukur dengan conveyor θ_{salah satu} Dan θ₁, Dan formula ini digunakan untuk menemukan S, luas sektor elips:

S = f (θ₁) - f (θ_{salah satu})

Dengan F (θ) diberikan oleh:

Perhatikan itu ke Dan B Mereka adalah semi -warga yang lebih besar dan kecil masing -masing. Pembaca hanya boleh dengan hati -hati mengukur semi -tert -dan sudut, karena ada kalkulator online untuk dengan mudah mengevaluasi ekspresi ini.

Namun, jika Anda bersikeras membuat perhitungan dengan tangan, Anda harus ingat bahwa sudut θ diukur dalam derajat, tetapi pada saat memasukkan data ke kalkulator, nilai -nilai harus dinyatakan dalam radianes.

Maka Anda harus menandai sepasang titik lain di mana pendulum telah menginvestasikan interval waktu yang sama, dan menggambar area yang sesuai, menghitung nilainya dengan prosedur yang sama.

Verifikasi Hukum Area yang Setara

Akhirnya masih memverifikasi bahwa hukum daerah terpenuhi, yaitu, bahwa pada waktu yang sama area yang sama adalah sapuan.

Lakukan hasilnya sedikit dari apa yang diharapkan? Anda harus ingat bahwa semua tindakan disertai dengan kesalahan eksperimental masing -masing.

Referensi

1. Kalkulator online Keisan. Area kalkulator sektor elips. Pulih dari: Keisan.Casio.com.
2. Opentax. Hukum Mosi Planet Kepler. Diperoleh dari: OpenStax.org.
3. Pssc. Fisika Laboratorium. Editorial dikembalikan. Dipulihkan dari: Buku.Google.bersama.
4. Palen, s. 2002. Astronomi. Seri Schaum. Bukit McGraw.
5. Pérez r. Sistem sederhana dengan kekuatan pusat. Pulih dari: francesphysics.Blogspot.com
6. Stern, d. Tiga hukum Kepler dari gerakan planet. Pulih dari: phy6.org.