Merek kelas

Apa itu merek kelas?

Itu Merek kelas, Juga dikenal sebagai titik tengah, itu adalah nilai yang berada di tengah kelas, yang mewakili semua nilai yang ada dalam kategori itu. Pada dasarnya, merek kelas digunakan untuk perhitungan parameter tertentu, seperti rata -rata aritmatika atau standar deviasi.

Kemudian, merek kelas adalah titik tengah dari interval apa pun. Nilai ini juga sangat berguna untuk menemukan varian set data yang sudah dikelompokkan ke dalam clas.

Distribusi frekuensi

Untuk memahami merek kelas apa diperlukan konsep distribusi frekuensi. Diberikan set data, distribusi frekuensi adalah tabel yang membagi data ini menjadi sejumlah kategori yang disebut kelas.

Tabel ini menunjukkan berapa jumlah elemen yang termasuk dalam setiap kelas; Yang terakhir dikenal sebagai frekuensi.

Dalam tabel ini, bagian dari informasi yang kami peroleh dari data dikorbankan, karena alih -alih memiliki nilai individu dari setiap elemen, kami hanya tahu bahwa itu milik kelas ini.

Di sisi lain, kami mendapatkan pemahaman yang lebih baik tentang kumpulan data, karena dengan cara ini lebih mudah untuk menghargai pola yang mapan, yang memfasilitasi manipulasi data tersebut.

Berapa banyak kelas yang dipertimbangkan?

Untuk membuat distribusi frekuensi, kami harus terlebih dahulu menentukan jumlah kelas yang ingin Anda ambil dan memilih batas kelas yang sama.

Dapat melayani Anda: tepi kubus

Pilihan berapa banyak kelas yang diperlukan harus dengan mudah, dengan mempertimbangkan bahwa sejumlah kecil kelas dapat menyembunyikan informasi tentang data yang ingin kami pelajari dan yang sangat besar dapat menghasilkan terlalu banyak detail yang tidak selalu berguna.

Faktor -faktor yang harus kita perhitungkan ketika memilih berapa banyak kelas beberapa, tetapi di antara ini adalah dua: yang pertama adalah memperhitungkan berapa banyak data yang harus kita pertimbangkan; Yang kedua adalah mengetahui berapa ukuran kisaran distribusinya (yaitu, perbedaan antara pengamatan terbesar dan terkecil).

Setelah memiliki kelas yang sudah ditentukan, kami melanjutkan untuk menghitung berapa banyak data di setiap kelas. Nomor ini disebut frekuensi kelas dan dilambangkan per fix.

Seperti yang kami katakan sebelumnya, kami memiliki distribusi frekuensi kehilangan informasi yang datang secara individual dari setiap data atau pengamatan. Oleh karena itu, suatu nilai dicari yang mewakili seluruh kelas yang berada; Nilai ini adalah classmark.

Bagaimana cara diperoleh?

Merek kelas adalah nilai sentral yang mewakili kelas. Itu diperoleh dengan menambahkan batas interval dan membagi nilai ini dengan dua. Kami dapat mengekspresikan ini secara matematis sebagai berikut:

X_yo= (Batas bawah + batas atas)/2.

Dalam ungkapan ini x_yo Menunjukkan merek kelas i-ini.

Contoh

Mengingat kumpulan data berikut, berikan distribusi frekuensi yang representatif dan dapatkan merek kelas yang sesuai.

Karena data dengan nilai numerik tertinggi adalah 391 dan anak adalah 221, kami memiliki bahwa kisarannya adalah 391 -221 = 170.

Dapat melayani Anda: probabilitas teoretis: cara mengeluarkannya, contoh, latihan

Kami akan memilih 5 kelas, semuanya dengan ukuran yang sama. Salah satu cara untuk memilih kelas adalah sebagai berikut:

Perhatikan bahwa setiap data ada di kelas, ini tidak berfungsi dan memiliki nilai yang sama. Cara lain untuk memilih kelas adalah mempertimbangkan data sebagai bagian dari variabel kontinu, yang dapat mencapai nilai riil apa pun. Dalam hal ini kita dapat mempertimbangkan kelas formulir:

205-245, 245-285, 285-325, 325-365, 365-405

Namun, cara pengelompokan data ini dapat menghadirkan ambiguitas tertentu dengan perbatasan. Misalnya, dalam kasus 245 pertanyaan muncul: kelas apa yang dimiliki, untuk yang pertama atau kedua?

Untuk menghindari kebingungan ini, konvensi poin ekstrem dibuat. Dengan cara ini, kelas pertama akan menjadi interval (205.245], yang kedua (245.285], dan sebagainya.

Setelah kelas telah ditentukan, kami melanjutkan untuk menghitung frekuensi dan kami memiliki tabel berikut:

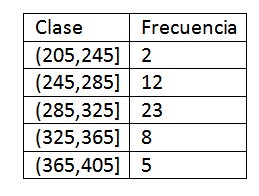
Setelah mendapatkan distribusi frekuensi data, kami melanjutkan untuk menemukan merek kelas dari setiap interval. Memang, kita harus:

X₁= (205+ 245)/2 = 225

X₂= (245+ 285)/2 = 265          

X₃= (285+ 325)/2 = 305

X₄= (325+ 365)/2 = 345

X₅= (365+ 405)/2 = 385

Kita dapat mewakili ini melalui grafik berikut:

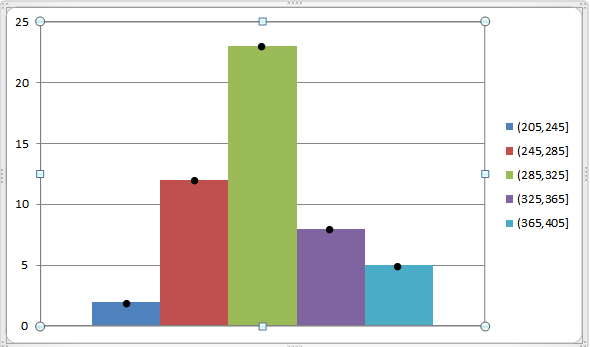
Untuk apa?

Merek kelas sangat fungsional untuk menemukan rata -rata aritmatika dan varian grup data yang telah dikelompokkan ke dalam kelas yang berbeda.

Kita dapat mendefinisikan rata -rata aritmatika sebagai jumlah pengamatan yang diperoleh antara ukuran sampel. Dari sudut pandang fisik, interpretasinya seperti titik keseimbangan dari set data.

Mengidentifikasi seluruh rangkaian data dengan satu nomor bisa berisiko, jadi Anda juga harus mempertimbangkan perbedaan antara titik keseimbangan ini dan data nyata. Nilai -nilai ini dikenal sebagai penyimpangan dari rata -rata aritmatika, dan dengan ini dicari untuk menentukan seberapa banyak rata -rata aritmatika dari data bervariasi.

Dapat melayani Anda: pecahan: jenis, contoh, latihan diselesaikan

Cara paling umum untuk menemukan nilai ini adalah karena varian, yang merupakan rata -rata kotak penyimpangan rata -rata aritmatika.

Untuk menghitung rata -rata aritmatika dan varian satu set data yang dikelompokkan dalam kelas kami menggunakan rumus berikut, masing -masing:

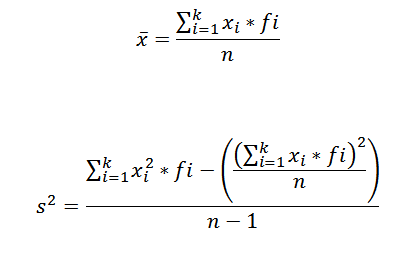
Dalam ekspresi ini x_yo  Ini adalah merek kelas i-ini, f_yo mewakili frekuensi yang sesuai dan k jumlah kelas di mana data dikelompokkan.

Contoh

Memanfaatkan data yang diberikan dalam contoh sebelumnya, kita harus memperluas sedikit lebih banyak data dalam tabel distribusi frekuensi. Berikut ini diperoleh:

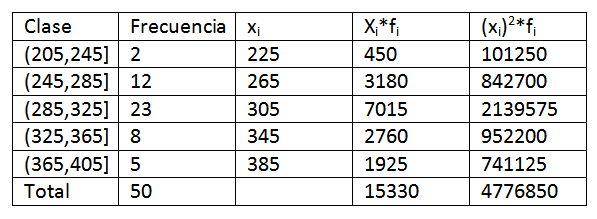
Kemudian, dengan mengganti data dalam rumus, kami telah meninggalkan bahwa rata -rata aritmatika adalah:

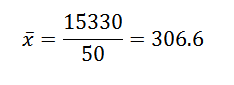
Varians dan deviasinya adalah:

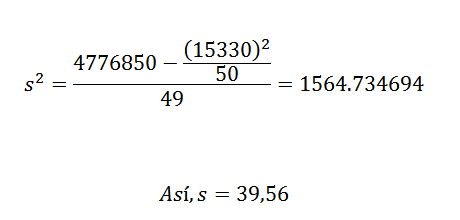
Dari sini kita dapat menyimpulkan bahwa data asli memiliki rata -rata aritmatika 306,6 dan standar deviasi 39,56.