Nomor bilangan bulat

Apa bilangan bulat?

Bilangan bulat merupakan serangkaian angka yang berguna untuk menghitung objek lengkap yang dimiliki dan yang tidak. Juga untuk menghitung yang ada di satu sisi dan yang lain dari tempat referensi tertentu.

Juga dengan seluruh angka, pengurangan atau perbedaan dapat dilakukan antara angka dan yang lain lebih besar darinya, diselesaikan sebagai hutang, misalnya. Perbedaan antara keuntungan dan hutang dibuat dengan tanda + dan - masing -masing.

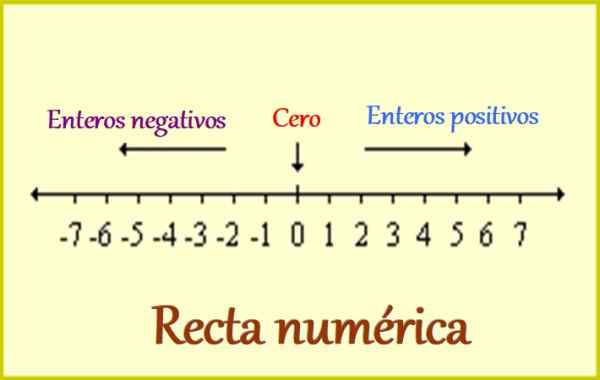
Gambar 1. Garis numerik untuk bilangan bulat. Sumber: Wikimedia Commons. Leomg/cc by-sa (https: // createveCommons.Org/lisensi/by-sa/3.0).

Itulah sebabnya seluruh seluruh angka termasuk yang berikut:

-Bilangan bulat positif, yang ditulis didahului oleh tanda +, atau hanya tanpa tanda, karena juga dipahami bahwa mereka positif. Misalnya: +1, +2, +3 ... dan seterusnya.

-0, di mana tanda itu tidak relevan, karena tidak menambahkannya untuk menguranginya dari beberapa jumlah. Tetapi 0 sangat penting, karena itu adalah referensi untuk bilangan bulat: di satu sisi yang positif berada dan negatif, seperti yang kita lihat pada sosok atas.

-Bilangan bulat negatif, yang harus selalu ditulis dari tanda -, karena dengan mereka jumlah seperti hutang dan semua yang ada di sisi lain referensi dibedakan. Contoh bilangan bulat negatif adalah: -1, -2, -3 ... dan sejak saat itu.

Bagaimana seluruh angka?

Pada awalnya kami mewakili seluruh angka dengan pengaturan set: z = ... -4, -3, -2, -1, 0, +1, +2, +3, +4 ..., yaitu, yaitu, yaitu, yaitu, yaitu, terdaftar dan terorganisir. Tetapi representasi yang sangat berguna adalah apa yang menggunakan garis numerik. Untuk ini, perlu untuk menggambar garis, yang biasanya horizontal, di mana 0 ditandai dan dibagi menjadi bagian yang identik:

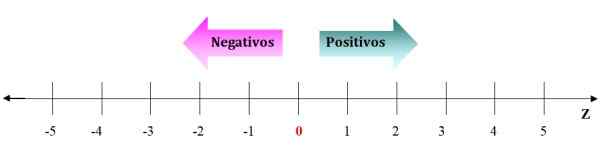Gambar 2. Representasi bilangan bulat pada garis numerik. Dari 0 ke kanan adalah bilangan bulat positif dan dari 0 ke kiri negatif. Sumber: f. Zapata.

Negatif pergi ke kiri 0 dan yang positif pergi ke kanan. Panah pada baris angka melambangkan bahwa angka terus tak terbatas. Diberikan bilangan bulat apa pun, selalu mungkin untuk menemukan satu yang lebih besar atau lebih dari yang lebih rendah.

Nilai absolut dari bilangan bulat

Nilai absolut dari bilangan bulat adalah jarak antara angka dan 0. Dan jarak selalu positif. Oleh karena itu nilai absolut dari bilangan bulat negatif adalah angka tanpa tanda lebih sedikit.

Misalnya, nilai absolut -5 adalah 5. Nilai absolut dilambangkan dengan batang, sebagai berikut:

| -5 | = 5

Untuk memvisualisasikannya, itu cukup untuk memiliki ruang pada garis numerik, dari -5 ke 0. Sedangkan nilai absolut dari bilangan bulat positif adalah angka yang sama, misalnya | +3 | = 3, karena jarak ke 0 adalah 3 spasi:

Dapat melayani Anda: Hukum Sandwich: Penjelasan dan Latihan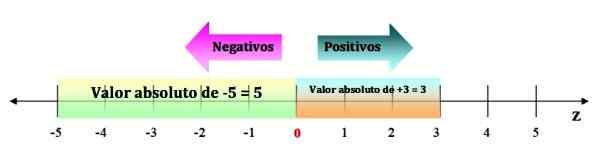Gambar 3. Nilai absolut dari bilangan bulat selalu merupakan jumlah positif. Sumber: f. Zapata.

Properti

-Himpunan bilangan bulat dilambangkan sebagai z dan mencakup set bilangan alami n, elemen mereka menjadi tak terbatas.

-Nomor bilangan bulat dan yang mengikuti (atau yang mendahului) selalu berbeda dalam unit. Misalnya, setelah 5 datang pada 6, menjadi 1 perbedaan di antara mereka.

-Setiap bilangan bulat memiliki pendahulu dan penerus.

-Bilangan bulat positif apa pun lebih besar dari 0.

-Bilangan bulat negatif selalu kurang dari 0 dan angka positif apa pun. Mari kita ambil contoh angka -100, ini kurang dari 2, dari 10 dan 50. Tetapi juga kurang dari -10, -20 dan -99 dan lebih besar dari -200.

-0 tidak memiliki pertimbangan tanda, karena tidak negatif atau positif.

-Dengan seluruh angka, operasi yang sama yang dilakukan dengan bilangan alami dapat dilakukan, yaitu: jumlah, pengurangan, perkalian, potensiasi dan banyak lagi.

-Seluruh kebalikan dari integer x tertentu, adalah -x dan jumlah bilangan bulat dengan kebalikannya adalah 0:

x + (-x) = 0.

Operasi dengan seluruh nomor

- Tambahan

-Jika angka yang akan ditambahkan memiliki tanda yang sama, nilai absolutnya ditambahkan dan hasilnya ditempatkan tanda yang dimiliki addends. Berikut beberapa contoh:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-Jika angka -angka tersebut memiliki tanda yang berbeda, nilai -nilai absolut (jurusan minor) dikurangi dan hasilnya ditempatkan tanda angka dengan nilai absolut tertinggi, sebagai berikut:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Sifat jumlah bilangan bulat

-Jumlahnya adalah komutatif, oleh karena itu urutan addends tidak mengubah jumlah. Misalkan A dan B menjadi dua bilangan bulat, dipenuhi bahwa a+b = b+a

-0 adalah elemen netral dari jumlah bilangan bulat: a + 0 = a

-Seluruh nomor yang ditambahkan dengan kebalikannya adalah 0. Kebalikan dari + a adalah -a, dan sebaliknya, kebalikan dari -a es + a. Oleh karena itu: (+ a)+ (-a) = 0.

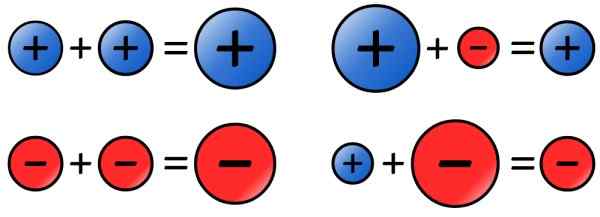Gambar 4. Aturan tanda untuk jumlah bilangan bulat. Sumber: Wikimedia Commons.

- Pengurangan

Untuk mengurangi bilangan bulat, Anda harus dipandu oleh aturan ini: Pengurangan ini setara dengan jumlah angka dengan kebalikannya. Biarkan dua angka A dan B, lalu:

A - B = A + (-B)

Misalnya, misalkan Anda perlu melakukan operasi berikut: (-3) - (+7), lalu:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Perkalian

Penggandaan bilangan bulat mengikuti aturan tertentu untuk tanda -tanda:

-Produk dari dua angka dengan Tanda yang sama Itu selalu positif.

-Saat dua angka berkembang biak tanda yang berbeda, Hasilnya selalu negatif.

Dapat melayani Anda: apa saja bagian dari fraksi? (Contoh)

-Nilai produk sama dengan mengalikan nilai absolut masing -masing.

Segera beberapa contoh yang mengklarifikasi hal di atas:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Sifat penggandaan bilangan bulat

-Multiplikasi adalah komutatif. Menjadi dua bilangan bulat a dan b, memang benar bahwa: a.b = b.A, yang juga dapat dinyatakan sebagai:

Urutan faktor tidak mengubah produk.

-Elemen netral dari perkalian adalah 1. Menjadi bilangan bulat, karena itu.1 = 1

-Setiap bilangan bulat dikalikan 0 sama dengan 0: a.0 = 0

Properti distributif

Perkalian memenuhi properti distributif sehubungan dengan jumlah tersebut. Ya A, B dan C adalah seluruh angka lalu:

ke.(b +c) = a.b + a.C

Kemudian contoh cara menerapkan properti ini:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 -33 = 12 + (-33) = -21

Potensiasi

-Jika basisnya positif, hasil operasi selalu positif.

-Ketika basis negatif, jika eksponen genap, hasilnya positif. Dan jika eksponen aneh, hasilnya negatif.

- Divisi

Di Divisi aturan tanda yang sama berlaku seperti dalam perkalian:

-Dengan membagi dua bilangan bulat dari tanda yang sama, hasilnya selalu positif.

-Ketika dua bilangan bulat dari berbagai tanda dibagi, hasil bagi negatif.

Misalnya:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Penting: Divisi ini tidak komutatif, dengan kata lain untuk ÷ b ≠ b ÷ a dan seperti biasa, pembagian antara 0 tidak diperbolehkan.

- Potensiasi

Jadilah bilangan bulat dan kami ingin menaikkannya ke eksponen n, maka kita harus berlipat ganda dengan sendirinya, seperti yang ditunjukkan di bawah ini:

ke^N = a.ke.ke.ke.… ke

Mari kita juga mempertimbangkan yang berikut, dengan mempertimbangkan bahwa N adalah angka alami:

-Jika a negatif dan n genap, hasilnya positif.

-Ketika a negatif dan n itu aneh, itu menghasilkan angka negatif.

-Jika a positif dan n genap atau aneh, itu selalu merupakan bilangan bulat positif.

-Setiap bilangan bulat yang diangkat ke 0 sama dengan 1: a⁰ = 1

-Setiap angka tinggi ke 1 sama dengan angka: a¹ = a

Mari kita berikan misalnya yang ingin Anda temukan (-3)⁴ , Untuk membuatnya berkembang biak (-3) empat kali dengan sendirinya, seperti ini: (-3).(-3).(-3).(-3) = 81.

Contoh lain, juga dengan bilangan bulat negatif adalah:

(-2)³ = (-2).(-2).(-2) = -8

Produk kekuatan dasar yang sama

Misalkan dua kekuatan dengan dasar yang sama, jika kita melipatgandakannya, kita mendapatkan kekuatan lain dengan basis yang sama, yang eksponennya adalah jumlah dari eksponen yang diberikan:

ke^N ·ke^M = a^{n + m}

Rasio bedak dasar yang sama

Dengan membagi kekuatan dari basis yang sama, hasilnya adalah kekuatan dengan basis yang sama, yang eksponennya adalah pengurangan dari eksponen yang diberikan:

Dapat melayani Anda: sudut di lingkar: jenis, sifat, latihan terpecahkan

ke^N ÷ a^M = a^{n - m}

Kemudian dua contoh yang mengklarifikasi poin -poin ini:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Contoh

Mari kita lihat contoh -contoh sederhana untuk menerapkan aturan -aturan ini, mengingat bahwa dalam kasus bilangan bulat positif, tanda itu dapat dikeluarkan dengan:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

D) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

h) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Latihan terpecahkan

- Latihan 1

Semut bergerak pada garis angka Gambar 1. Mulai dari titik x = +3 melakukan perpindahan berikut:

-7 unit bergerak ke kanan

-Sekarang 5 unit dikembalikan ke kiri

-Berjalan 3 unit ke kiri.

-Itu kembali dan bergerak 4 unit ke kanan.

Pada titik mana semut di akhir rute?

Larutan

Sebutkan perpindahannya. Ketika mereka berada di sebelah kanan, mereka diberi tanda positif dan ketika mereka berada di tanda negatif kiri. Dengan cara ini, dan mulai dari x = +3 yang Anda miliki:

-D pertama: x₁ = +3 +7 = +10

-D kedua: x₂ = +10 +(-5) = +5

-D ketiga D: x₃ = +5 +(-3) = +2

-Keempat D: x₄ = +2 +4 = +6

Saat semut mengakhiri jalannya berada di posisi x = +6. Artinya, 6 unit di sebelah kanan 0 pada garis numerik.

- Latihan 2

Selesaikan operasi berikut:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Larutan

Operasi ini berisi tanda -tanda pengelompokan, yang merupakan tanda kurung, kurung persegi dan kunci. Saat memecahkan, Anda harus mengurus tanda kurung terlebih dahulu, setelah kurung persegi dan akhirnya kunci. Dengan kata lain, Anda harus bekerja dari dalam ke luar.

Dalam latihan ini, intinya mewakili perkalian, tetapi dalam hal antara satu angka dan tanda kurung atau simbol lainnya tidak ada gunanya, dengan cara yang sama dipahami bahwa itu adalah produk.

Selanjutnya, resolusi langkah demi langkah, warna berfungsi sebagai panduan untuk mengikuti hasil pengurangan tanda kurung, yang merupakan simbol kelompok paling internal:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] =

= 36 + [16].-[-1] -4] =

= 52.1- 4] = 52.-3 = -156

- Latihan 3

Selesaikan persamaan tingkat pertama:

12 + x = 30 + 3x

Larutan

Istilah dikelompokkan dengan yang tidak diketahui di sebelah kiri kesetaraan, dan istilah numerik di sebelah kanan:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9