Kotak terkecil

Apa metode kuadrat minimum?

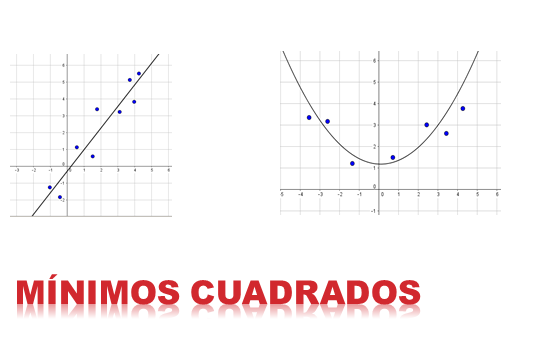
Metode Kotak terkecil Ini adalah salah satu aplikasi terpenting dalam pendekatan fungsi. Idenya adalah untuk menemukan kurva sedemikian rupa sehingga, mengingat satu set pasangan yang rapi, fungsi ini lebih dekat didekati untuk data. Fungsi bisa berupa garis, kurva kuadratik, kubik, dll.

Gagasan metode ini adalah untuk meminimalkan jumlah kotak perbedaan dalam ordinat (komponen y), antara titik -titik yang dihasilkan oleh fungsi yang dipilih dan titik -titik yang termasuk dalam set data.

Metode kuadrat minimum

Sebelum memberikan metode ini, pertama -tama kita harus jelas tentang apa "lebih baik mendekat". Misalkan garis dicari y = b+mx yang paling mewakili satu set poin, yaitu (x1, y1), (x2, y2) ..., (xn, yn).

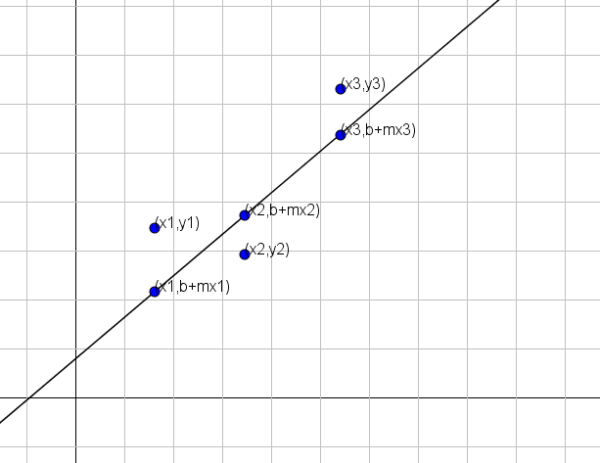
Seperti yang ditunjukkan pada gambar sebelumnya, jika variabel x dan y terkait dengan garis y = b+mx, maka untuk x = x1 nilai y yang sesuai akan menjadi b+mx1. Namun, nilai ini berbeda dari nilai sebenarnya dari y, yaitu y = y1.

Ingatlah bahwa di pesawat, jarak antara dua titik diberikan oleh formula berikut:

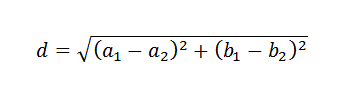
Dengan mengingat hal ini, untuk menentukan cara memilih garis y = b+mx yang paling baik mendekati data yang diberikan, kedengarannya logis untuk digunakan sebagai kriteria pemilihan garis yang meminimalkan jumlah kotak jarak antara titik -titik tersebut dan garis.

Karena jarak antara titik (x1, y1) dan (x1, b+mx1) adalah y1- (b+mx1), masalah kita dikurangi untuk menemukan angka m dan b sehingga jumlah berikutnya minimal:

Dapat melayani Anda: Teorema Hijau, Demonstrasi, Aplikasi dan Latihan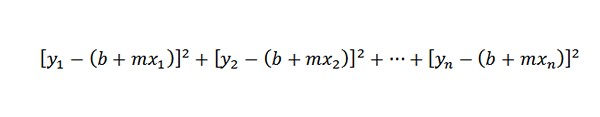

Garis yang memenuhi kondisi ini dikenal sebagai "pendekatan ke garis kotak minimum ke titik (x1, y1), (x2, y2), ..., (xn, yn)".

Setelah masalah diperoleh, masih ada untuk memilih metode untuk menemukan pendekatan dengan kotak minimum. Jika titik (x1, y1), (x2, y2), ..., (xn, yn) semuanya ada di garis y = mx+b, kita harus menjadi colineal dan:

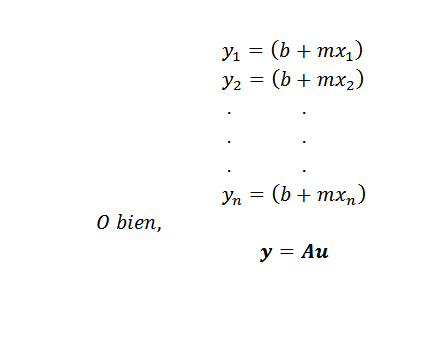
Dalam ungkapan ini:

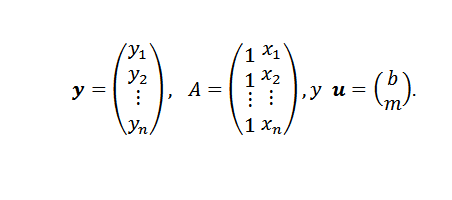
Akhirnya, jika poinnya tidak kolineal, maka y-au = 0 dan masalahnya dapat diterjemahkan menjadi menemukan vektor atau sedemikian rupa sehingga standar Euclidean minimal.

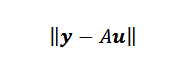
Menemukan vektor yang meminimalkan atau tidak sesulit yang Anda pikirkan. Karena A adalah matriks NX2 dan U adalah matriks 2 × 1, kami memiliki vektor Au adalah vektor dalam R^N dan termasuk dalam gambar A, yang merupakan subruang dari R^N Dengan dimensi tidak lebih dari dua.

Kami akan berasumsi bahwa n = 3 untuk menunjukkan apa prosedur yang harus diikuti. Jika n = 3, gambar A akan menjadi pesawat atau garis yang melewati asal.

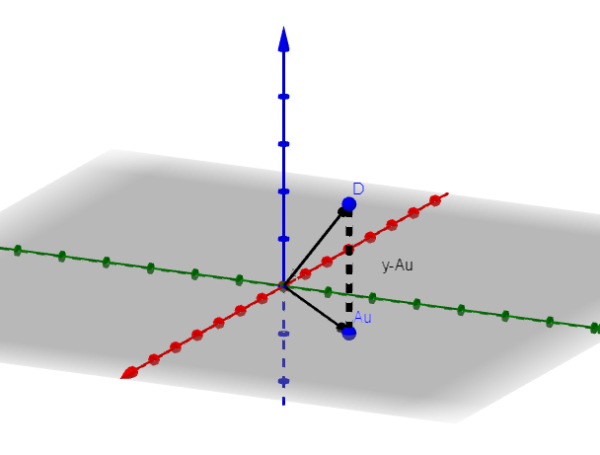
Biarkan v vektor yang meminimalkan. Pada gambar kami mengamati bahwa y-au diminimalkan ketika itu ortogonal dengan gambar a. Yaitu, jika V adalah vektor yang meminimalkan, maka itu terjadi itu:

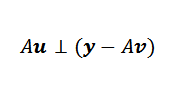
Kemudian, kita dapat mengekspresikan hal di atas dengan cara ini:

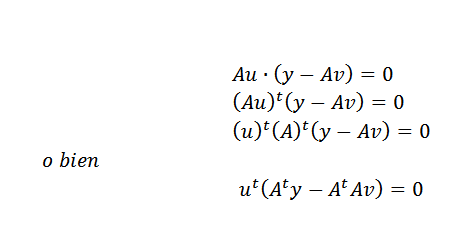
Ini hanya bisa terjadi jika:

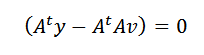
Akhirnya, membersihkan V, kita harus:

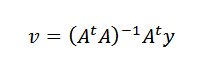
Dimungkinkan untuk melakukan ini karena^TA dibalik setiap kali titik N sebagai data bukan colineal.

Sekarang, jika alih -alih mencari garis, kami ingin menemukan perumpamaan (yang ekspresinya akan dari bentuk y = a+bx+cx²) Bahwa itu adalah perkiraan yang lebih baik untuk titik data, prosedur akan dijelaskan di bawah ini.

Dapat melayani Anda: bilangan bulat

Jika titik data berada di perumpamaan itu, itu harus:

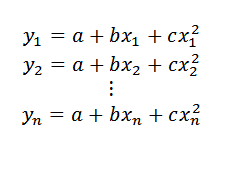
Kemudian:

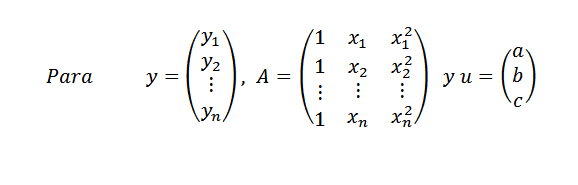
Demikian pula kita bisa menulis y = au. Jika semua poin tidak ada dalam perumpamaan, kami memiliki bahwa y-au berbeda dari nol untuk vektor u dan masalah kami lagi: temukan vektor u dalam r3 sedemikian rupa sehingga norma || y-au || sebanyak mungkin.

Mengulangi prosedur sebelumnya, kita bisa mencapai vektor yang diinginkan adalah:

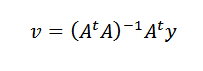
Latihan terpecahkan

Latihan 1

Temukan garis yang paling sesuai dengan poin (1.4), (-2.5), (3, -1) dan (4.1).

Larutan

Kita harus:

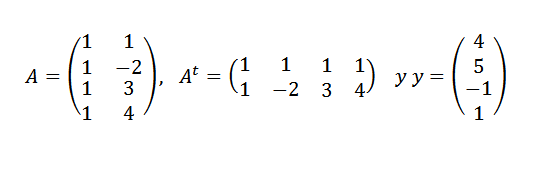
Kemudian:

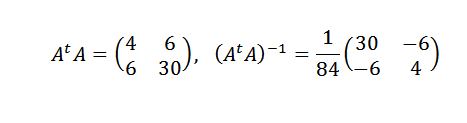
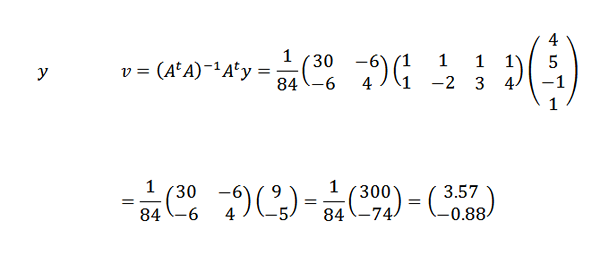
Karena itu, kami menyimpulkan bahwa garis yang paling sesuai dengan poin yang diberikan oleh:

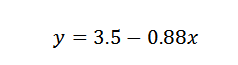
Latihan 2

Misalkan sebuah objek dijatuhkan dari ketinggian 200 m. Saat jatuh, langkah -langkah berikut diambil:

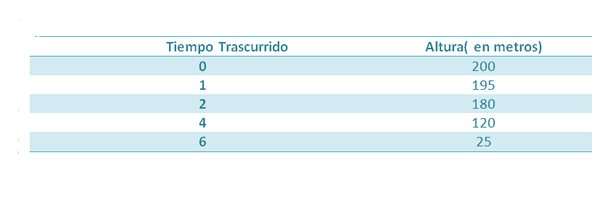
Kita tahu bahwa ketinggian objek ini, setelah beberapa waktu berlalu, diberikan oleh:

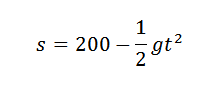
Jika kita ingin mendapatkan nilai G, kita dapat mencari perumpamaan yang merupakan pendekatan yang lebih baik untuk lima titik yang diberikan dalam tabel, dan dengan demikian kita akan memiliki koefisien yang menyertai t² Ini akan menjadi pendekatan yang masuk akal untuk (-1/2) g jika pengukurannya tepat.

Kita harus:

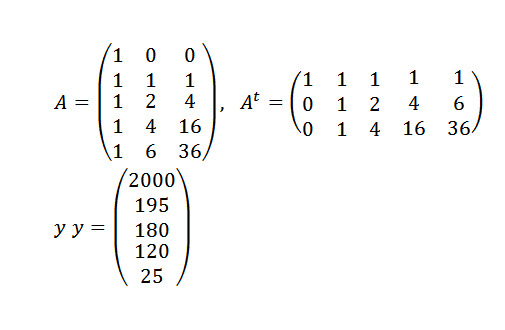
Kemudian:

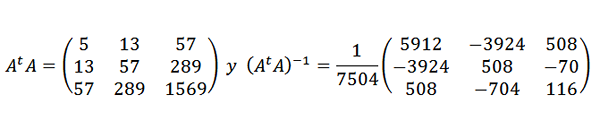
Jadi titik data disesuaikan dengan ekspresi kuadratik berikut:

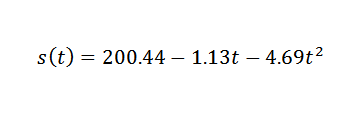
Jadi Anda harus:

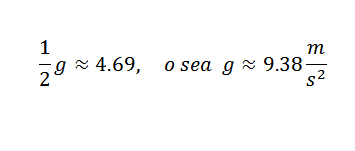
Ini adalah nilai yang cukup dekat dengan yang benar, yaitu g = 9,81 m/s². Untuk mendapatkan G yang lebih akurat dari G, perlu untuk memulai dari pengamatan yang lebih tepat.

Untuk apa metode minimum kuadrat?

Dalam masalah yang terjadi dalam ilmu alam atau sosial, lebih mudah untuk menulis hubungan antara variabel yang berbeda melalui beberapa ekspresi matematika.

Dapat melayani Anda: variasi proporsional

Misalnya, kita dapat menceritakan dalam ekonomi biaya (c), pendapatan (i) dan laba (u) melalui formula sederhana:

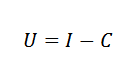
Dalam fisika, kita dapat menghubungkan akselerasi yang disebabkan oleh gravitasi, waktu di mana suatu objek telah jatuh dan ketinggian objek oleh hukum:

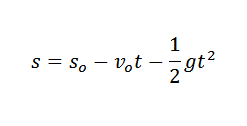
Dalam ungkapan sebelumnya S_{salah satu} Ini adalah ketinggian awal objek tersebut dan v_{salah satu} adalah kecepatan awal Anda.

Namun, menemukan formula seperti ini bukanlah tugas yang sederhana; Biasanya sesuai dengan profesional yang bertugas untuk bekerja dengan banyak data dan berulang kali melakukan beberapa percobaan (untuk memverifikasi bahwa hasil yang diperoleh konstan) untuk menemukan hubungan antara data yang berbeda.

Cara umum untuk mencapai hal ini adalah dengan mewakili data yang diperoleh dalam bidang sebagai titik dan mencari fungsi kontinu yang secara optimal mendekati titik -titik ini.

Salah satu cara untuk menemukan fungsi yang "mendekati lebih baik" data yang diberikan adalah dengan metode minimum kuadrat.

Selain itu, seperti yang juga kita lihat dalam latihan, berkat metode ini kita dapat mencapai pendekatan yang cukup dekat dengan konstanta fisik.