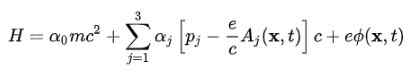Model Aomic Karakteristik Dirac Jordan dan Deposulat

Dia Model Atom Dirac-Jordan Itu adalah generalisasi relativistik dari operator Hamiltonian dalam persamaan yang menggambarkan fungsi gelombang kuantum. Berbeda dengan model sebelumnya, Schrodinger, tidak perlu memaksakan putaran melalui prinsip pengecualian Pauli, karena tampaknya secara alami.

Selain itu, model Dirac-Jordan menggabungkan koreksi relativistik, interaksi spin-organ dan istilah Darwin, yang memperhitungkan struktur halus tingkat elektronik atom.

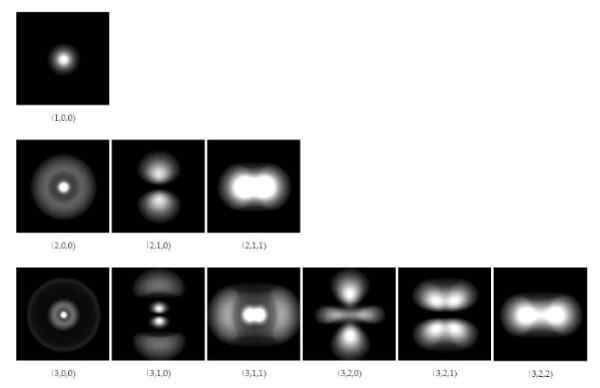
Gambar 1. Orbital elektronik dalam atom hidrogen untuk tiga tingkat energi pertama. Sumber: Wikimedia Commons.

Pada 1928, para ilmuwan Paul A. M. Dirac (1902-1984) dan Pascual Jordan (1902-1980), diusulkan untuk menggeneralisasi mekanika kuantum yang dikembangkan oleh Schrodinger, untuk memasukkan koreksi relativitas khusus Einstein.

Dirac bagian dari persamaan Schrodinger, yang terdiri dari operator diferensial, yang disebut Hamiltonian, yang beroperasi pada fungsi yang dikenal sebagai Fungsi gelombang elektron. Namun, Schrodinger tidak memperhitungkan efek relativistik.

Solusi fungsi gelombang memungkinkan untuk menghitung daerah di mana elektron di sekitar nukleus akan ditemukan dengan tingkat probabilitas tertentu. Daerah atau area ini disebut Orbital Dan mereka bergantung pada angka kuantum diskrit tertentu, yang menentukan energi dan momentum sudut elektron. 

[TOC]

Dalil

Dalam teori mekanik kuantum, apakah relativistik atau tidak, tidak ada konsep orbit, karena posisi maupun kecepatan elektron tidak dapat ditentukan secara bersamaan. Dan di samping itu, menentukan salah satu variabel menyebabkan ketidaktepatan total di yang lain.

Untuk bagiannya, Hamiltonian adalah operator matematika yang bertindak pada fungsi gelombang kuantum dan dibangun dari energi elektron. Misalnya, elektron bebas memiliki energi total dan itu tergantung pada momentum liniernya P dengan demikian:

E = (P²)/ 2m

Untuk membangun Hamiltonian, itu dimulai dari ungkapan ini dan diganti P Oleh operator kuantum untuk momentum: 

P = -I ħ ∂ /∂R 

Penting untuk dicatat bahwa persyaratan P Dan P Mereka berbeda, karena yang pertama adalah momentum dan yang lainnya adalah Operator diferensial terkait dengan momentum. 

Dapat melayani Anda: model atom leukipo: postulat, keterbatasan, kepentingan

Selain itu, saya adalah unit imajiner dan ħ Konstanta Planck dibagi dengan 2π, dengan cara ini operator Hamiltonan dari elektron bebas diperoleh:

H = (ħ²/2m) ∂² /∂R² 

Untuk menemukan Hamiltonian dari elektron dalam atom, interaksi elektron dengan nukleus ditambahkan: 

H = (ħ2/2m) ∂² /∂R²  - Eφ (r)

Dalam ekspresi sebelumnya -e adalah muatan listrik elektron dan φ (r) potensial elektrostatik yang diproduksi oleh nukleus pusat.

Sekarang, operator H bertindak pada fungsi gelombang ψ sesuai dengan persamaan Schrodinger, yang ditulis seperti ini:

H ψ = (i ħ ∂ /∂t) ψ

Empat dalil Dirac

Postulat pertama: Persamaan gelombang relativistik memiliki struktur yang sama dengan persamaan gelombang Schrodinger, apa perubahannya h:

H ψ = (i ħ ∂ /∂t) ψ

Postulat kedua: Operator Hamiltonian dibangun berdasarkan hubungan energi-momentum Einstein, yang ditulis seperti ini:

E = (m² C⁴ + P² C²)^1/2

Dalam hubungan sebelumnya, jika partikel memiliki momentum p = 0 maka Anda memiliki persamaan terkenal E = mc² yang menghubungkan energi istirahat dari massa massa M dengan kecepatan cahaya c.

Postulat ketiga: Untuk mendapatkan operator Hamiltonian, aturan kuantisasi yang sama yang digunakan dalam persamaan Schrodinger digunakan:

P = -I ħ ∂ /∂R

Pada awalnya, tidak jelas bagaimana menangani operator diferensial yang bertindak dalam akar kuadrat ini, jadi Dirac berangkat untuk mendapatkan operator Hamiltonian linier dalam operator momentum dan dari sana muncul postulat keempatnya.

Ruang postulat: Untuk menyingkirkan akar kuadrat dalam rumus energi relativistik, Dirac mengusulkan struktur berikut untuk e²:

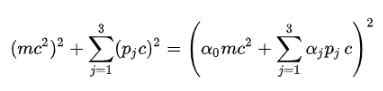
Tentu saja, perlu untuk menentukan koefisien alfa (α0, α1, α2, α3) sehingga ini terpenuhi.

Persamaan Dirac

Persamaan Dirac pertama kali dinaikkan untuk elektron bebas, menggunakan struktur yang diusulkan dalam postulat keempat. Tetap sebagai berikut: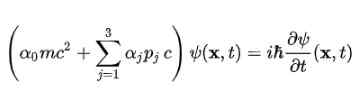

Itu dapat melayani Anda: Dengar Kekuatan: Kekuatan Permukaan dan Massa

Dalam bentuknya yang ringkas, persamaan Dirac dianggap sebagai salah satu persamaan matematika terindah di dunia:

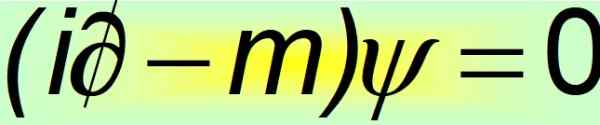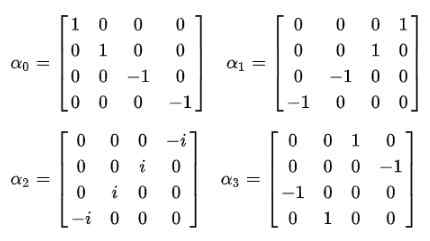
Gambar 2. Persamaan Dirac Compact. Sumber: f. Zapata.

Dan saat itulah dibuktikan bahwa alfas konstan tidak bisa menjadi jumlah skalar. Satu -satunya cara di mana kesetaraan postulat keempat terpenuhi adalah bahwa mereka adalah 4 × 4 matriks konstan, yang dikenal sebagai Matriks Dirac:

Segera diamati bahwa fungsi gelombang berhenti menjadi fungsi skalar dan menjadi vektor empat -komponen Espinor:

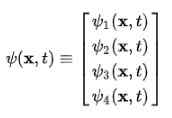
Atom Dirac-Jordan

Untuk mendapatkan model atom, perlu dipindahkan dari persamaan elektron bebas ke elektron dalam medan elektromagnetik yang diproduksi oleh nukleus atom. Interaksi ini diperhitungkan dengan memasukkan skalar potensial φ dan vektor potensial KE Di Hamiltonian:

Fungsi Gelombang (Espinor) yang dihasilkan dari menggabungkan Hamiltonian ini memiliki karakteristik berikut: 

- Itu memenuhi relativitas khusus, karena memperhitungkan energi intrinsik elektron (istilah pertama dari Hamiltonian relativistik)

- Ini memiliki empat solusi yang sesuai dengan empat komponen Espinor

- Dua solusi pertama sesuai dengan satu untuk memutar +½ dan yang lainnya ke putaran - ½ 

- Akhirnya, dua solusi lainnya memprediksi keberadaan antimateri, karena mereka sesuai dengan positron lawan yang berlawanan.

Keuntungan besar dari persamaan Dirac adalah bahwa koreksi dasar Hamiltonian dari Schrodinger H (O) dapat dipecah menjadi beberapa istilah yang akan kami tunjukkan di bawah ini:

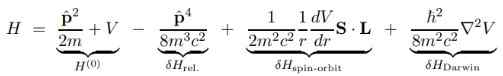
Dalam ekspresi sebelumnya v adalah skalar potensial, karena vektor potensial KE Itu batal jika seharusnya proton stasioner pusat dan itulah sebabnya tidak muncul.

Alasan mengapa koreksi Dirac mengenai solusi Schrodinger dalam fungsi gelombang halus. Mereka muncul dari fakta bahwa tiga istilah terakhir dari Hamiltonian yang dikoreksi semuanya dibagi dengan kecepatan C dari alun -alun, angka yang sangat besar, yang membuat istilah -istilah ini secara numerik kecil.

Ini dapat melayani Anda: Vy Canis Majoris: Penemuan, Karakteristik, Struktur, Pelatihan dan Evolusi

Koreksi relativistik dengan spektrum energi

Menggunakan persamaan DIC-Jordan, koreksi ditemukan pada spektrum energi elektron dalam atom hidrogen. Ada juga koreksi energi dalam atom dengan lebih dari satu elektron kira -kira melalui metodologi yang dikenal sebagai teori gangguan.

Demikian pula, model Dirac memungkinkan Anda untuk menemukan koreksi struktur halus pada tingkat energi hidrogen. 

Namun, bahkan koreksi yang lebih halus seperti struktur hyperfine dan pergeseran domba diperoleh dari model yang lebih maju seperti Teori Kuantum Campos, lahir justru karena kontribusi model Dirac.

Gambar berikut menunjukkan bagaimana koreksi relativistik Dirac berada pada tingkat energi:

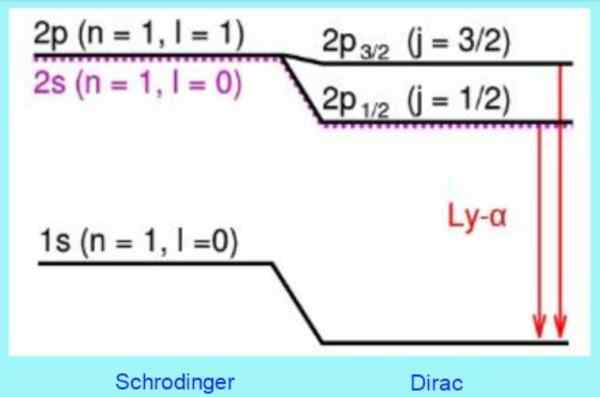Gambar 3. Koreksi model Dirac pada tingkat atom hidrogen. Sumber: Wikimedia Commons.

Misalnya, solusi untuk persamaan DIRAC dengan benar memprediksi pergeseran yang diamati pada level 2s. Ini adalah koreksi struktur halus yang diketahui dengan baik di garis Lyman - Alfa dari spektrum hidrogen (lihat Gambar 3).

Ngomong -ngomong, struktur halus adalah nama yang menerima dalam fisika atom yang membuka garis spektrum emisi atom, yang merupakan konsekuensi langsung dari putaran elektronik.

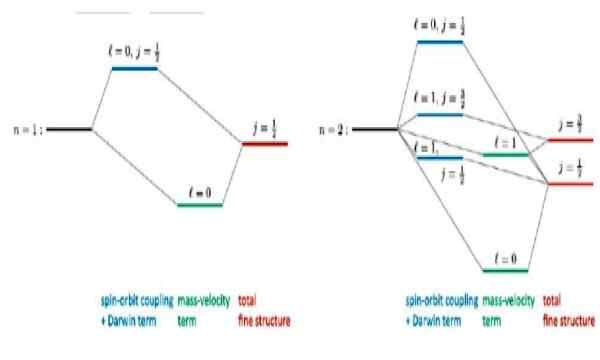Gambar 4. Struktur halus berlangsung untuk keadaan dasar n = 1 dan keadaan tereksitasi pertama n = 2 dalam atom hidrogen. Sumber: r Wirnata. Koreksi relativistik dengan atom seperti hidrogen. ResearchGate.bersih

Artikel yang menarik

Model Atom Broglie.

Model Atom Chadwick.

Model Atom Heisenberg.

Model Atom Perrin.

Model Atom Thomson.

Model Atom Dalton.

Model Atom Schrödinger.

Model Atom Demokritus.

Model Atom Leucipo.

Model Atom Bohr.

Model atom saat ini.

Referensi

1. Teori atom. Pulih dari Wikipedia.org.
2. Momen magnetik elektron. Pulih dari Wikipedia.org.
3. Quanta: Buku Pegangan Konsep. (1974). Oxford University Press. Pulih dari Wikipedia.org.
4. Dirac Jordan Atomic Model. Pulih dari prezi.com.
5. Alam semesta kuantum baru. Cambridge University Press. Pulih dari Wikipedia.org.