Gerakan relatif dalam dimensi, dalam dua dimensi, latihan

Dia Gerakan Relatif dari suatu partikel atau objek adalah yang diamati sehubungan dengan titik referensi tertentu yang telah dipilih oleh pengamat, yang mungkin diperbaiki atau bergerak. Kecepatan selalu mengacu pada beberapa sistem koordinat yang digunakan untuk menggambarkannya.

Misalnya, co -pilot mobil yang bergerak dan itu perjalanan dengan nyaman tertidur di kursinya adalah istirahat sehubungan dengan pengemudi, tetapi ia bukan untuk pengamat yang berdiri di trotoar yang melihat mobil pass.

Gambar 1. Pesawat terbang mempertahankan kecepatan relatif tertentu di antara mereka saat berlatih akrobat. Sumber: Pixabay.

Maka gerakan itu selalu relatif, tetapi kebetulan bahwa sistem koordinat atau referensi biasanya dipilih, memiliki asal -usulnya di bumi atau tanah, tempat yang dianggap sebagai stasioner. Dengan cara ini kekhawatiran ini berfokus pada menggambarkan pergerakan objek yang diteliti.

Apakah mungkin untuk menggambarkan kecepatan co -co -criver sehubungan dengan penumpang yang bepergian dengan mobil lain? Jawabannya iya. Ada kebebasan untuk memilih nilai (x_{salah satu}, Dan_{salah satu}, z_{salah satu}): Asal usul sistem referensi. Seleksi ini sewenang -wenang dan tergantung pada preferensi pengamat, serta kemudahan yang Anda berikan untuk resolusi masalah.

[TOC]

Gerakan relatif dalam dimensi

Ketika gerakan melewati garis lurus, ponsel memiliki kecepatan dalam arah yang sama atau di arah yang berlawanan, keduanya dilihat oleh pengamat yang berdiri di darat (t). Apakah pengamat bergerak mengenai ponsel? Ya, dengan kecepatan yang sama mereka bawa, tetapi di arah yang berlawanan.

Bagaimana bergerak seluler sehubungan dengan yang lain? Untuk mengetahui kecepatan ditambahkan vektor.

Itu dapat melayani Anda: Pluto (planet kerdil)

-Contoh 1

Mengacu pada gambar yang ditunjukkan, tunjukkan kecepatan relatif mobil 1 sehubungan dengan mobil 2 di setiap situasi.

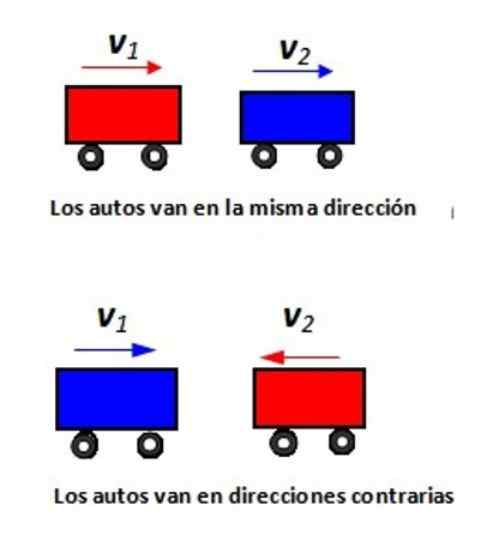Gambar 2. Dua mobil pergi di jalan bujursangkar: a) ke arah yang sama dan b) dalam arah yang berlawanan.

Larutan

Kami akan menetapkan tanda positif ke kecepatan ke kanan, dan tanda negatif di sebelah kiri. Jika ponsel menuju ke kanan pada 80 km/jam, penumpang di ponsel ini melihat pengamat di tanah bergerak ke - 80 km/jam.

Misalkan semuanya terjadi di sepanjang sumbu x. Pada gambar berikut, mobil merah bergerak pada +100 km/jam (terlihat dari T) dan bersiap untuk melewati mobil biru yang bergerak pada +80 km/jam (juga terlihat dari T). Dengan kecepatan apa Anda melihat seorang penumpang mendekati mobil merah di mobil biru?

Labelnya adalah: v _1/2 Kecepatan otomatis 1 sehubungan dengan 2, v_1/t Kecepatan mobil sehubungan dengan T, v_T/2 Kecepatan tabel sehubungan dengan 2. Menambahkan vektorial:

v_1/2 = v_1/t + v_T/2 = (+100 km/jam - 80 km/jam) X= 20 km/jam X

Kita bisa melakukannya tanpa notasi vektor. Perhatikan subskrip: Mengalikan keduanya di sebelah kanan harus mendapatkan yang di sebelah kiri.

Dan saat mereka berada di arah yang berlawanan? Sekarang v_1/t = + 80 km/jam dan v_2/t = -100 km/jam, oleh karena itu v_T/2 = + 100 km/jam. Penumpang Auto Blue akan melihat mobil merah mendekat:

v_{1/2 =} v_1/t + v_T/2 = +80 km/jam +100 km/jam = 180 km/jam

Gerakan relatif dalam dua dan tiga dimensi

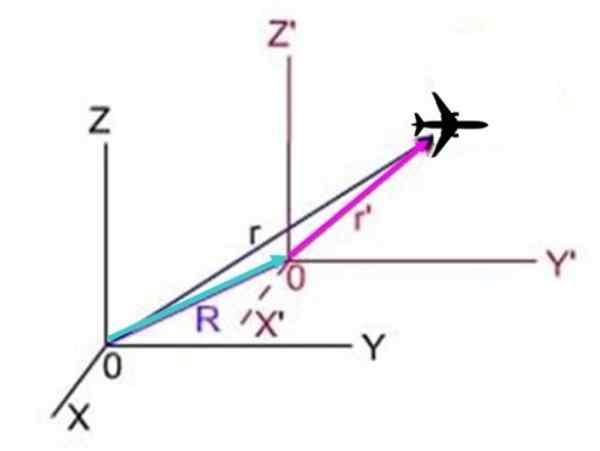
Dalam skema berikut, R Itu adalah posisi pesawat yang terlihat dari sistem X dan z, R'Ini adalah posisi dari sistem X dan z ' Dan R Itu adalah posisi sistem dengan premium sehubungan dengan sistem tanpa premium. Tiga vektor membentuk segitiga di mana R + R'= R, Karena itu R'= r - r.

Gambar 3.- Pesawat bergerak sehubungan dengan dua sistem koordinat, pada gilirannya salah satu sistem bergerak sehubungan dengan yang lain.

Karena turunan sehubungan dengan waktu posisi adalah kecepatan, hasilnya:

Dapat melayani Anda: Tembakan Parabola: Karakteristik, Rumus dan Persamaan, Contoh

v'= v - atau

Dalam persamaan ini v'Ini adalah kecepatan pesawat sehubungan dengan sistem X dan z ', v adalah kecepatan sehubungan dengan sistem X dan z Dan atau Ini adalah kecepatan konstan dari sistem utama sehubungan dengan sistem tanpa premi.

-Latihan diselesaikan 2 

Pesawat berada di arah utara dengan kecepatan sehubungan dengan udara 240 km/jam. Tiba -tiba mulai meniup angin dari barat ke timur dengan kecepatan 120 km/ menurut bumi.

Temukan: a) kecepatan pesawat sehubungan dengan bumi, b) penyimpangan yang dialami oleh pilot c) koreksi yang harus dilakukan pilot untuk dapat menunjuk langsung ke utara dan kecepatan baru sehubungan dengan tanah, sekali Koreksi telah dibuat.

Larutan

a) Elemen -elemen berikut dimiliki: Pesawat (A), Bumi (T) dan Angin (V).

Dalam sistem koordinat di mana utara adalah + dan dan arah barat adalah + x Ada kecepatan yang diberikan dan label masing-masing (subskrip):

v _Av = 240 km/jam (+Dan); v _V/t = 120 km/jam (+X); v _Pada = ?

Jumlah vektor yang memadai adalah:

v _Pada = v _Av + v _V/t = 240 km/jam (+Dan) + 120 km/jam (+X)

Besarnya vektor ini adalah: v _Pada = (240 ²+ 120²)^1/2 km/h = 268.3 km/jam

b) θ = arctg (v _Av / v _V/t) = arctg (240/120) = 63.Ke -4 utara timur atau 26.Timur Laut ke -6.

c) Untuk melanjutkan ke utara dengan angin ini, Anda harus mengarahkan busur pesawat ke barat laut, sehingga angin mendorongnya langsung ke utara. Dalam hal ini, kecepatan pesawat yang terlihat dari tanah akan berada di +dan, sedangkan kecepatan pesawat sehubungan dengan angin akan menjadi barat laut (tidak harus 26.6).

Dapat melayani Anda: Teorema Bernoulli

Oleh Teorema Pythagoras:

v _Pada = (240 ²- 120²)^1/2 km/h = 207.8 km/jam

α = arctg (v _V/t / v _Pada ) = arctg (120/207.8) = ke -30 barat laut

-Latihan diselesaikan 3

Seseorang membutuhkan waktu 2 menit untuk berjalan menuruni tangga mekanik yang tidak bergerak. Jika tangga bekerja, orang tersebut membutuhkan waktu 1 menit untuk turun menjadi diam. Berapa lama orang yang berjalan -jalan dan dengan tangga berjalan?

Larutan

Ada tiga elemen yang perlu dipertimbangkan: orang (P), tangga (E) dan tanah, yang kecepatan relatifnya adalah:

v_Pe : kecepatan orang yang sehubungan dengan tangga; v_ADALAH: kecepatan tangga sehubungan dengan tanah; v_P/s: Kecepatan orang sehubungan dengan tanah.

Seperti yang terlihat dari tanah oleh pengamat tetap, orang yang menurunkan tangga (e) memiliki kecepatan v _P/s diberikan oleh:

v _P/s = v_Pe + v_ADALAH

Perasaan positif sedang menuruni tangga. Menjadi T  waktu yang dibutuhkan untuk berjalan dan L jarak. Besarnya orang V _P/s adalah:

v_P/s = L / t

T₁ Ini adalah waktu yang dibutuhkan untuk turun berjalan dengan tangga yang berhenti: v _Pe = L / t₁

Dan T₂ Yang membawa Anda masih turun di tangga bergerak: v _ADALAH = L / t₂

Menggabungkan Ekspresi:

L / t = l / t₁ + L / t₂

Mengganti nilai numerik dan kliring T:

1 / t = 1 / t₁ + 1 / t₂ = 1/2 + 1/1 = 1.5

Lalu t = 1/1.5 menit = 40 detik.

Referensi

1. Bauer, w. 2011. Fisika untuk Teknik dan Ilmu Pengetahuan. Volume 1. MC Graw Hill. 84-88.
2. Figueroa, d. Seri Fisik untuk Sains dan Teknik. Volume 3. Edisi. Kinematika. 199-232.
3. Giancoli, d.  2006. Fisika: Prinsip dengan aplikasi. 6^th. Ed. Prentice Hall. 62-64.
4. Gerakan relatif. Pulih dari: kursus.Lumenarning.com
5. Wilson, J. 2011. Fisika 10. Pendidikan Pearson. 166-168.