Properti bilangan kompleks, contoh, operasi

Itu bilangan kompleks Mereka adalah himpunan numerik yang mencakup bilangan real dan semua akar polinomial, termasuk akar genap dari angka negatif. Akar -akar ini tidak ada dalam set bilangan real, tetapi dalam bilangan kompleks adalah solusinya.

Sejumlah kompleks terdiri dari bagian nyata dan yang lain yang disebut "imajiner". Bagian sebenarnya disebut ke, Misalnya, dan bagian imajiner IB, dengan ke Dan B bilangan real dan "saya" menyukai Unit imajiner. Dengan cara ini bilangan kompleks mengambil formulir:

Z = a + ib

Gambar 1.- Representasi binomial dari bilangan kompleks dalam hal bagian nyata dan bagian imajiner. Sumber: Pixabay.

Contoh bilangan kompleks adalah 2 - 3i, -πi, 1 + (1/2) i. Tapi sebelum beroperasi dengan mereka, mari kita lihat dari mana unit imajiner berasal yo, Mempertimbangkan persamaan kuadrat ini:

X² - 10x + 34 = 0

Di mana a = 1, b = -10 dan c = 34.

Ketika rumus pelarut diterapkan untuk menentukan solusinya, kami menemukan yang berikut:

Bagaimana menentukan nilai √-36? Tidak ada bilangan real bahwa kuadrat adalah jumlah negatif. Maka disimpulkan bahwa persamaan ini tidak memiliki solusi nyata.

Namun, kita bisa menulis ini:

√-36 = √-6² = √6² (-1) = 6√-1

Jika kita mendefinisikan nilai tertentu X seperti yang:

X² = -1

Jadi:

x = ± √-1

Dan persamaan sebelumnya akan memiliki solusi. Oleh karena itu, unit imajiner didefinisikan sebagai:

I = √-1

Dan sebagainya:

√-36 = 6i

Banyak ahli matematika kuno yang bekerja untuk memecahkan masalah serupa, menyoroti Renaissance Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) dan Raffaele Bombelli (1526-1572).

Bertahun-tahun kemudian René Descartes (1596-1650) disebut "imajiner" dengan jumlah seperti √-36 dari contoh. Untuk alasan ini, √-1 dikenal sebagai Unit imajiner.

[TOC]

Properti bilangan kompleks

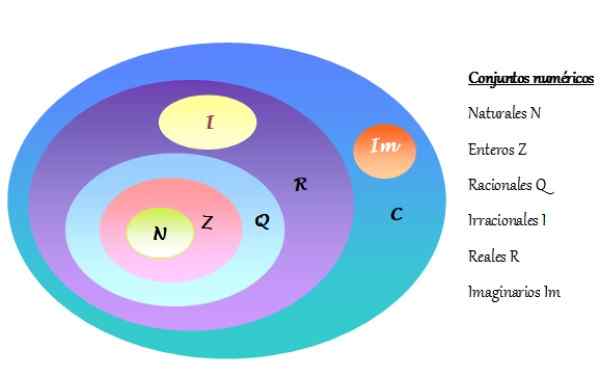
-Himpunan bilangan kompleks dilambangkan sebagai C dan termasuk bilangan real R dan bilangan imajiner IM. Set numerik diwakili dalam diagram Venn, seperti yang ditunjukkan pada gambar berikut:

Dapat melayani Anda: latihan faktorisasi terselesaikan Gambar 2. Venn Diagram set numerik. Sumber: f. Zapata.

-Setiap bilangan kompleks terdiri dari satu bagian nyata dan bagian imajiner lainnya.

-Ketika bagian imajiner dari bilangan kompleks adalah 0, itu adalah bilangan real murni.

-Jika bagian nyata dari bilangan kompleks adalah 0, maka angkanya adalah imajiner murni.

-Dua bilangan kompleks sama jika bagian nyata dan bagian imajiner masing -masing adalah sama.

-Dengan bilangan kompleks, operasi jumlah, pengurangan, perkalian, produk, dan pemberdayaan yang diketahui dilakukan, menghasilkan bilangan kompleks lainnya.

Representasi bilangan kompleks

Bilangan kompleks dapat diwakili dengan berbagai cara. Inilah yang utama:

- Bentuk binomik

Itu adalah bentuk yang diberikan di awal, di mana z adalah bilangan kompleks, ke adalah bagian sebenarnya, B adalah bagian imajiner dan yo Ini adalah unit imajiner:

Z = a + ib

Atau juga:

Z = x + iy

Salah satu cara untuk membuat grafik bilangan kompleks adalah melalui bidang kompleks yang ditunjukkan pada gambar ini. Sumbu imajiner adalah vertikal, sedangkan sumbu asli horizontal dan menunjukkan sebagai RE.

Angka kompleks z Itu diwakili dalam bidang ini sebagai titik koordinat (X, y) salah satu (A, b), seperti yang dilakukan dengan titik -titik pesawat asli.

Jarak dari asal ke titik z adalah modul dari bilangan kompleks, dilambangkan sebagai R, sedangkan φ adalah sudut yang terbentuk R Dengan sumbu asli.

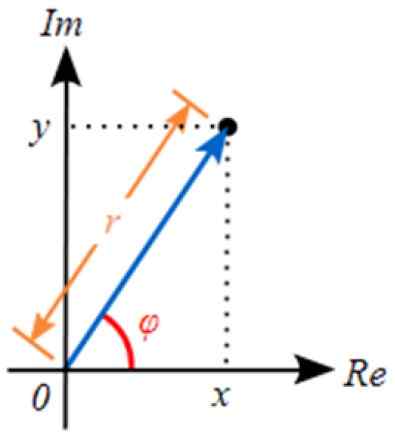
Gambar 3. Representasi bilangan kompleks di bidang kompleks. Sumber: Wikimedia Commons.

Representasi ini terkait erat dengan vektor di bidang nyata. Nilai r sesuai modul dari bilangan kompleks.

Itu dapat melayani Anda: Metode Gauss-Seidel: Penjelasan, Aplikasi, Contoh

- Bentuk kutub

Bentuk kutub terdiri dalam mengekspresikan bilangan kompleks yang memberikan nilai -nilai R dan dari φ. Jika kita melihat angka itu, nilainya R Itu sesuai dengan hipotenuse dari segitiga kanan. Kategorinya Layak ke Dan B, O baik X Dan Dan.

Dalam bentuk binomial atau binomial, kita dapat beralih ke bentuk kutub dengan:

R = √x²+Dan²

Sudut φ Itu adalah yang membentuk segmen R dengan sumbu horizontal atau sumbu imajiner. Itu dikenal sebagai argumen dari bilangan kompleks. Cara ini:

φ = arctg (y/x)

Argumen memiliki nilai -nilai tak terbatas, dengan mempertimbangkan bahwa setiap kali pengembalian diputar, yang bernilai 2π radianes, r sekali lagi menempati posisi yang sama. Dengan cara ini secara umum, argumen z, dilambangkan arg (z), dinyatakan sebagai berikut:

Arg (z) = φ + 2kπ

Di mana k utuh dan berfungsi untuk menunjukkan jumlah belokan yang berbalik: 2, 3, 4 .. . Tanda menunjukkan makna rotasi, jika waktu atau antihorario dibuat.

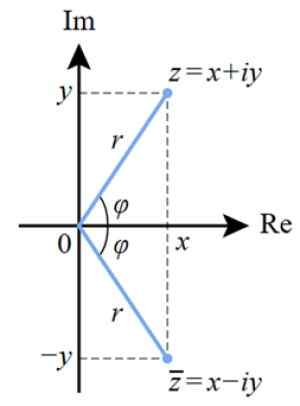
Gambar 4. Representasi kutub dari bilangan kompleks di bidang kompleks. Sumber: Wikimedia Commons.

Dan jika kita ingin meneruskan bentuk kutub ke bentuk binomial, kita menggunakan alasan trigonometri. Dari gambar sebelumnya kita bisa melihat itu:

x = r cos φ

y = r sen φ

Dengan cara ini z = r (cos φ+i sin φ)

Yang disingkat seperti ini:

z = r cis φ

Contoh bilangan kompleks

Angka -bilangan kompleks berikut diberikan secara binomial:

a) 3 + i

b) 4

d) -6i

Dan ini dalam torsi tertib:

a) (-5, -3)

b) (0, 9)

c) (7.0)

Akhirnya, kelompok ini diberikan kutub atau trigonometri:

a) √2 cis 45º

b) √3 cis 30º

Dapat melayani Anda: Distribusi Hypergeometrik: Rumus, Persamaan, Model

c) 2 cis 315º

Untuk apa mereka?

Kegunaan bilangan kompleks melampaui resolusi persamaan tingkat kedua yang ditunjukkan pada awalnya, karena mereka sangat penting dalam bidang teknik dan fisika, terutama dalam:

-Studi gelombang elektromagnetik

-Analisis arus dan tegangan alternatif

-Pemodelan semua jenis sinyal

-Teori relativitas, di mana waktu diasumsikan sebagai besarnya imajiner.

Operasi dengan bilangan kompleks

Dengan bilangan kompleks kita dapat melakukan semua operasi yang dilakukan dengan yang nyata. Beberapa lebih mudah dilakukan jika angkanya datang secara binomis, seperti jumlah dan pengurangan. Di sisi lain, perkalian dan pembagian lebih sederhana jika dilakukan dengan bentuk kutub.

Mari kita lihat beberapa contoh:

- Contoh 1

Tambahkan z₁ = 2 + 5i dan z₂ = -3 -8i

Larutan

Bagian nyata ditambahkan secara terpisah dari bagian imajiner:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Contoh 2

Gandakan z₁ = 4 cis 45º dan z₂ = 5 cis 120º

Larutan

Dapat ditunjukkan bahwa produk dari dua bilangan kompleks dalam kutub atau trigonometri diberikan oleh:

z₁ . z₂ = r₁.R₂ Cis (φ₁ + φ₂)

Menurut Ini:

z₁ . z₂ = (4 × 5) CIS (45 + 120) = 20 cis 165º

Aplikasi

Aplikasi sederhana bilangan kompleks adalah menemukan semua akar persamaan polinomial seperti yang ditunjukkan di awal artikel.

Dalam kasus persamaan x² - 10x + 34 = 0, saat menerapkan rumus pelarut itu diperoleh:

Oleh karena itu solusinya adalah:

X₁ = 5 + 3i

X₂ = 5 - 3i

Referensi

1. Earl, r. Bilangan kompleks. Pulih dari: matematika.sapi.Ac.Inggris.
2. Figuera, J. 2000. Matematika 1. Diversifikasi. Edisi Co-Bo.
3. Hoffmann, J. 2005. Pemilihan masalah matematika. Publikasi Monfort.
4. Jiménez, r. 2008. Aljabar. Prentice Hall.
5. Wikipedia. Bilangan kompleks. Diperoleh dari: di.Wikipedia.org