Bilangan prima yang khas, contoh, latihan

Itu bilangan prima, juga disebut sepupu absolut, adalah bilangan alami yang hanya dapat dibagi satu sama lain dan 1. Dalam kategori ini, angka seperti: 2, 3, 5, 7, 11, 13, 17, 19, 23 dan banyak lagi yang datang dalam kategori ini.

Di sisi lain, nomor majemuk dapat dibagi dengan sendirinya, dengan 1 dan setidaknya satu angka lagi. Kami memiliki contoh pada 12, yang dapat dibagi dengan 1, 2, 4, 6 dan 12. Dengan konvensi, 1 tidak termasuk dalam daftar bilangan prima atau di senyawa.

Gambar 1. Beberapa bilangan prima. Sumber: Wikimedia Commons.

Pengetahuan tentang bilangan prima berasal dari waktu yang jauh; Orang Mesir kuno sudah menangani mereka dan pasti dikenal jauh sebelumnya.

Angka -angka ini sangat penting, karena angka alami apa pun dapat diwakili oleh produk bilangan prima, menjadi representasi unik ini, kecuali dalam urutan faktor -faktor.

Fakta ini sepenuhnya mapan dalam teorema yang disebut Teorema mendasar aritmatika, yang menyatakan bahwa angka -angka yang bukan sepupu harus terdiri dari produk bilangan.

[TOC]

Karakteristik bilangan prima

Di bawah karakteristik utama bilangan prima:

-Mereka tidak terbatas, karena betapapun besar bilangan prima selalu dapat ditemukan.

-Jika bilangan prima P tidak membagi dengan tepat ke nomor lain ke, Kemudian dikatakan itu P Dan ke Mereka adalah sepupu satu sama lain. Ketika ini terjadi, satu -satunya pembagi umum keduanya adalah 1.

Itu tidak perlu ke Jadilah sepupu mutlak. Sebagai contoh, 5 adalah sepupu, dan meskipun 12 tidak, kedua angka adalah sepupu satu sama lain, karena keduanya memiliki pembagi yang sama untuk 1.

-Saat bilangan prima P Bagilah kekuatan angka N, Itu juga membagi a N. Pertimbangkan 100, yang merupakan kekuatan 10, khususnya 10². Kebetulan 2 membagi 100 dan 10.

-Semua bilangan prima ganjil kecuali untuk 2, oleh karena itu digit terakhir mereka adalah 1, 3, 7 atau 9. 5 tidak termasuk, karena meskipun aneh dan sepupu, itu tidak pernah menjadi angka akhir dari bilangan prima lainnya. Faktanya semua angka yang diakhiri dengan 5 adalah kelipatan dari ini dan karenanya bukan sepupu.

Dapat melayani Anda: Simetri Tengah: Properti, Contoh dan Latihan

-Ya P Itu adalah sepupu dan pembagi produk dari dua angka ke.B, Jadi P Bagilah salah satunya. Misalnya, bilangan prima 3 membagi produk 9 x 11 = 99, karena 3 adalah pembagi 9.

Bagaimana mengetahui apakah angka adalah sepupu

Itu Primalitas Itu adalah nama yang diberikan untuk kualitas menjadi sepupu. Nah, matematika Prancis Teorema Kecil Fermat, Yang mengatakan begitu:

"Diberi nomor alami sepupu P dan angka alami ke lebih besar dari 0, itu terpenuhi ke^P - ke Itu adalah kelipatan P, selama P jadilah sepupu ".

Kita dapat menguatkan ini menggunakan jumlah kecil, misalnya misalnya P = 4, Bahwa kita sudah tahu bahwa itu bukan sepupu dan A = 6:

6⁴ - 6 = 1296 - 6 = 1290

Angka 1290 tidak benar -benar dapat dibagi antara 4, oleh karena itu 4 bukan bilangan prima.

Mari kita tes sekarang dengan p = 5, yang sepupu dan A = 6:

6⁵ - 6 = 7766 - 6 = 7760

7760 dapat dibagi antara 5, karena angka apa pun yang berakhir pada 0 atau 5 adalah. Faktanya 7760/5 = 1554. Saat teorema kecil Fermat terpenuhi, kami dapat memastikan bahwa 5 adalah bilangan prima.

Tes melalui teorema efektif dan langsung dengan jumlah kecil, di mana operasi mudah dilakukan, tetapi apa yang harus dilakukan jika mereka meminta kita untuk mengetahui primalitas sejumlah besar?

Dalam hal ini, jumlahnya secara berturut -turut dibagi antara semua bilangan prima kecil, sampai beberapa divisi yang tepat atau bahwa hasil bagi kurang dari pembagi.

Jika ada divisi yang tepat, itu berarti bahwa jumlahnya adalah majemuk dan jika hasil bagi kurang dari pembagi, itu berarti bahwa jumlahnya adalah sepupu. Kami akan mempraktikkannya di tahun diselesaikan 2.

Cara untuk menemukan bilangan prima

Ada bilangan prima tak terbatas dan tidak ada formula unik untuk menentukannya. Namun, mengamati beberapa bilangan prima seperti ini:

Dapat melayani Anda: sudut nol: definisi dan karakteristik, contoh, latihan

3, 7, 31, 127 ..

Diamati bahwa mereka ada dalam bentuk 2^N - 1, dengan n = 2, 3, 5, 7, 9 ... kami meyakinkan Anda:

2² - 1 = 4 - 1 = 3; 2³ - 1 = 8 - 1 = 7; 2⁵ - 1 = 32 - 1 = 31; 2⁷ - 1 = 128 - 1 = 127

Tetapi kami tidak dapat meyakinkan bahwa secara umum 2^N - 1 menjadi sepupu, karena ada beberapa nilai N yang tidak berfungsi, misalnya pada 4:

2⁴ - 1 = 16 - 1 = 15

Dan nomor 15 bukan sepupu, karena berakhir dengan 5. Namun, salah satu bilangan prima terbesar yang diketahui, ditemukan oleh perhitungan komputer, ada di Formulir 2^N - 1 dengan:

N = 57.885.161

Itu Formula Mersenne meyakinkan kita bahwa 2^P - 1 selalu sepupu, selama P Jadilah sepupu juga. Misalnya, 31 adalah sepupu, jadi dapat dipastikan bahwa 2³¹ - 1 Itu juga:

2³¹ - 1 = 2.147.483.647

Namun, rumus hanya memungkinkan beberapa bilangan prima untuk ditentukan, tidak semua.

Formula Euler

Polinomial berikut memungkinkan untuk menemukan bilangan prima selama n adalah antara 0 dan 39:

P (n) = n² + N + 41

Kemudian, di bagian latihan terpecahkan ada contoh penggunaannya.

Pemutaran eratosten

Eratóstenes adalah fisik dan matematika Yunani kuno yang hidup pada abad ketiga hingga.C. Dia merancang metode grafis untuk menemukan bilangan prima yang dapat kita praktikkan dengan angka kecil, itu disebut layar Eratóstenes (layar seperti saringan).

-Angka -angka ditempatkan di tabel seperti yang ditunjukkan dalam animasi.

-Maka angka genap diberi label, kecuali 2 yang kita tahu adalah sepupu. Semua yang lain adalah kelipatan dari ini dan oleh karena itu mereka bukan sepupu.

-Kelipatan 3, 5, 7 dan 11 juga ditandai, tidak termasuk mereka semua karena kita tahu mereka adalah sepupu.

-Kelipatan 4, 6, 8, 9 dan 10 sudah ditandai, karena mereka adalah senyawa dan oleh karena itu kelipatan dari salah satu sepupu yang ditunjukkan.

Dapat melayani Anda: Sejarah Trigonometri dari Asalnya

-Akhirnya, angka yang tersisa tidak ditandai adalah sepupu.

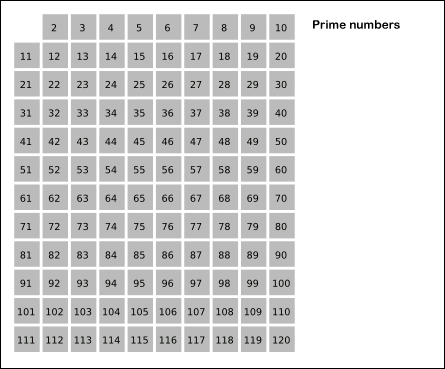Gambar 2. Animasi pemutaran eratostenes. Sumber: Wikimedia Commons.

Latihan

- Latihan 1

Menggunakan polinomial Euler untuk bilangan prima, temukan 3 angka lebih besar dari 100.

Larutan

Ini adalah polinomial yang diusulkan Euler untuk menemukan bilangan prima, yang beroperasi untuk nilai n antara 0 dan 39.

P (n) = n² + N + 41

Melalui Tanteo kita memilih nilai n, misalnya n = 8:

P (8) = 8² + 8 + 41 = 113

Karena n = 8 menghasilkan bilangan prima lebih besar dari 100, maka kami mengevaluasi polinomial untuk n = 9 dan n = 10:

P (9) = 9² + 9 + 41 = 131

P (10) = 10² + 10 + 41 = 151

- Latihan 2

Cari tahu apakah angka -angka berikut adalah sepupu:

a) 13

b) 191

Solusi untuk

13 cukup kecil untuk menggunakan teorema kecil Fermat dan bantuan kalkulator.

Kami menggunakan A = 2 sehingga angkanya tidak terlalu besar, meskipun mereka juga dapat digunakan a = 3, 4 atau 5:

2¹³ - 2 = 8190

8190 dapat dibagi antara 2, karena itu bahkan, oleh karena itu 13 adalah sepupu. Pembaca dapat menguatkannya dengan melakukan tes yang sama dengan A = 3.

Solusi b

191 sangat besar untuk mencoba teorema dan kalkulator umum, tetapi kami dapat menjauhkan pembagian antara setiap bilangan prima. Kami menghilangkan untuk membagi dengan 2 karena 191 tidak rata dan divisi tidak akan tepat atau rasio kurang dari 2.

Kami mencoba membagi dengan 3:

191/3 = 63.666…

Dan itu tidak memberikan yang tepat, atau hasil bagi kurang dari pembagi (63.666 ... lebih besar dari 3)

Kami terus menguji 191 oleh sepupu 5, 7, 11, 13 dan divisi yang tepat tidak tercapai, atau rasionya kurang dari pembagi. Sampai terbelah antara 17:

191/17 = 11, 2352 ..

Karena tidak tepat dan 11.2352 ... kurang dari 17, nomor 191 adalah sepupu.

Referensi

1. Baldor, a. 1986. Hitung. Edisi dan distribusi Codex.
2. Prieto, c. Angka primo. Diperoleh dari: halaman.Matem.Unam.MX.
3. Sifat bilangan prima. Pulih dari: mae.UFL.Edu.
4. Smartick. Angka Primo: Cara Menemukan Mereka Dengan Saringan Eratostenes. Pulih dari: smartick.adalah.
5. Wikipedia. bilangan prima. Pulih dari: is.Wikipedia.org.