Properti, Contoh dan Operasi Bilangan Rasional

Itu angka rasional Mereka semua adalah angka yang dapat diperoleh sebagai pembagian dua bilangan bulat. Contoh bilangan rasional adalah: 3/4, 8/5, -16/3 dan yang muncul dalam gambar berikut. Dalam bilangan rasional, hasil bagi ditunjukkan, dimungkinkan untuk melakukannya nanti jika diperlukan.

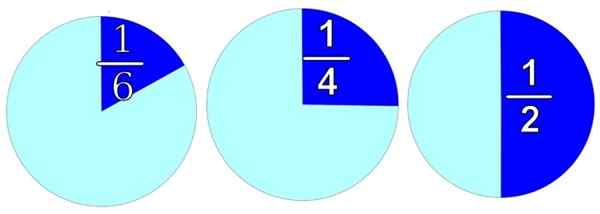
Dalam gambar apa pun objek diwakili, bulat untuk kenyamanan. Jika kita ingin membaginya menjadi 2 bagian yang sama, seperti di sebelah kanan, kita memiliki dua bagian dan masing -masing 1/2.

Gambar 1. Bilangan rasional digunakan untuk membagi keseluruhan menjadi berbagai bagian. Sumber: Freesvg.

Dengan membaginya menjadi 4 bagian yang sama, kami akan memperoleh 4 bagian dan masing -masing bernilai 1/4, seperti pada gambar pusat. Dan jika Anda harus mendistribusikannya dalam 6 bagian yang sama, maka setiap bagian akan bernilai 1/6, yang kita lihat pada gambar di sebelah kiri.

Tentu saja, kita juga bisa membaginya menjadi dua bagian yang tidak sama, misalnya kita bisa menyimpan 3/4 bagian dan menyimpan 1/4 bagian. Divisi lain juga dimungkinkan, seperti 4/6 bagian dan 2 bagian. Yang penting adalah jumlah dari semua bagian adalah 1.

Dengan cara ini, terbukti bahwa dengan bilangan rasional Anda dapat membagi, menghitung dan mendistribusikan hal -hal seperti makanan, uang, tanah, dan semua jenis benda dalam pecahan. Jadi jumlah operasi yang dapat dilakukan dengan angka diperpanjang.

Bilangan rasional juga dapat diungkapkan secara desimal, seperti yang dapat dilihat dalam contoh -contoh berikut:

1/2 = 0,5

1/3 = 0.3333…

3/4 = 0,75

1/7 = 0.142857142857142857…

Kemudian kami menunjukkan bagaimana berpindah dari satu cara ke jalan lain dengan contoh.

[TOC]

Properti bilangan rasional

Nomor rasional, yang set yang akan kami tunjukkan dengan huruf Q, memiliki properti berikut:

-Q Termasuk bilangan alami n dan seluruh angka n.

Dengan mempertimbangkan nomor apa pun ke Ini dapat dinyatakan sebagai hasil bagi satu sama lain dan 1, mudah untuk melihat bahwa ada juga bilangan alami dan bilangan bulat.

Dengan demikian, bilangan alami 3 dapat ditulis sebagai fraksi, dan juga -5:

3 = 3/1

-5 = -5/1 = 5/-1 = -(5/1)

Dengan cara ini itu adalah set numerik yang mencakup sejumlah lebih banyak angka, sesuatu yang sangat diperlukan, letakkan angka "bundar" tidak cukup untuk menggambarkan semua operasi yang mungkin untuk dilakukan.

Dapat melayani Anda: 90 pembagi: Apa itu dan penjelasan

-Bilangan rasional dapat ditambahkan, dikurangi, mengalikan dan membagi, hasil operasi menjadi bilangan rasional: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.

-Di antara setiap pasangan bilangan rasional, bilangan rasional lain selalu dapat ditemukan. Faktanya, antara dua bilangan rasional ada rasional tak terbatas. 

Misalnya, antara 1/4 dan 1/2 rasional adalah rasional 3/10, 7/20, 2/5 (dan banyak lagi), yang dapat diverifikasi mengekspresikannya sebagai desimal.

-Bilangan rasional apa pun dapat dinyatakan sebagai: i) bilangan bulat atau ii) desimal terbatas (ketat) atau koran: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,1666666…

-Jumlah yang sama dapat diwakili oleh fraksi setara yang tak terbatas dan semuanya milik Q. Mari kita lihat grup ini:

Semua mewakili desimal 0.428571 ..

-Di antara semua fraksi setara yang mewakili jumlah yang sama, fraksi yang tidak dapat direduksi, yang paling sederhana dari semuanya, adalah Perwakilan kanonik dari angka itu. Perwakilan kanonik dari contoh sebelumnya adalah 3/7.

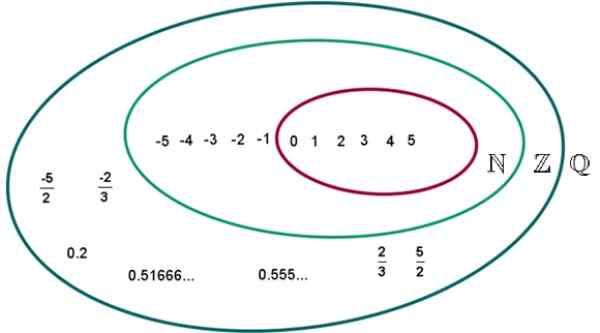Gambar 2.- Set q bilangan rasional. Sumber: Wikimedia Commons. UVM Eduardo Artur/CC BYS-S (https: // CreativeCommons.Org/lisensi/by-sa/4.0).

Contoh bilangan rasional

-Pecahan sendiri, yang di mana pembilang kurang dari penyebut:

-Fraksi yang tidak tepat, yang pembilangnya lebih besar dari penyebut:

-Bilangan alami dan bilangan bulat:

-Fraksi yang setara:

Representasi desimal dari bilangan rasional

Ketika pembilang dibagi antara penyebut adalah bentuk desimal dari bilangan rasional. Misalnya:

2/5 = 0.4

3/8 = 0.375

1/9 = 0.11111 ..

6/11 = 0.545454…

Dalam dua contoh pertama, jumlah desimal terbatas. Ini berarti bahwa ketika divisi dibuat, istirahat diperoleh.

Di sisi lain, di dua berikutnya, jumlah desimal tidak terbatas dan itulah sebabnya poin suspensi ditempatkan. Dalam kasus terakhir ada pola dalam desimal. Dalam kasus fraksi 1/9 Gambar 1 diulangi tanpa batas waktu, sedangkan di 6/11 adalah 54.

Itu dapat melayani Anda: probabilitas frekuensi: konsep, bagaimana itu dihitung dan contoh

Ketika ini terjadi dikatakan bahwa desimal adalah koran dan dilambangkan dengan aksen sirkumflex sebagai berikut:

Mengubah desimal menjadi pecahan

Jika itu adalah desimal yang terbatas, koma hanya dihilangkan dan penyebut menjadi unit diikuti oleh sebanyak nol dan angka memiliki desimal. Misalnya, untuk mengubah desimal 1.26 Dalam fraksi ditulis seperti ini:

1.26 = 126/100

Maka fraksi yang dihasilkan disederhanakan hingga maksimal:

126/100 = 63/50

Jika desimal tidak terbatas pertama periode diidentifikasi. Kemudian langkah -langkah ini diikuti untuk menemukan fraksi yang dihasilkan:

-Pembilang adalah pengurangan antara angka (tidak ada koma atau aksen sirkumfleks) dan bagian yang tidak membawa aksen sirkumfleks.

-Denominator adalah bilangan bulat dengan sebanyak 9 angka di bawah sirkumfleks, dan sebanyak atau sebagai angka di bagian desimal mereka tidak berada di bawah sirkumfleks.

Mari ikuti prosedur ini untuk mengubah bilangan desimal 0.428428428… dalam fraksi.

-Pertama periode diidentifikasi, yang merupakan urutan yang diulang: 428.

-Kemudian operasi mengurangi angka tanpa koma atau aksen dilakukan: 0428 dari bagian yang tidak memiliki sirkumfleks, yaitu 0. Ini adalah 428 - 0 = 428.

-Denominator dibangun, mengetahui bahwa di bawah sirkumfleks ada 3 angka dan semuanya berada di bawah sirkumfleks. Oleh karena itu penyebutnya adalah 999.

-Akhirnya fraksi terbentuk dan disederhanakan jika memungkinkan:

0.428 = 428/999

Tidak mungkin lebih menyederhanakan.

Operasi bilangan rasional

- Tambahkan dan Kurangi

Pecahan dengan penyebut yang sama

Ketika fraksi memiliki denominator yang sama, tambahkan dan/atau kurangi mereka sangat mudah, karena pembilang hanya ditambahkan secara aljabar, pergi sebagai penyebut hasil yang sama dari penambahan yang sama. Akhirnya, jika memungkinkan, itu disederhanakan.

Contoh

Melakukan jumlah aljabar berikut dan menyederhanakan hasilnya:

Fraksi yang dihasilkan sudah tidak dapat direduksi.

Pecahan dengan denominator yang berbeda

Dalam hal ini, addor digantikan oleh fraksi yang setara dengan denominator yang sama dan kemudian prosedur sudah dijelaskan. 

Contoh

Secara aljabar menambahkan bilangan rasional berikut yang menyederhanakan hasilnya:

Dapat melayani Anda: tepi kubus

Langkahnya adalah:

-Tentukan ganda umum minimum (MCM) dari penyebut 5, 8 dan 3:

MCM (5,8,3) = 120

Ini akan menjadi penyebut fraksi yang dihasilkan tanpa menyederhanakan.

-Untuk setiap fraksi: Bagilah MCM antara penyebut dan kalikan dengan pembilang. Hasil operasi ini ditempatkan, dengan tanda masing -masing, di pembilang fraksi. Dengan cara ini fraksi yang setara dengan aslinya diperoleh, tetapi dengan MCM sebagai penyebut.

Misalnya, untuk fraksi pertama, pembilang dibangun seperti ini: (120/5) x 4 = 96 dan diperoleh:

Lanjutkan dengan cara yang sama untuk fraksi yang tersisa:

Akhirnya, fraksi yang setara diganti tanpa melupakan tanda mereka dan jumlah aljabar dari pembilang dibuat:

(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =

= (96+210-440+24) / 120 = -110 / 120 = -11/12

- Penggandaan dan Divisi

Multiplikasi dan Divisi dilakukan mengikuti aturan yang ditunjukkan di bawah ini:

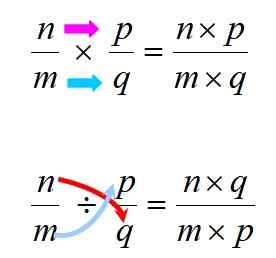Gambar 3. Aturan untuk melaksanakan perkalian dan pembagian bilangan rasional. Sumber: f. Zapata.

Bagaimanapun, penting untuk diingat bahwa perkalian adalah komutatif, yang berarti bahwa urutan faktor tidak mengubah produk. Ini tidak terjadi dengan divisi, jadi Anda harus berhati -hati untuk menghormati urutan antara dividen dan pembagi.

Contoh 1

Lakukan operasi berikut dan sederhanakan hasilnya:

a) (5/3) x (8/15)

b) (-4/5) ÷ (2/9)

Menjawab

(5/3) x (8/15) = (5 x 8)/(3 x 15) = 15/120 = 1/8

Jawaban b

(-4/5) ÷ (2/9) = (-4 x 9)/(5 x 2) = -36/10 = -18/5

Contoh 2     

Luisa punya $ 45. Dia menghabiskan sepersepuluh membeli buku dan 2/5 bagian dari apa yang tersisa di kemeja. Berapa banyak uang yang tersisa Luisa? Ekspresikan hasil dalam fraksi yang tidak dapat direduksi.

Larutan

Biaya buku (1/10) x 45 $ = 0.1 x 45 $ = 4.5 $

Oleh karena itu Luisa tetap dengan:

45 - 4.5 $ = 40.5 $

Dengan uang itu, Luisa pergi ke toko pakaian dan membeli kemeja itu, yang harganya:

(2/5) x 40.5 $ = 16.2 $

Sekarang Luisa memiliki dalam portofolio:

40.5 - 16.2 $ = 24.3 $

Untuk mengekspresikannya dalam fraksi, tertulis seperti ini:

24.3 = 243/10

Itu tidak bisa direduksi.

Referensi

1. Baldor, a. 1986. Hitung. Edisi dan distribusi Codex.
2. Carena, m. 2019. Manual Matematika. Universitas Nasional Pantai.
3. Figuera, J. 2000. Matematika 8. Edisi Co-Bo.
4. Jiménez, r. 2008. Aljabar. Prentice Hall.
5. Angka rasional. Pulih dari: cimanet.UOC.Edu.
6. Angka rasional. Diperoleh dari: WebDelProfesor.Ula.pergi.