Matematika

Notasi desimal

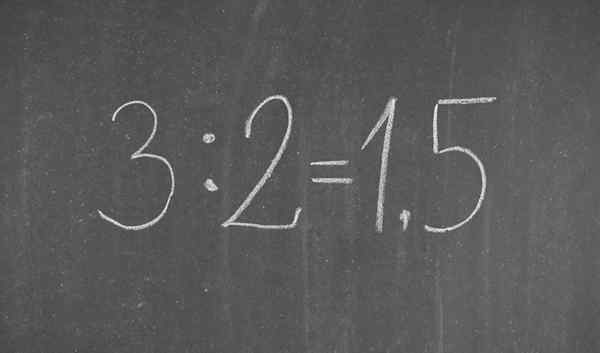
Notasi desimal
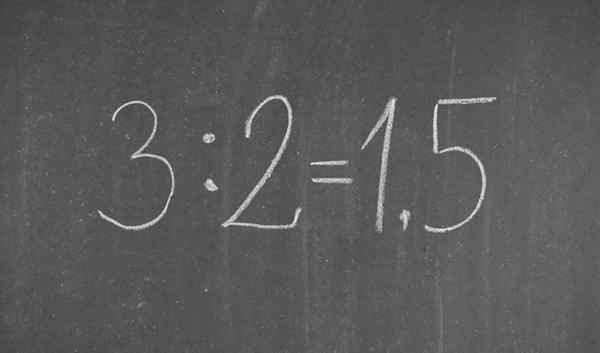Fraksi 3/2 yang ditulis dalam notasi desimal

Apa itu notasi desimal?

Itu notasi desimal Ini terdiri dari menulis bilangan real melalui seluruh bagian dan bagian desimal, baik dipisahkan oleh suatu titik atau koma. Seluruh bagian tersisa dan bagian desimal di sebelah kanan titik itu.

0 dapat muncul baik di seluruh bagian maupun di desimal. Misalnya, angka -angka berikut adalah bilangan desimal:

  • 0.25
  • 1.5903
  • 4.19367

Perhatikan bahwa bagian desimal dari angka -angka ini terbatas, tetapi ada juga angka -angka dengan bagian desimal yang tak terbatas, seperti 0,33333 ..., di mana poin -poin suspensi ditempatkan sebagai cara untuk menunjukkan bahwa jumlah desimal berlanjut tanpa batas waktu tanpa batas waktu tanpa batas waktu tanpa batas waktu tanpa batas waktu.

Secara umum, angka desimal yang terbatas dapat ditulis sebagai:

N.ke1ke2ke3… keN

Menjadi n bilangan bulat dan n jumlah desimal, sedangkan desimal tak terbatas mengadopsi formulir:

N.ke1ke2ke3..

Di desimal 0.25 diidentifikasi:

  • N = 0
  • ke1 = 2
  • ke2 = 5

Desimal muncul sebagai cara lain untuk mengekspresikan bilangan rasional, yang berbentuk atau rusak. Faktanya, fraksi apa pun dapat ditulis dalam notasi desimal, seperti yang akan segera dilihat.

Mereka juga berfungsi untuk mewakili angka yang tidak berasal dari sebagian kecil, yang disebut bilangan irasional, seperti: π, √2, √3, √5, angka "e" dan banyak lainnya.

Contoh bilangan desimal

Jumlah desimal dapat diperoleh dari fraksi dengan cara yang sangat sederhana: menghitung hasil bagi pembilang antara penyebut. Jika penyebutnya adalah unit yang diikuti oleh nol, ini sangat sederhana:

  • 8/10 = 0.8
  • - (5/100) = −0.05

Dalam kasus pertama, karena penyebutnya adalah 10, titik desimal ditempatkan segera di sebelah kiri 8 dan desimal 0.8 membaca "8 persepuluh" atau "nol poin delapan".

Dalam kasus kedua, karena penyebutnya adalah 100, Anda harus menempatkan titik desimal dua tempat di sebelah kiri 5, dan karena angkanya negatif, berbunyi "kurang 5 ratus" atau "kurang nol nol poin lima".

Ketika penyebut bukan unit yang diikuti oleh 0, divisi panjang digunakan:

Perhatikan bahwa untuk melaksanakan divisi ini, karena pembilang kurang dari penyebut, itu dikalikan terlebih dahulu dengan 10 dan dengan melakukan itu, 0 diikuti oleh titik desimal dalam hasil bagi, agar tidak mengubah operasi, agar tidak untuk mengubah operasi. Kemudian lanjutkan secara normal untuk membagi 10 dengan 2 yang sama dengan 5 dan residu divisi adalah 0.

Dapat melayani Anda: jumlah vektor

Bentuk desimal fraksi ½ adalah 0.5, bahwa "titik nol lima" dibaca:

Fraction 7/8 adalah contoh lain. Karena 7 kurang dari 8, dikalikan 7 × 10 = 70, 0 ditempatkan dalam hasil bagi diikuti oleh titik desimal dan biasanya dibagi:

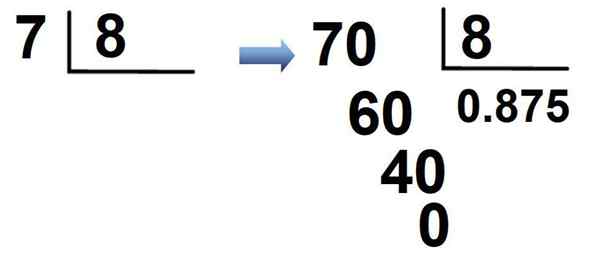
Hasilnya adalah fraksi ditulis dalam notasi desimal sebagai:

7/8 = 0.875

Jumlah ini, seperti hasil sebelumnya, adalah desimal yang terbatas dan cara membacanya adalah: "nol poin delapan ratus tujuh puluh lima". Melalui prosedur ini, fraksi berikut juga ditulis dalam notasi desimal:

8/10 = 0.8

5/7 = 0.714285714…

9/20 = 0.Empat. Lima

3/8 = 0.375

Perhatikan bahwa seperti dalam semua fraksi ini, pembilang kurang dari penyebut, seluruh bagian desimal yang dihasilkan adalah 0. Namun, angka campuran atau a Fraksi yang tidak tepat (Yang pembilangnya lebih besar dari penyebutnya) juga memiliki representasi desimal.

Dalam hal ini, seluruh bagian lebih besar dari atau sama dengan 1 jika fraksi positif, dan kurang dari -1 jika negatif:

9/4 = 2.25

10/3 = 3.333333…

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Seluruh bagian dan bagian fraksional dari desimal negatif

Dalam contoh sebelumnya diamati bahwa untuk menemukan ekspresi desimal dari fraksi, pembilang dan penyebut dibagi secara sederhana. Bahkan jika fraksinya negatif, cukup tanda minus dimasukkan ke ekspresi desimien yang setara.

Namun, seluruh bagian dan bagian fraksional dari desimal berbeda sesuai dengan tanda yang Anda bawa.

Saat desimal positif, seperti 2.25, seluruh bagiannya adalah 2 dan bagian desimalnya adalah 0.25 dan jumlahnya dapat ditulis sebagai jumlah seluruh bagian dan bagian desimal, seperti ini:

2.25 = 2 + 0.25

Seluruh bagian didefinisikan sebagai bilangan bulat segera lebih rendah dari desimal dan bagian desimal selalu positif. Untuk 2.25, bilangan bulat yang segera lebih rendah adalah 2.

Tetapi dalam kasus fraksi −12/5, setara dengan desimal −2.4 Di atas tidak berhasil.

Dapat melayani Anda: apa saja bagian dari pesawat Cartesian?

 Jika −2 itu adalah seluruh bagian, dan 0.4 Bagian desimal, dengan menambahkan akan diperoleh:

−2 + 0.4 = −1.6 ≠ −2.4

Oleh karena itu, seluruh bagian −2.4 tidak bisa −2 tetapi bilangan bulat yang segera lebih rendah: −3. Namun dalam hal ini, bagian pecahan tidak akan 0.4, karena dengan menambahkan:

−3 + 0.4 = −2.6 ≠ −2.4

Jadi apa bagian desimal dari angka negatif −2.4? Ini mengurangi angka desimal dari seluruh bagiannya dan hasilnya akan selalu positif:

−2.4 - ( - 3) = 0.6

Akhirnya, terbukti bahwa dengan menambahkan seluruh bagian dan bagian pecahan, desimal yang dicari diperoleh:

−3 + 0.6 = −2.4

Prosedur untuk menemukan bagian dan bagian desimal dari angka apa pun, terlepas dari tandanya, dirangkum dengan cara ini:

  • Seluruh bagian adalah bilangan bulat segera lebih rendah dari angka desimal.
  • Bagian desimal dihitung dengan mengurangi desimal dari seluruh bagiannya.

Namun, untuk tujuan perhitungan praktis, angka desimal −2.4 dapat dipecah sebagai - (2 + 0.4) = - 24/10 atau:

Seperti yang dapat dilihat, representasi notasi desimal dari suatu angka tidak unik.

Jenis desimal

Ada bilangan desimal yang bagian desimalnya terbatas atau tak terbatas, yang digunakan sebagai kriteria klasifikasi:

Desimal yang terbatas atau tepat

Saat desimal terbatas, seperti 0.125, juga dikatakan bahwa mereka desimal yang tepat.

Desimal yang tak terbatas

Desimal yang tak terbatas diperoleh ketika residu pembagian antara pembilang dan penyebut tidak pernah dibuat 0.

Dengan ketentuan bahwa desimal berasal dari hasil bagi antara dua bilangan bulat, bagian desimal ini adalah periodik, yaitu, terdiri dari satu atau beberapa gambar yang diulangi tanpa batas waktu, disebut periode.

Misalnya, nomor 3.333333 ... berasal dari fraksi yang tidak tepat 10/3, itu adalah desimal periodik: seluruh bagian adalah 3, dan setelah titik desimal, angka 3 diulangi tanpa batas waktu. Ini dapat dilambangkan dengan menempatkan kurva atau topi pada nomor yang diulang:

Periode ini bisa menjadi angka yang lebih besar, seperti dalam fraksi 5/7, yang perwakilannya dalam notasi desimal adalah 0.71428571428571428 ... dan ditulis sebagai:

Dapat melayani Anda: variasi proporsional

Desimal -desimal di mana periode ini muncul segera setelah titik desimal disebut Desimal periodik murni. Namun, dalam hal lain ini:

Periode, yaitu 45, didahului oleh dua digit yang tidak diulang lagi di bagian desimal: 23. Angka ini disebut Ante-periode, karena mendahului periode. Dalam hal ini adalah a Campuran surat kabar desimal.

Akhirnya ada desimal tak terbatas yang bukan surat kabar, yang tidak berasal dari hasil bagi antara dua bilangan bulat. Seperti yang disebutkan di awal, desimal ini adalah milik keseluruhan bilangan irasional, Seperti nomor PI, misalnya.

Latihan terpecahkan

Latihan 1

Tulis numerik angka desimal berikut:

a) nol poin empat ratus empat puluh tahun
b) lima ribu
c) dua unit dan lima ratus
D) Tiga Poin Dua Puluh Seven Negatif
e) satu poin delapan ratus dua puluh ribu lima ratus enam puluh tiga

  • Larutan

a) 0.447

b) 0.005

c) 2.05

D) −3.27

e) 1.824563

Latihan 2

Klasifikasi angka desimal berikut dalam desimal yang tepat, surat kabar murni, surat kabar campuran atau bilangan irasional. Dalam semua kasus, tunjukkan nilai seluruh bagian, dan jika mereka adalah surat kabar atau surat kabar campuran, juga menunjukkan nilai periode dan anterior, yang sesuai:

a) 0.35627

b) 1.21212121…

c) −1.32

d) 1.414213562… = √2

  • Larutan

a) 35627 adalah desimal yang tepat. Seluruh bagiannya adalah 0 dan bagian desimalnya adalah 0.35627.

b) 1.21212121… adalah surat kabar desimal dan murni yang tak terbatas, seluruh bagiannya adalah 1 dan periode adalah 21.

c) −1.32 adalah desimal yang tepat dan negatif, yang seluruh bagiannya adalah −2. Bagian desimal dihitung dengan mengurangi angka desimal dari seluruh bagian:

−1.32 - (−2) = 0.68

d) Ekspresi desimal √2 tidak terbatas dan tidak periodik, karena itu adalah bilangan irasional.

Ini adalah koran campuran, seluruh bagiannya adalah 3, anterior adalah 1 dan periode 89.

Referensi

  1. Kontribusi pedagogis dan bahan didaktik. Notasi desimal. Pulih dari: Tecdigital.Tec.Ac.Cr.
  2. Baldor, a. 2007. Aritmatika teoretis praktis. Grup Editorial Patria S.KE. dari c.V.
  3. Matematika untuk perdagangan. Memahami notasi desimal. Diperoleh dari: OpenTextBC.Ac.
  4. Unam. Bilangan Rasional: Makna dan Representasi. Pulih dari: redi.Kodeik.Unam.MX.