Menunggu formula garis dan persamaan, representasi, contoh

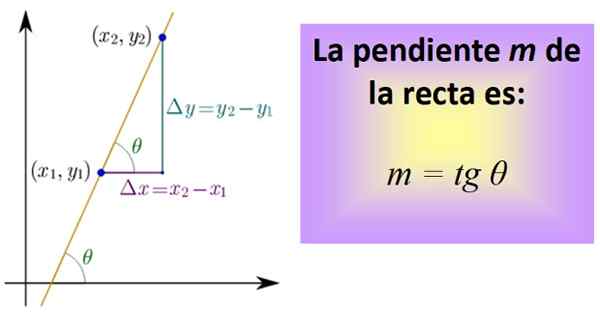
Itu garis yang tertunda Ini adalah garis singgung dari sudut θ bahwa garis ini terbentuk dengan sumbu horizontal, yang oleh konvensi diukur dalam arah yang berlawanan dengan tangan jam. Kemiringan garis apa pun selalu konstan dan itulah sebabnya itu adalah salah satu karakteristik yang paling penting.

Untuk menghitungnya, Anda perlu mengetahui dua titik garis, yang koordinatnya adalah (x x₁,Dan₁) dan (x₂,Dan₂). Di antara kedua titik segmen ditarik milik garis dan kemudian segmen yang mewakili jarak antara x ditarik₁ dan x₂, dan antara dan₁ dan dan₂, Seperti pada gambar yang lebih rendah.

Gambar 1. Kemiringan garis adalah garis singgung sudut θ. Sumber: Wikimedia Commons.

Tiga segmen membentuk segitiga kanan yang kakinya: Δx = x₂ - X₁  dan Δy = dan₂ - Dan₁. Mereka sesuai masing -masing dengan perpindahan horizontal dan vertikal lainnya.

Sekarang hasil bagi didefinisikan, disebut garis singgung sudut θ dan disingkat tg θ, yang justru lereng M dari garis:

m = tg θ = Δy / Δx

Perhatikan bahwa untuk satu garis, sudut ini tetap konstan, terlepas dari titik yang diambil untuk menghitung garis singgungnya. Bagaimanapun, nilai ini menawarkan kepada kita bagaimana cenderung itu adalah garis.

Melalui koordinat titik yang dipilih, formula kemiringan tetap:

M = (y - y₁ ) / (X₂ - X₁)

[TOC]

Representasi Grafis

Di bawah ini kami memiliki beberapa situasi di mana konsep kemiringan relevan. Nilainya dapat dengan mudah dihitung dengan mengukur masing -masing perpindahan vertikal dan horizontal, dan kemudian membuat hasil bagi ditunjukkan pada awal.

Ini memberi kita gambaran tentang lereng atau penurunan beberapa struktur, seperti jalan, atap atau jalan:

Dapat melayani Anda: pengambilan sampel acak: metodologi, kelebihan, kerugian, contoh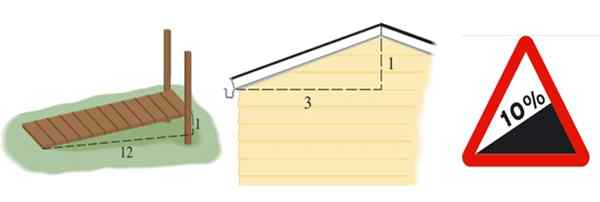 Gambar 2. Dari kiri ke kanan lereng jalan, atap dan lereng jalan, yang terakhir diekspresikan dalam persentase. Sumber: Stewart, J. Precáculculo dan Wikimedia Commons (gambar kanan).

Kemiringan jalan yang ditunjukkan pada Gambar 2 di sebelah kiri adalah M = 1/12, atapnya adalah M = 1/3 dan jalan dinyatakan dalam persentase. Persentase 10 % berarti bahwa untuk setiap 100 meter yang maju secara horizontal, mereka mendapatkan tinggi 10 meter:

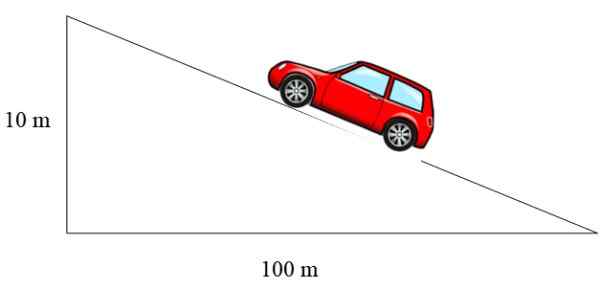Gambar 3. Sebuah kendaraan naik melalui lereng yang kemiringannya 10%. Sumber: f. Zapata.

Dalam hal ini kemiringannya 10/100 = 0.1, yang dinyatakan sebagai persentase sama dengan 10%.

Jenis kemiringan

Kemiringan garis bisa positif, negatif atau nol. Misalnya garis yang ditunjukkan pada Gambar 1 memiliki kemiringan positif. Kami menghargainya segera karena kami melihat bahwa saluran itu "diangkat" jika kami melihatnya dari kiri ke kanan.

Jika garis turun melihatnya dari kiri ke kanan, maka kemiringannya negatif. Dan saat garis horizontal, kemiringannya nol.

Akhirnya, untuk garis vertikal, kemiringan tidak ditentukan.

Representasi grafis dari masing -masing jenis ditemukan di bawah ini:

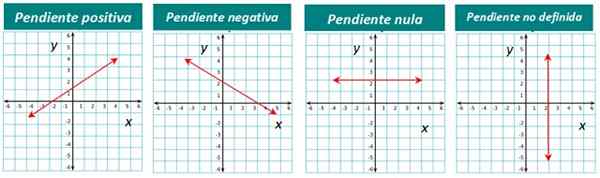Gambar 4. Garis -garis sesuai dengan kemiringan Anda. Sumber: f. Zapata.

Bagaimana lereng dihitung garis?

Menghitung kemiringan sangat sederhana, Anda hanya perlu menemukan perpindahan vertikal dan perpindahan horizontal, dan kemudian buat hasil bagi keduanya.

Saat Anda memiliki gambar garis di bidang Cartesian, perpindahan ini memilih dua titik dari garis p₁ Dan p₂, Menentukan koordinat mereka dan menerapkan definisi yang diberikan di awal:

Dapat melayani Anda: apa yang mewakili panjang perpindahan segi enam

M = (y - y₁ ) / (X₂ - X₁ )

Karena nilai lereng tidak tergantung pada pilihan p₁ Dan p₂ , Kami akan memilih titik P dari koordinat (x, y) yang menjadi milik garis, yang koordinatnya tidak diketahui, dan titik lain p₁ yang koordinatnya adalah: (x₁,Dan₁).

Kemiringannya adalah:

M = (y - y₁) / (x - x₁)

Kami dapat menghapus Dan:

dan dan₁ = m (x - x₁)

Sekarang anggaplah poin p₁ Ini adalah persimpangan garis dengan sumbu vertikal, koordinat (0, b). Mengganti ini dalam persamaan sebelumnya:

dan - b = m (x - 0) → y = mx + b

Ekspresi ini dikenal sebagai persamaan garis dalam bentuk Tertunda - persimpangan, karena garis ditentukan secara tegas ketika kemiringan dan persimpangan dengan sumbu vertikal diketahui.

Mengetahui hanya kemiringannya tidak cukup untuk mengkarakterisasi garis di pesawat, karena Infinite Straight dapat memiliki kemiringan yang sama, yang berarti mereka paralel, tetapi melalui titik -titik lain.

Latihan terpecahkan

- Latihan 1

Temukan kemiringan garis yang ditunjukkan pada gambar berikut:

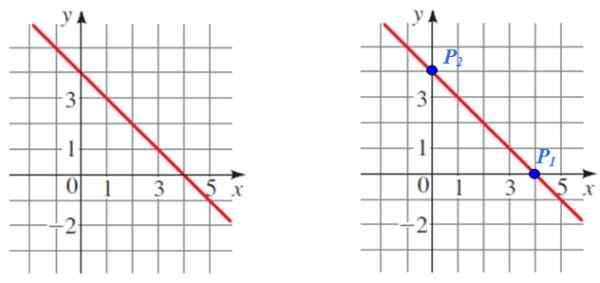Gambar 5. Melalui grafik garis dua titik dipilih untuk menghitung kemiringannya. Sumber: f. Zapata.

Larutan

P₁ Dan p₂ Mereka adalah dua titik mudah -untuk -dibaca yang akan berfungsi untuk perhitungan, juga mencatat bahwa mereka adalah persimpangan masing -masing dengan sumbu koordinat.

Koordinat setiap titik adalah:

P₁ (4.0) dan p₂ (0.4)

Dengan mengganti persamaan lereng:

m = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

Kemiringannya negatif, yang diharapkan setelah mengamati grafik.

Dapat melayani Anda: Nomor kompleks: properti, contoh, operasi

- Latihan 2

Temukan persamaan garis yang melewati titik (1, -6) dan sejajar dengan garis y = 2x - 3.

Larutan

Kemiringan garis yang dicari harus sama dengan Y = 2x - 3, karena mereka paralel. Untuk garis ini kemiringannya adalah M = 2, oleh karena itu yang kami cari memiliki formulir:

dan dan₁ = 2 (x - x₁)

Sekarang kami mengganti titik yang melaluinya garis kami lewat: x₁ = 1 dan₁ = -6.

dan - (-6) = 2 (x - 1)

Oleh karena itu y = 2x - 2 - 6 → y = 2x - 8

Contoh

Dua kuantitas dapat dikaitkan sedemikian rupa sehingga grafik Anda adalah garis lurus. Dalam hal ini dikatakan bahwa jumlah tersebut memiliki ketergantungan linier dan kemiringan garis dapat diartikan sebagai alasan perubahan satu variabel ke yang lain.

Contoh 1

Misalkan kolam diisi dengan air ke a kecepatan konstan dalam waktu. Secara alami, semakin banyak waktu berlalu, semakin banyak air yang disimpan. Nah, laju di mana kumpulan diisi justru kemiringan garis yang menghubungkan volume dengan waktu:

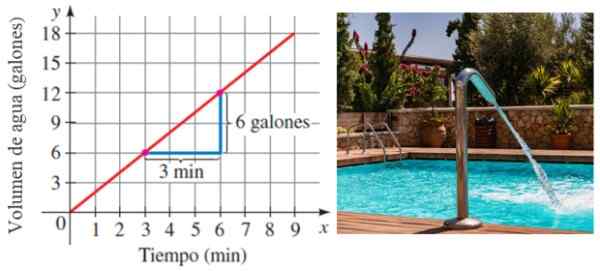Gambar 6. Lereng sebagai alasan perubahan. Sumber: Stewart, J./Pxfuel.

Dalam contoh ini, kolam diisi dengan kecepatan 6/3 galon per menit atau 2 galon/menit.

Contoh 2

Saat ponsel bergerak dalam garis lurus dengan kecepatan konstan, kemiringan grafik posisi tergantung pada waktu tidak lain adalah kecepatan tersebut. Grafik menunjukkan ponsel dengan kecepatan positif, yang berarti bergerak menjauh dari asal.

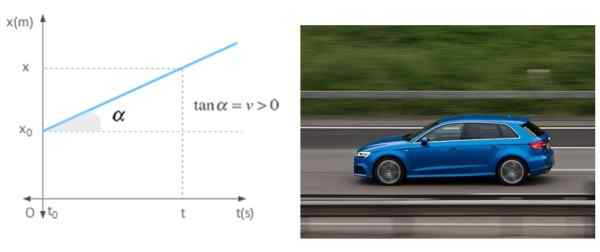Gambar 7. Kemiringan grafik versus waktu adalah kecepatan ponsel dalam gerakan bujursangkar yang seragam. Sumber: Wikimedia Commons/Pixabay.

Referensi

1. Alvarez, J. Kemiringan jalan. Pulih dari: geogebra.adalah.
2. Carena, m. 2019. Manual Matematika Preuniversity. Universitas Nasional Pantai.
3. Hoffman, J. Pemilihan masalah matematika. Volume 4.
4. Jiménez, r. 2008. Aljabar. Prentice Hall.
5. Stewart, J. 2006. PRECCCULMENT: Matematika untuk Perhitungan. Ke -5. Edisi. Pembelajaran Cengage.
6. Zill, d. 1984. Aljabar dan Trigonometri. Bukit McGraw.