Penjelasan Tekanan Manometrik, Rumus, Persamaan, Contoh

Itu pengukur tekanan P_M Ini adalah salah satu yang diukur dalam kaitannya dengan tekanan referensi, yang dalam banyak kasus dipilih sebagai tekanan atmosfer p_ATM di permukaan laut. Itu kemudian a Tekanan relatif, Istilah lain yang juga diketahui.

Cara lain di mana tekanan biasanya diukur membandingkannya dengan kekosongan absolut, yang tekanannya selalu nil. Dalam hal ini ada pembicaraan tentang tekanan mutlak, yang akan kami tunjukkan bagaimana p_ke.

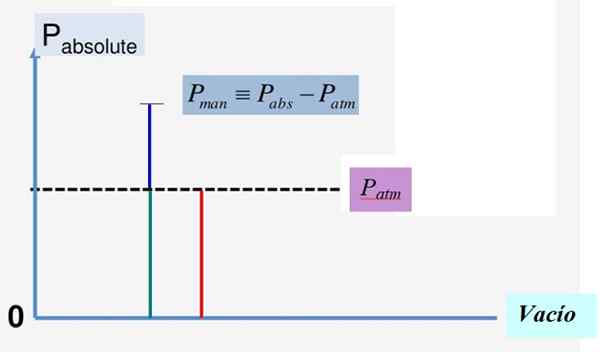
Gambar 1. Tekanan absolut dan tekanan manometrik. Sumber: f. Zapata.

Hubungan matematika antara ketiga kuantitas ini adalah:

P_ke = P_ATM + P_M

Karena itu:

P_M = P_ke - P_ATM

Gambar 1 dengan mudah menggambarkan hubungan ini. Karena tekanan vakum adalah 0, tekanan absolut selalu positif dan hal yang sama berlaku untuk tekanan atmosfer p_ATM.

Tekanan manometrik biasanya digunakan untuk menunjukkan tekanan di atas tekanan atmosfer, seperti yang dibawa oleh ban atau yang ada di bagian bawah laut atau kolam, yang diberikan oleh berat kolom air. Dalam kasus ini p_M > 0, karena p_ke > P_ATM.

Namun, ada tekanan mutlak di bawah P_ATM. Dalam kasus ini p_M < 0 y recibe el nombre de tekanan vakum Dan itu tidak boleh disamakan dengan tekanan vakum yang sudah dijelaskan, yaitu tidak adanya partikel yang mampu mengerahkan tekanan.

[TOC]

Rumus dan Persamaan

Tekanan dalam cairan -liquid atau gas -adalah salah satu variabel paling signifikan dalam studinya. Dalam cairan stasioner, tekanannya sama di semua titik ke kedalaman yang sama terlepas dari orientasi, sedangkan pergerakan cairan dalam pipa disebabkan oleh perubahan tekanan.

Tekanan rata -rata didefinisikan sebagai hasil bagi antara gaya tegak lurus terhadap permukaan F_⊥ dan area permukaan A tersebut, yang diekspresikan secara matematis sebagai berikut:

P = f_⊥ /KE

Tekanan adalah kuantitas skalar, yang dimensinya berkekuatan per unit area. Unit ukuran Anda dalam Sistem Unit Internasional (SI) adalah Newton/m², Disebut Pascal dan disingkat PA, untuk menghormati Blaise Pascal (1623-1662).

Kelipatan suka kilo (10³) Dan mega (10⁶) Mereka sering digunakan, karena tekanan atmosfer biasanya dalam kisaran 90.000 - 102.000 pa, yang sama dengan: 90 - 102 kPa. Tekanan urutan mega pascal tidak jarang, jadi penting untuk membiasakan diri dengan awalan.

Di unit Anglo -Saxon tekanan diukur dalam pound/kaki², Namun, hal umum harus dilakukan dalam pound/inci² salah satu psi (Pound-force per inci persegi).

Dapat melayani Anda: perpindahan panas: hukum, formulir transmisi, contoh

Variasi tekanan dengan kedalaman

Semakin kita membenamkan diri di dalam air kolam atau di laut, semakin banyak tekanan yang kita alami. Sebaliknya, meningkat tinggi, tekanan atmosfer berkurang.

Tekanan atmosfer rata -rata di permukaan laut ditetapkan pada 101300 PA atau 101.3 kPa, saat berada di lubang Mariana di Pasifik Barat - kedalaman terbesar yang diketahui - sekitar 1000 kali lebih tinggi dan di atas Everest hanya 34 kPa.

Jelas bahwa tekanan dan kedalaman (atau tinggi) terkait. Untuk mengetahui dalam kasus cairan istirahat (keseimbangan statis) itu dianggap sebagai bagian cairan dengan cairan berbentuk disk, terbatas dalam wadah, (lihat Gambar 2). Disk memiliki penampang KE, berat Dw dan tinggi Dy.

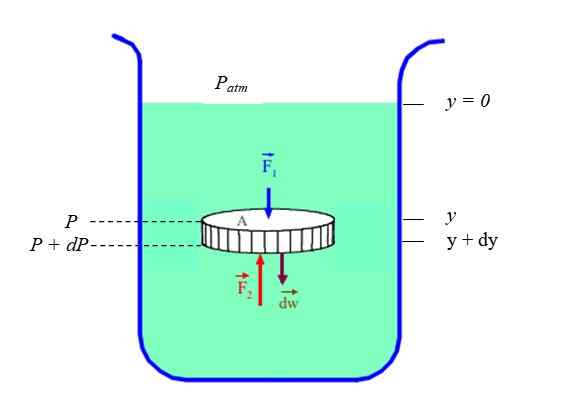Gambar 2. Elemen diferensial dari cairan keseimbangan statis. Sumber: Fanny Zapata.

Kami akan menelepon P pada tekanan yang ada secara mendalam "Dan" Dan P + DP pada tekanan yang ada secara mendalam (dan + dy). Karena kepadatan ρ dari cairan adalah alasan antara massanya DM dan volumenya Dv, Kamu harus:

ρ = DM/ DV ⇒ dm = ρ.Dv

Oleh karena itu beratnya Dw elemennya adalah:

DW = g. Dm = ρ.G.Dv

Dan sekarang hukum kedua Newton berlaku:

Σ f_Dan = F₂ - F₁ - DW = 0

(P + DP).A - p.KE - ρ.G.DV = 0

(P + DP).A - p.KE - ρ.G. KE. Dy = 0

Dp = ρ.G.Dy

Solusi persamaan diferensial 

Mengintegrasikan kedua belah pihak dan mempertimbangkan kepadatan itu ρ, serta gravitasi G Mereka konstan, ada ekspresi yang dicari:

P₂ - P₁ = ΔP = ρ.G.(Dan₂ - Dan₁)

ΔP = ρ.G. ΔDan

Jika dalam ekspresi sebelumnya dipilih P₁ seperti tekanan atmosfer dan Dan₁ Seperti permukaan cairan, lalu Dan₂ Terletak di kedalaman H Dan ΔP = p₂ - P_ATM Itu adalah tekanan manometrik tergantung pada kedalaman:

P_M = ρ.G.H

Jika Anda membutuhkan nilai tekanan absolut, tekanan atmosfer hanya ditambahkan ke hasil sebelumnya.

Contoh

Untuk pengukuran tekanan manometrik, perangkat digunakan pengukur tekanan, yang umumnya menawarkan perbedaan tekanan. Pada akhirnya, prinsip pengoperasian manometer tekanan U - -arpared akan dijelaskan, tetapi sekarang mari kita lihat beberapa contoh dan konsekuensi penting dari persamaan yang sebelumnya dikurangkan.

Prinsip Pascal

Persamaannya ΔP = ρ.G.(Dan₂ - Dan₁) Itu bisa ditulis sebagai  P = PO + ρ.G.H, Di mana P adalah tekanan di kedalaman H, ketika P_{salah satu} Itu adalah tekanan pada permukaan fluida, biasanya P_ATM.

Jelas setiap kali Anda meningkat PO, meningkat P dalam jumlah yang sama, selama itu adalah cairan yang kepadatannya konstan. Justru apa yang seharusnya dipertimbangkan ρ konstan dan tempatkan di luar integral diselesaikan di bagian sebelumnya.

Dapat melayani Anda: gerakan harmonik sederhana

Prinsip Pascal menyatakan bahwa setiap peningkatan tekanan cairan yang dibatasi dalam kesetimbangan, ditransmisikan tanpa variasi ke semua titik cairan tersebut. Melalui properti ini, dimungkinkan untuk melipatgandakan kekuatan F₁ diterapkan di kiri kecil kiri, dan dapatkan F₂ di kanan.

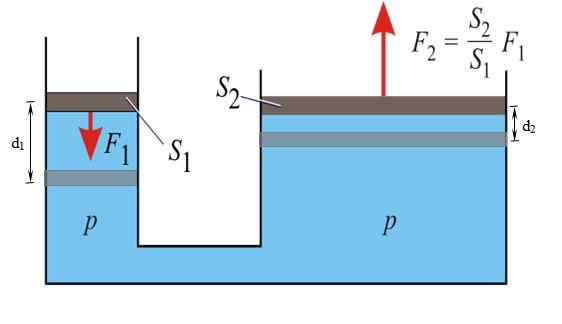Gambar 3. Dalam pers hidrolik prinsip pascal diterapkan. Sumber: Wikimedia Commons.

Rem mobil bekerja di bawah prinsip ini: gaya yang relatif kecil diterapkan pada pedal, yang menjadi kekuatan utama pada silinder rem pada setiap roda, berkat cairan yang digunakan dalam sistem.

Paradoks Hidrostatik Stevin

Paradoks hidrostatik menyatakan bahwa gaya karena tekanan cairan di bagian bawah wadah dapat sama, lebih besar atau lebih kecil dari berat cairan itu sendiri. Tetapi ketika meletakkan wadah di atas skala, biasanya akan mencatat berat cairan (ditambah satu wadah tentu saja). Bagaimana menjelaskan paradoks ini?

Kami mulai dari fakta bahwa tekanan di bagian bawah wadah tergantung secara eksklusif pada kedalaman dan tidak tergantung pada formulir, sebagaimana disimpulkan di bagian sebelumnya.

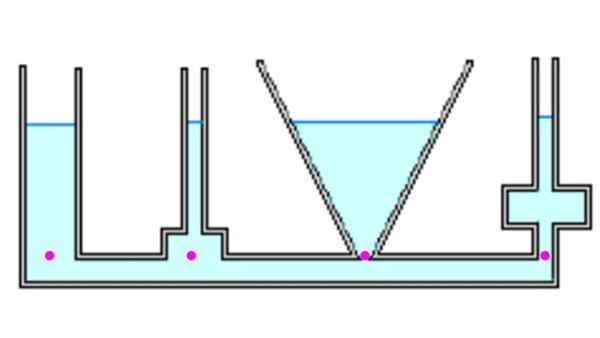Gambar 4. Cairan mencapai ketinggian yang sama di semua wadah dan tekanan di latar belakang adalah sama. Sumber: f. Zapata.

Mari kita lihat beberapa wadah yang berbeda. Saat dikomunikasikan, ketika mereka dipenuhi dengan cairan, semua orang mencapai ketinggian yang sama H. Poin -poin terkemuka berada pada tekanan yang sama, karena mereka berada pada kedalaman yang sama. Namun, gaya karena tekanan pada setiap titik dapat berbeda dari berat, (lihat Contoh 1 di bawah).

Latihan

Latihan 1

Bandingkan gaya yang diberikan dengan tekanan di bagian bawah masing -masing wadah dengan berat cairan, dan jelaskan mengapa perbedaannya, jika ada.

Wadah 1 

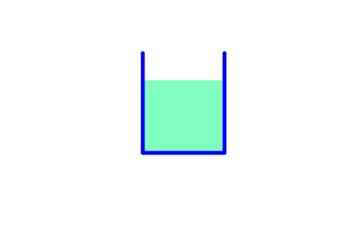Gambar 5. Tekanan di latar belakang sama besarnya dengan berat cairan. Sumber: Fanny Zapata.

Dalam wadah ini, area dasar adalah, oleh karena itu:

Berat Fluida: Mg = ρ.V.G = ρ . KE .H . G

Tekanan di bagian bawah: ρ. G. H

Kekuatan karena tekanan: f = p.A = ρ. G. H. KE

Berat dan gaya karena tekanannya sama.

Wadah 2 

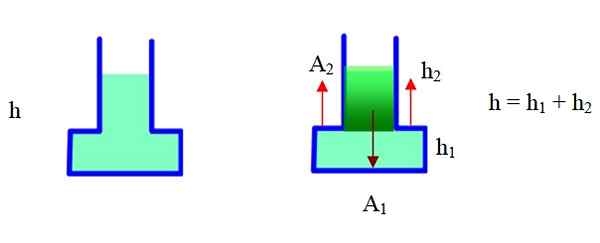Gambar 6. Gaya karena tekanan dalam wadah ini lebih besar dari berat. Sumber: f. Zapata.

Wadah memiliki bagian yang sempit dan bagian yang luas. Dalam skema yang tepat telah dibagi menjadi dua bagian dan akan menggunakan geometri untuk menemukan volume total. Area a₂ adalah eksternal dari wadah, h₂ Itu adalah ketinggian bagian sempit, h₁ Itu adalah ketinggian bagian lebar (dasar).

Dapat melayani Anda: Pleiades: Sejarah, Asal dan Komposisi

Volume lengkap adalah volume dasar + volume bagian sempit. Dengan data yang Anda miliki:

Berat Fluida: M . G = ρ . G. V = ρ . G. [KE₁ .H₁+ (KE₁ -KE₂) .H₂] =

= ρ . g (a₁.Ha₂H₂) = ρ . G . KE₁.H - ρ . G . KE._. H₂ (Penggunaan h = h₁ +H₂)

Tekanan di bagian bawah: p = ρ. G. H

Kekuatan di bagian bawah karena tekanan: f = p. KE₁ = ρ. G. H. KE₁

Membandingkan berat fluida dengan gaya karena tekanan dicatat bahwa ini lebih besar dari berat.

Apa yang terjadi adalah bahwa cairan juga memberikan kekuatan pada bagian langkah dalam wadah (lihat panah merah gambar) yang termasuk dalam perhitungan sebelumnya. Kekuatan tunangan ini untuk yang diberikan ke bawah dan berat yang dicatat oleh skala adalah hasil dari ini. Menurut ini, besarnya beratnya adalah:

W = gaya pada latar belakang - Kekuatan pada bagian terhuyung = ρ . G . KE₁.H - ρ . G . KE._. H₂

Latihan 2

Gambar tersebut menunjukkan pengukur tekanan tabung terbuka. Ini terdiri dari tabung U, di mana salah satu ujungnya berada pada tekanan atmosfer dan yang lain terhubung ke S, sistem yang tekanannya akan diukur.

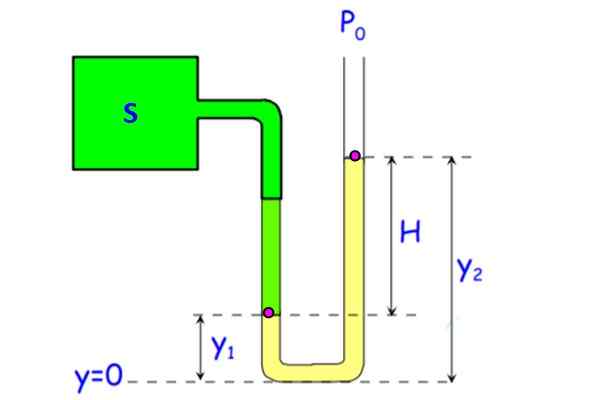Gambar 7. Buka tabung pengukur tekanan. Sumber: f. Zapata.

Cairan dalam tabung (berwarna kuning pada gambar) dapat berupa air, meskipun merkuri digunakan untuk mengurangi ukuran perangkat. (Perbedaan 1 atmosfer atau 101.3 kPa membutuhkan 10 kolom air.3 meter, tidak ada portabel).

Itu diminta untuk menemukan tekanan manometrik P_M Dalam sistem S, tergantung pada tinggi h kolom cairan.

Larutan

Tekanan di latar belakang untuk kedua cabang tabung adalah sama, untuk berada di kedalaman yang sama. Biarkan hal_KE Tekanan pada titik A, terletak di dan₁ Dan p_B Titik B yang berada di ketinggian dan₂. Karena titik B terletak di antarmuka cairan dan udara, tekanan ada p_{salah satu}. Di cabang pengukur tekanan ini, tekanan di bagian bawah adalah:

PO + ρ.G.Dan₂

Untuk bagiannya, tekanan di bagian bawah untuk cabang kiri adalah:

P + ρ.G.Dan₁

Di mana P adalah tekanan absolut dari sistem dan ρ adalah kepadatan cairan. Sama dengan kedua tekanan:

PO + ρ.G.Dan₂ = P +ρ.G.Dan₁

Membersihkan P:

P = PO + ρ.G.Dan₂ - ρ.G.Dan₁ = PO + ρ.G (dan₂ - Dan₁) = Po + ρ.G. H

Oleh karena itu, tekanan manometrik P_M Itu diberikan oleh P - p_{salah satu} = ρ.G. H Dan untuk memiliki nilainya, itu cukup untuk mengukur ketinggian di mana cairan manometrik naik dan melipatgandakannya dengan nilai G dan kepadatan cairan.

Referensi

1. Cimbala, c. 2006. Mekanika Cairan, Fundamental dan Aplikasi. MC. Bukit Graw. 66-74.
2. Figueroa, d. 2005. Seri: Fisika untuk Sains dan Teknik. Volume 4. Cairan dan termodinamika. Diedit oleh Douglas Figueroa (USB). 3-25.
3. Mott, r. 2006. Mekanika Cairan. 4. Edisi. Pendidikan Pearson. 53-70.
4. Shaugnessy, e. 2005. Pengantar Mekanika Cairan.Oxford University Press. 51 - 60.
5. Stylianos, v. 2016. Untuk penjelasan sederhana tentang paradoks hidrostatik klasik. Pulih dari: haimgaifman.File.WordPress.com