Sepupu relatif apa itu, penjelasan, contoh

Disebut sepupu relatif (Coprmimos atau sepupu relatif satu sama lain) terhadap setiap pasangan bilangan bulat yang tidak memiliki pembagi yang umum, kecuali 1. Dengan kata lain, dua bilangan bulat adalah sepupu relatif jika dalam kerusakan dalam bilangan prima, mereka tidak memiliki faktor umum.

Misalnya, jika 4 dan 25 dipilih, dekomposisi pada faktor utama masing -masing adalah 2² dan 5² masing -masing. Seperti yang dapat dilihat, mereka tidak memiliki faktor umum, oleh karena itu, 4 dan 25 adalah sepupu relatif.

Di sisi lain, jika Anda memilih 6 dan 24, saat membuat kerusakan pada faktor utama, diperoleh bahwa 6 = 2*3 dan 24 = 2³*3.

Seperti dapat dilihat, dua ekspresi terakhir ini memiliki setidaknya satu faktor umum, oleh karena itu, mereka bukan sepupu relatif.

Karakteristik sepupu relatif

Detail dengan perawatan mana.

Di sisi lain, definisi di atas dapat diringkas sebagai berikut: dua bilangan bulat "A" dan "B" adalah sepupu relatif jika, dan hanya, pembagi umum maksimum ini adalah 1, yaitu, MCD (A, B, ) = 1.

Dua kesimpulan langsung dari definisi ini adalah bahwa:

-Jika "a" (atau "b") adalah bilangan prima, maka mcd (a, b) = 1.

-Jika "a" dan "b" adalah bilangan prima, maka mcd (a, b) = 1.

Yaitu, jika setidaknya satu dari angka yang dipilih adalah bilangan prima, maka pasangan angka adalah sepupu relatif.

Fitur lainnya

Hasil lain yang digunakan untuk menentukan apakah dua angka adalah sepupu relatif adalah:

-Jika dua bilangan bulat berturut -turut, maka ini adalah sepupu relatif.

-Dua bilangan alami "A" dan "B" adalah sepupu relatif jika, dan hanya jika, angka "(2^a) -1" dan "(2^b) -1" adalah sepupu relatif.

-Dua bilangan bulat "A" dan "B" adalah sepupu relatif jika, dan hanya jika, saat memberi grafik titik (a, b) di bidang Cartesian, dan membangun garis yang melewati asal (0,0) dan (a , b), ini tidak mengandung titik apa pun dengan seluruh koordinat.

Contoh

1.- Pertimbangkan bilangan bulat 5 dan 12. Dekomposisi dalam faktor utama dari kedua angka adalah: masing -masing: 5 dan 2²*3. Kesimpulannya, MCD (5,12) = 1, oleh karena itu, 5 dan 12 adalah sepupu relatif.

2.- Biarkan angka -4 dan 6. Kemudian -4 = -2² dan 6 = 2*3, sehingga mcd (-4,6) = 2 ≠ 1. Kesimpulan -4 dan 6 bukan sepupu relatif.

Jika garis yang melewati pasangan yang dipesan (-4,6) dan (0,0), dan untuk menentukan persamaan garis tersebut, dapat diverifikasi bahwa ini melewati titik (-2,3).

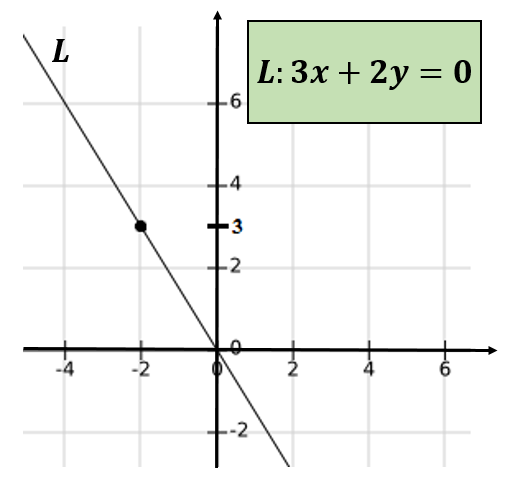
Sekali lagi, disimpulkan bahwa -4 dan 6 bukan sepupu relatif.

3.- Bilangan 7 dan 44 adalah sepupu relatif dan dapat disimpulkan dengan cepat berkat apa yang telah dikatakan di atas, karena 7 adalah bilangan prima.

4.- Pertimbangkan angka 345 dan 346. Menjadi dua angka berturut -turut, diverifikasi bahwa MCD (345.346) = 1, oleh karena itu, 345 dan 346 adalah sepupu relatif.

5.- Jika angka 147 dan 74 dipertimbangkan, maka ini adalah sepupu relatif, karena 147 = 3*7² dan 74 = 2*37, oleh karena itu, MCD (147,74) = 1.

6.- Angka 4 dan 9 adalah sepupu relatif. Untuk menunjukkannya, Anda dapat menggunakan karakterisasi kedua yang disebutkan di atas. Memang, 2^4 -1 = 16-1 = 15 dan 2^9-1 = 512-1 = 511.

Angka yang diperoleh adalah 15 dan 511. Dekomposisi dalam faktor utama dari angka -angka ini masing -masing adalah 3*5 dan 7*73, sehingga MCD (15.511) = 1.

Seperti yang Anda lihat, menggunakan karakterisasi kedua adalah pekerjaan yang lebih lama dan lebih melelahkan untuk memverifikasi secara langsung.

7.- Pertimbangkan angka -22 dan -27. Maka angka -angka ini dapat ditulis ulang sebagai berikut: -22 = -2*11 dan -27 = -3³. Oleh karena itu, MCD (-22, -27) = 1, jadi -22 dan -27 adalah sepupu relatif.