Produk silang

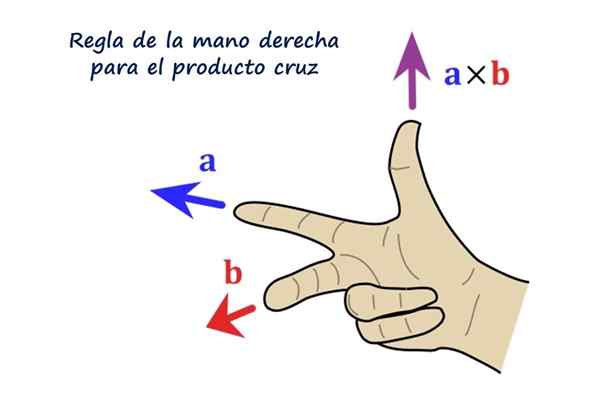Aturan yang tepat untuk produk vektor. Sumber: f. Zapata.

Apa produk silang atau produk vektor?

Dia Produk silang, Juga disebut produk vektor, ini adalah jenis produk yang dilakukan antara dua vektor dan menghasilkan vektor lain, tegak lurus terhadap bidang yang ditentukan oleh dua yang pertama.

Produk silang antara dua vektor ke Dan B, Itu menghasilkan vektor lain R, Secara matematis ditulis sebagai berikut:

ke × B = R

Bunyinya seperti ini: “A cruz b setara dengan r ".

Dalam teks yang dicetak, vektor ditulis dengan lirik yang berani, atau dengan panah pada surat itu, untuk membedakannya dari besarnya atau modulnya. Untuk ini mereka digunakan, secara bergantian, bilah modul dan huruf saat ini, sehingga nilai absolut dari vektor ke Simbol ditulis seperti ini:

│ke│ = a

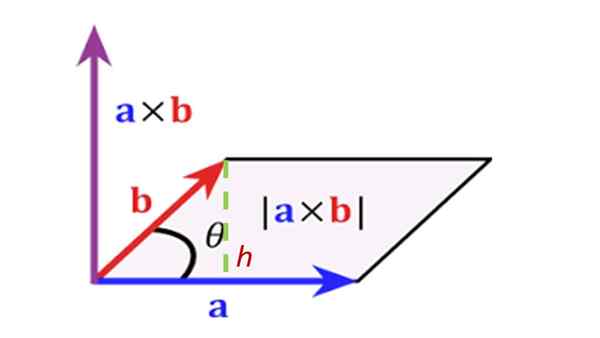
Nilai atau modul absolut dari produk vektor antara dua vektor dihitung dengan mengalikan modul kedua vektor melalui sudut θ di antara mereka:

R = a ∙ b ∙ sen θ

Arah vektor R Itu tegak lurus dengan vektor ke Dan B. Pengertian R Itu adalah dekstrogyr ke ke arah B Dan dalam praktiknya ditentukan menggunakan aturan tangan kanan, yang terdiri dari memposisikan indeks, sedang dan jempol tangan kanan sebagai berikut:

• Jari telunjuk ditempatkan mengikuti vektor ke
• Dengan jari tengah mengikuti vektor B
• Ibu jari, diperpanjang, menunjukkan arah dan arah vektor R.

Pesanan ini harus diikuti dengan tepat, karena produk vektor tidak komutatif, yaitu ke × B ≠ B × ke Dan jika vektor dipertukarkan, hasil yang benar tidak akan diperoleh.

Dapat melayani Anda: Teorema Keberadaan dan Keunikan: Demonstrasi, Contoh dan Latihan

Pembaca disarankan untuk menempatkan tangan kanannya seperti yang ditunjukkan gambar, indeks yang menunjuk ke kiri mewakili vektor ke, Jari tengah mengikuti B Dan itu menunjuk langsung ke pembaca, akhirnya, ibu jari menunjukkan ke atas, menunjuk ke arah dan arah vektor ke × B = R.

Properti Produk Cruz

-Produk salib atau vektor antara dua vektor selalu menghasilkan vektor lain.

-Oleh karena itu, produk silang tidak melakukan komutatif: ke × B ≠ B × ke.

-Untuk produk silang memang benar bahwa: ke × B = - (B × ke). Properti ini dipanggil Anti-Konminasi.

-Vektor yang dihasilkan dari produk vektor antara dua vektor tegak lurus (normal) dengan vektor tersebut.

-Dari atas, ia mengikuti bahwa produk vektor antara vektor dengan arah yang sama adalah nol. Secara khusus ke × A = 0.

-Produk silang sesuai dengan undang -undang distribusi sehubungan dengan jumlah: ke × (B+C) = ke × B + ke × C

-Jika m adalah skalar, maka m (ke × B) = m ke × B = ke × m B

Produk silang antar vektor unit

Tiga unit vektor, disebut yo, J Dan k, Mereka saling tegak lurus dan menunjukkan tiga arah ruang yang terkenal: tinggi, lebar dan dalam. Alamat ini saling tegak lurus.

Produk vektor antara vektor unit mudah ditentukan melalui aturan kanan dan mengingat sifat -sifat produk silang:

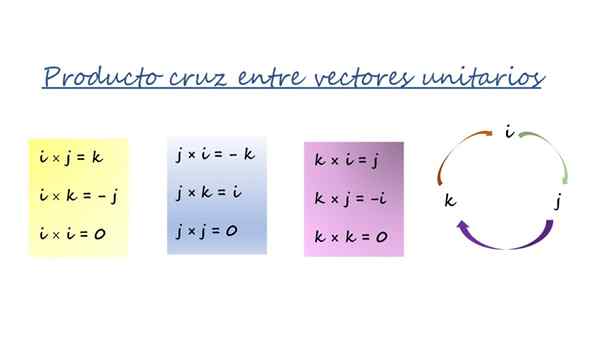Produk vektor vektor unit cartesian. Sumber: f. Zapata.

Tiga kotak berwarna pada gambar dirangkum dalam putaran dengan panah di sebelah kanan dan digunakan dengan cara ini:

-Saat mengalikan arah panah, hasilnya adalah vektor di depan panah dan memiliki tanda positif. Misalnya, dengan mengalikan dengan vektor J Dan k, Vektor ketiga adalah yo, Dan karena perintah mengikuti arti panah, tandanya adalah +.

Dapat melayani Anda: fungsi vektor

-Dan jika dikalikan ke arah yang berlawanan dengan panah, hasilnya adalah vektor ketiga di depan panah, tetapi dengan tanda negatif.

Vektor unit merupakan basis, sehingga vektor lain dapat ditulis dalam hal mereka. Ini sangat memfasilitasi perhitungan produk silang antara dua vektor sewenang -wenang di luar angkasa.

Bagaimana menganalisis produk silang dari dua vektor secara analitik

Saat vektor ke Dan B Mereka memiliki arah sewenang -wenang di ruang angkasa, dengan komponen di sepanjang mereka, lebih mudah untuk menghitung produk silang dengan cara analitis, mengekspresikannya dalam hal vektor unit yo, J Dan k:

• ke = a_X yo + ke_Dan J + ke_z k
• B = b_X yo + B_Dan J + B_z k

Sekarang properti distributif perkalian digunakan, yang juga berlaku untuk produk silang:

ke × B = (a_X yo + ke_Dan J + ke_z k) × (b_X yo + B_Dan J + B_z k) =

= (a_X yo × b_X yo) + (a_X yo × b_Dan J) + (a_X yo × b_z k) + (a_DAN J × b_X yo) + (a_DAN J × b_Dan J) + (a_DAN J × b_z k) + (a_Z k × b_X yo) + (a_Z k × b_Dan J) + (a_Z k × b_z k)

Produk silang antara vektor unit yang sama dibatalkan, karena mereka adalah vektor paralel, yang mengurangi ekspresi ini menjadi 6 istilah:

ke × B = (a_X yo × b_Dan J) + (a_X yo × b_z k) + (a_DAN J × b_X yo) + (a_DAN J × b_z k) + (a_Z k × b_X yo) + (a_Z k × b_Dan J)

Akhirnya, menggunakan gambar di atas, setiap produk menghasilkan:

ke × B = a_X B_Dan k + ke_X B_z ( -J) + a_DAN B_X ( -k) + a_DAN B_z yo + ke_Z B_XJ + ke_Z B_Dan ( -yo) =

= (a_DAN B_z - A_Z B_Dan) yo + (ke_Z B_X - A_X B_z) J + (ke_X B_Dan - A_DAN B_X) k

Produk Cruz melalui penentu

Tidak perlu menghafal rumus di atas, tetapi dengan mudah menerapkan putaran sosok sebelumnya atau dengan hati -hati melaksanakan penentu yang ditunjukkan di bawah ini, yang sepenuhnya setara:

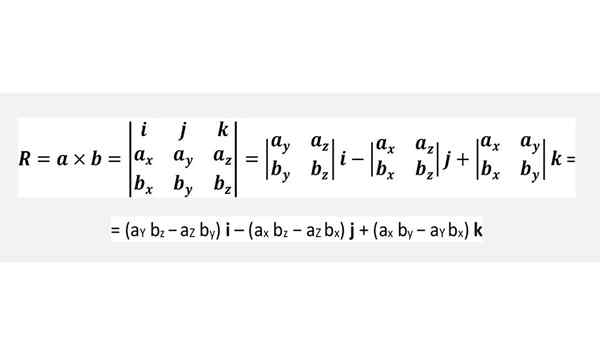
Contoh

Dengan asumsi vektor ke Dan B adalah:

• ke = 5 yo - J + 4 k
• B = -yo + 0J +7 k

Produk silang di antara mereka dihitung dengan mengidentifikasi dan mengganti koordinat masing -masing:

Dapat melayani Anda: paraboloid hiperbolik: definisi, sifat, dan contoh

ke_X = 5; ke_Dan = −1; ke_z = 4; B_X = −1; B_Dan = 0: b_z = 7

ke × B = [(−1) ∙ 7 - 4 ∙ 0] yo + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] yo + [(−4 - 35) J + [0 - 1] k =

= (−7) yo - 39 J - k

Metode penentu menawarkan hasil yang sama.

Latihan

Hitung dengan penentu, produk silang di antara vektor:

• atau = 2 yo +J + 5 k
• v = yo + 4J +7 k

Dan tentukan area jajaran genjang yang digantikan oleh vektor sebelumnya, seperti yang ditunjukkan pada gambar:

Larutan

Nilai koordinat vektor diganti dalam penentu:

Area jajaran genjang yang ditentukan adalah modul produk vektor di antara mereka, yang dihasilkan: r = 17.3 unit area.