Bukti Properti Properti, Contoh

Itu Properti Kunci Aljabar Ini adalah fenomena yang menghubungkan dua elemen set dengan operasi, di mana kondisi yang diperlukan adalah, setelah 2 elemen di bawah operasi tersebut, hasilnya juga milik set awal.

Misalnya, jika angka genap diambil secara keseluruhan dan jumlah sebagai operasi, kunci set tersebut sehubungan dengan jumlah yang diperoleh. Ini karena jumlah 2 angka genap akan selalu diberikan sebagai hasilnya nomor lain, sehingga memenuhi kondisi kunci.

Sumber: Buka purba.com

[TOC]

Karakteristik

Ada banyak sifat yang menentukan ruang atau tubuh aljabar, seperti struktur atau cincin. Namun, properti kunci adalah salah satu yang paling terkenal dalam aljabar dasar.

Tidak semua aplikasi dari sifat -sifat ini didasarkan pada fenomena atau elemen numerik. Banyak contoh sehari-hari dapat bekerja dari pendekatan aljabar-teoretis murni.

Contohnya dapat menjadi warga negara dari suatu negara yang mengambil hubungan hukum dalam bentuk apa pun, seperti masyarakat komersial atau perkawinan antara lain. Setelah operasi atau manajemen ini, mereka masih warga negara. Dengan demikian, kewarganegaraan dan operasi manajemen sehubungan dengan dua warga negara mewakili kunci.

Aljabar numerik

Sehubungan dengan angka, ada banyak aspek yang telah menjadi alasan untuk belajar dalam berbagai arus matematika dan aljabar. Dari studi ini, sejumlah besar aksioma dan teorema telah muncul yang berfungsi sebagai dasar teoritis penelitian dan karya kontemporer.

Jika Anda bekerja dengan set numerik, kami dapat menetapkan definisi lain yang valid untuk properti kunci. Dikatakan bahwa satu set A adalah kunci dari set B lain jika A adalah set terkecil yang berisi semua set dan operasi yang House B b.

Dapat melayani Anda: properti distributif

Demonstrasi

Demonstrasi kunci diterapkan pada elemen dan operasi yang ada dalam set angka N nyata.

Misalkan A dan B menjadi dua angka milik set R, kunci elemen -elemen ini didefinisikan untuk setiap operasi yang terkandung dalam R.

Tambahan

- Jumlah: ∀ A ˄ B ∈ R → A + B = C ∈ R

Ini adalah cara aljabar untuk mengatakan itu Untuk semua A dan B milik bilangan real, itu harus menjadi jumlah lebih B adalah sama dengan C, yang juga milik yang nyata.

Mudah untuk memeriksa apakah proposisi ini benar; Itu cukup untuk membuat jumlah antara bilangan real apa pun dan memverifikasi jika hasilnya juga milik bilangan real.

3 + 2 = 5 ∈ R

-2 + (-7) = -9 ∈ R

-3 + 1/3 = -8/3 ∈ R

5/2 + (-2/3) = 11/6 ∈ R

Diamati bahwa kondisi kunci dipenuhi untuk bilangan real dan jumlahnya. Dengan cara ini dapat disimpulkan: Jumlah bilangan real adalah kunci aljabar.

Perkalian

- Multiplikasi: ∀ A ˄ B ∈ R → A . B = c ∈ R

Untuk semua A dan B yang termasuk yang asli, penggandaan A untuk B sama dengan C, yang juga milik yang asli.

Saat memverifikasi dengan elemen yang sama dari contoh sebelumnya, hasil berikut diamati.

3 x 2 = 6 ∈ R

-2 x (-7) = 14 ∈ R

-3 x 1/3 = -1 ∈ R

5/2 x (-2/3) = -5/3 ∈ R

Ini adalah bukti yang cukup untuk menyimpulkan bahwa: Penggandaan bilangan real adalah kunci aljabar.

Definisi ini dapat diperluas ke semua operasi bilangan real, meskipun kami akan menemukan pengecualian tertentu.

Sumber: Pixabay.com

Kasus Khusus di R

Divisi

Sebagai kasus khusus, divisi ini diamati, di mana pengecualian berikut dihargai:

Dapat melayani Anda: probabilitas klasik: perhitungan, contoh, latihan terpecahkan

∀ A ˄ B ∈ R → A / B ∉ R ↔ B = 0

Untuk semua A dan B yang menjadi milik R Itu harus antara b bukan milik reais jika dan hanya jika b sama dengan nol.

Kasus ini mengacu pada pembatasan tidak dapat membagi antara nol. Karena nol milik bilangan real, maka disimpulkan bahwa: lDivisi bukanlah kunci nyata.

Radio

Ada juga operasi potensiasi, lebih khusus pengarsipan, di mana pengecualian disajikan untuk kekuatan radikal indeks torsi:

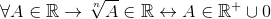; Dengan n par

Untuk segala sesuatu yang menjadi milik kerajaan.

Dengan cara ini dinyatakan bahwa akar genap hanya berlaku untuk yang nyata yang nyata dan disimpulkan bahwa potensiasi bukanlah kunci di R.

Logaritma

Disetujui untuk fungsi logaritmik, yang tidak didefinisikan untuk nilai yang lebih kecil atau sama dengan nol. Untuk memeriksa apakah logaritma adalah kunci R

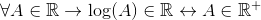
Untuk segala sesuatu yang menjadi milik Reais, logaritma A milik Reais, jika dan hanya jika itu milik nyata yang positif.

Ketika nilai negatif dan nol yang juga termasuk R dikecualikan, dapat ditegaskan bahwa:

Logaritma bukanlah kunci bilangan real.

Contoh

Periksa kunci untuk jumlah dan pengurangan bilangan alami:

Jumlah dalam n

Hal pertama adalah memeriksa kondisi kunci untuk elemen yang berbeda dari set yang diberikan, di mana jika diamati bahwa beberapa elemen pecah dengan kondisi tersebut, keberadaan kunci dapat secara otomatis ditolak.

Dapat melayani Anda: Radio Konvergensi: Definisi, Contoh dan Latihan Diselesaikan

Properti ini dipenuhi untuk semua nilai yang mungkin dari A dan B, seperti yang diamati dalam operasi berikut:

1 + 3 = 4 ∈ N

5 + 7 = 12 ∈ N

1000 + 10000 = 11000 ∈ N

Tidak ada nilai alami yang memecahkan kondisi kunci, jadi disimpulkan:

Jumlahnya adalah kunci di n.

Kurangi di n

Unsur -unsur alami dicari yang mampu melanggar kondisi; A - B milik penduduk asli.

Beroperasi, mudah untuk menemukan pasangan elemen alami yang tidak memenuhi kondisi kunci. Misalnya:

7 - 10 = -3 ∉ A n

Dengan begitu kita bisa menyimpulkan bahwa:

Pengurangannya bukanlah kunci set bilangan alami.

Latihan yang diusulkan

1-SAMP.

2-Explain Jika himpunan bilangan real adalah kunci dari keseluruhan seluruh angka.

3-determine set numerik mana yang bisa menjadi kunci bilangan real.

4-sampel properti kunci untuk set angka imajiner, sehubungan dengan jumlah, pengurangan, perkalian dan pembagian dan pembagian.

Referensi

1. Panorama Matematika Murni: Pilihan Bourbakist. Jean Dieudonné. Reverte, 1987.
2. Teori Angka Aljabar. Alejandro J. Díaz Barriga, Ana Irene Ramírez, Francisco Tomás. National Autonomous University of Mexico, 1975.
3. Aljabar linier dan aplikasinya. Sandra Ibeth Ochoa García, Eduardo Gutiérrez González.
4. Struktur Aljabar V: Teori Tubuh. Héctor a. Merklen. Organisasi Negara Amerika, Sekretariat Umum, 1979.
5. Pengantar aljabar komutatif. Michael Francis Atiyah, I. G. MacDonald. Reverte, 1973.